| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
5.5 Multiple-Particle Systems Including Spin
Spin will turn out to have a major effect on how quantum particles
behave. Therefore, quantum mechanics as discussed so far must be
generalized to include spin. Just like there is a probability that a
particle is at some position  , there is the additional
probability that it has spin angular momentum
, there is the additional
probability that it has spin angular momentum 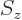 in an arbitrarily
chosen
in an arbitrarily
chosen  -direction and this must be included in the wave function.
This section discusses how.
-direction and this must be included in the wave function.
This section discusses how.
5.5.1 Wave function for a single particle with spin
The first question is how spin should be included in the wave function
of a single particle. If spin is ignored, a single particle has a
wave function 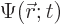 , depending on position
, depending on position  and on
time
and on
time 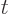 . Now, the spin
. Now, the spin 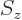 is just some other scalar
variable that describes the particle, in that respect no different
from say the
is just some other scalar
variable that describes the particle, in that respect no different
from say the  -position of the particle. The “every possible combination” idea of allowing every possible
combination of states to have its own probability indicates that
-position of the particle. The “every possible combination” idea of allowing every possible
combination of states to have its own probability indicates that 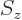 needs to be added to the list of variables. So the complete wave
function
needs to be added to the list of variables. So the complete wave
function 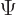 of the particle can be written out fully as:
of the particle can be written out fully as:
 |
(5.16) |
The value of 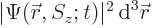 gives the probability of
finding the particle within a vicinity
gives the probability of
finding the particle within a vicinity 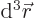 of
of  and with
spin angular momentum in the
and with
spin angular momentum in the  -direction
-direction 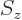 .
.
But note that there is a big difference between the spin
coordinate
and the position coordinates: while the
position variables can take on any value, the values of 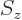 are
highly limited. In particular, for the electron, proton, and neutron,
are
highly limited. In particular, for the electron, proton, and neutron,
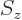 can only be
can only be 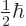 or
or 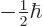 , nothing
else. You do not really have a full
, nothing
else. You do not really have a full 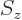
axis
, just
two points.
As a result, there are other meaningful ways of writing the wave
function. The full wave function 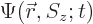 can be thought
of as consisting of two parts
can be thought
of as consisting of two parts 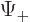 and
and 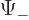 that only depend
on position:
that only depend
on position:
 |
(5.17) |
These two parts can in turn be thought of as being the components of a
two-dimensional vector that only depends on position:
Remarkably, Dirac found that the wave function for particles like
electrons has to be a vector, if it is assumed that the
relativistic equations take a guessed simple and beautiful form, like
the Schrödinger and all other basic equations of physics are simple and
beautiful. Just like relativity reveals that particles should have
build-in energy, it also reveals that particles like electrons have
build-in angular momentum. A description of the Dirac equation is in
chapter 12.12 if you are curious.
The two-dimensional vector is called a “spinor” to indicate that its components do not change like
those of ordinary physical vectors when the coordinate system is
rotated. (How they do change is of no importance here, but will
eventually be described in derivation {D.68}.) The spinor
can also be written in terms of a magnitude times a unit vector:
This book will just use the scalar wave function
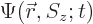 ; not a vector one. But it is often convenient
to write the scalar wave function in a form equivalent to the vector
one:
; not a vector one. But it is often convenient
to write the scalar wave function in a form equivalent to the vector
one:
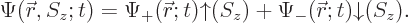 |
(5.18) |
The square magnitude of function 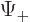 gives the probability of
finding the particle near a position with spin-up. That of
gives the probability of
finding the particle near a position with spin-up. That of 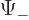 gives the probability of finding it with spin-down. The
gives the probability of finding it with spin-down. The
spin-up
function 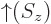 and the
and the
spin-down
function 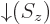 are in some sense the
equivalent of the unit vectors
are in some sense the
equivalent of the unit vectors 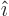 and
and 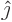 in normal vector
analysis; they have by definition the following values:
in normal vector
analysis; they have by definition the following values:
The function arguments will usually be left away for conciseness, so
that
is the way the wave function of, say, an electron will normally be
written out.
Key Points

- Spin must be included as an independent variable in the wave
function of a particle with spin.

- Usually, the wave function
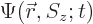 of a single
particle with spin
of a single
particle with spin 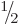 will be written as
will be written as
where 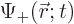 determines the probability of finding the
particle near a given location
determines the probability of finding the
particle near a given location  with spin up, and
with spin up, and
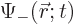 the one for finding it spin down.
the one for finding it spin down.

- The functions
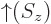 and
and 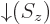 have the values
have the values
and represent the pure spin-up, respectively spin-down states.
5.5.1 Review Questions
-
1.
-
What is the normalization requirement of the wave function of a spin 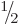 particle in terms of
particle in terms of 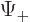 and
and 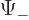 ?
?
Solution complexsa-a
5.5.2 Inner products including spin
Inner products are important: they are needed for finding
normalization factors, expectation values, uncertainty, approximate
ground states, etcetera. The additional spin coordinates add a new
twist, since there is no way to integrate over the few discrete points
on the spin axis
. Instead, you must sum over these
points.
As an example, the inner product of two arbitrary electron wave
functions 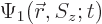 and
and 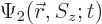 is
is
or writing out the two-term sum,
The individual factors in the integrals are by definition the spin-up
components 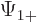 and
and 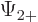 and the spin down components
and the spin down components
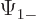 and
and 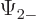 of the wave functions, so:
of the wave functions, so:
In other words, the inner product with spin evaluates as
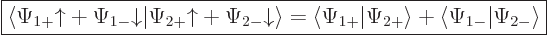 |
(5.19) |
It is spin-up components together and spin-down components together.
Another way of looking at this, or maybe remembering it, is to note
that the spin states are an orthonormal pair,
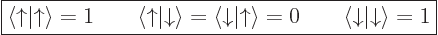 |
(5.20) |
as can be verified directly from the definitions of those functions as
given in the previous subsection. Then you can think of an inner
product with spin as multiplying out as:
Key Points

- In inner products, you must sum over the spin states.

- For spin
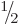 particles:
particles:
which is spin-up components together plus spin-down components together.

- The spin-up and spin-down states
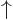 and
and 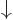 are an
orthonormal pair.
are an
orthonormal pair.
5.5.2 Review Questions
-
1.
-
Show that the normalization requirement for the wave function of a spin 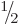 particle in terms of
particle in terms of 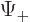 and
and 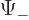 requires its norm
requires its norm 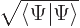 to be one.
to be one.
Solution complexsai-a
-
2.
-
Assume that 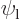 and
and 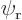 are normalized spatial wave functions. Now show that a combination of the two like
are normalized spatial wave functions. Now show that a combination of the two like 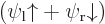

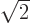 is a normalized wave function with spin.
is a normalized wave function with spin.
Solution complexsai-b
5.5.3 Commutators including spin
There is no known internal physical mechanism
that
gives rise to spin like there is for orbital angular momentum.
Fortunately, this lack of detailed information about spin is to a
considerable amount made less of an issue by knowledge about its
commutators.
In particular, physicists have concluded that spin components satisfy
the same commutation relations as the components of orbital angular
momentum:
![\begin{displaymath}
\fbox{$\displaystyle
[{\widehat S}_x,{\widehat S}_y] = {\r...
...idehat S}_z,{\widehat S}_x] = {\rm i}\hbar{\widehat S}_y
$} %
\end{displaymath}](img1029.gif) |
(5.21) |
These equations are called the “fundamental commutation
relations.” As will be shown in chapter 12, a
large amount of information about spin can be teased from them.
Further, spin operators commute with all functions of the spatial
coordinates and with all spatial operators, including position, linear
momentum, and orbital angular momentum. The reason why can be
understood from the given description of the wave function with spin.
First of all, the square spin operator 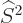 just multiplies the
entire wave function by the constant
just multiplies the
entire wave function by the constant 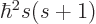 , and
everything commutes with a constant. And the operator
, and
everything commutes with a constant. And the operator 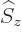 of spin
in an arbitrary
of spin
in an arbitrary  -direction commutes with spatial functions and
operators in much the same way that an operator like
-direction commutes with spatial functions and
operators in much the same way that an operator like
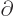

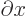 commutes with functions depending on
commutes with functions depending on  and
with
and
with 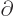

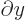 . The
. The  -component of spin
corresponds to an additional
-component of spin
corresponds to an additional axis
separate from the
 ,
,  , and
, and  ones, and
ones, and 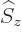 only affects the
variation in this additional direction. For example, for a particle
with spin one half,
only affects the
variation in this additional direction. For example, for a particle
with spin one half, 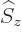 multiplies the spin-up part of the wave
function
multiplies the spin-up part of the wave
function 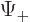 by the constant
by the constant 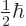 and
and 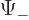 by
by
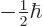 . Spatial functions and operators commute with
these constants for both
. Spatial functions and operators commute with
these constants for both 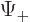 and
and 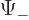 hence commute with
hence commute with
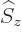 for the entire wave function. Since the
for the entire wave function. Since the  -direction is
arbitrary, this commutation applies for any spin component.
-direction is
arbitrary, this commutation applies for any spin component.
Key Points

- While a detailed mechanism of spin is missing, commutators with
spin can be evaluated.

- The components of spin satisfy the same mutual commutation
relations as the components of orbital angular momentum.

- Spin commutes with spatial functions and operators.
5.5.3 Review Questions
-
1.
-
Are not some commutators missing from the fundamental commutation relationship? For example, what is the commutator ![$[{\widehat S}_y,{\widehat S}_x]$](img1036.gif) ?
?
Solution complexsac-a
5.5.4 Wave function for multiple particles with spin
The extension of the ideas of the previous subsections towards multiple
particles is straightforward. For two particles, such as the two
electrons of the hydrogen molecule, the full wave function follows from
the every possible combination
idea as
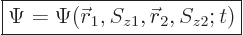 |
(5.22) |
The value of
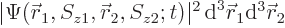 gives the
probability of simultaneously finding particle 1 within a vicinity
gives the
probability of simultaneously finding particle 1 within a vicinity
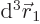 of
of 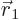 with spin angular momentum in the
with spin angular momentum in the
 -direction
-direction 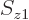 , and particle 2 within a vicinity
, and particle 2 within a vicinity
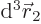 of
of 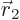 with spin angular momentum in the
with spin angular momentum in the
 -direction
-direction 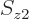 .
.
Restricting the attention again to spin 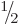 particles like
electrons, protons and neutrons, there are now four possible spin
states at any given point, with corresponding spatial wave functions
particles like
electrons, protons and neutrons, there are now four possible spin
states at any given point, with corresponding spatial wave functions
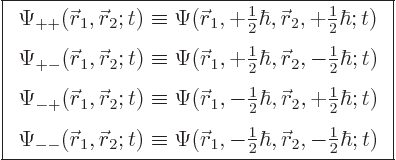 |
(5.23) |
For example, 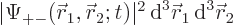 gives
the probability of finding particle 1 within a vicinity
gives
the probability of finding particle 1 within a vicinity 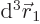 of
of
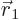 with spin up, and particle 2 within a vicinity
with spin up, and particle 2 within a vicinity 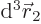 of
of
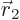 with spin down.
with spin down.
The wave function can be written using purely spatial functions and
purely spin functions as
As you might guess from this multi-line display, usually this will be
written more concisely as
by leaving out the arguments of the spatial and spin functions. The
understanding is that the first of each pair of arrows refers to
particle 1 and the second to particle 2.
The inner product now evaluates as
This can be written in terms of the purely spatial components as
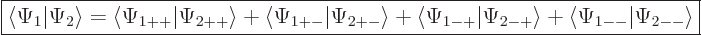 |
(5.24) |
It reflects the fact that the four spin basis states 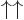 ,
,
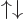 ,
, 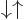 , and
, and 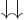 are an orthonormal
quartet.
are an orthonormal
quartet.
Key Points

- The wave function of a single particle with spin generalizes in a
straightforward way to multiple particles with spin.

- The wave function of two spin
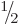 particles can be
written in terms of spatial components multiplying pure spin states
as
particles can be
written in terms of spatial components multiplying pure spin states
as
where the first arrow of each pair refers to particle 1 and the second
to particle 2.

- In terms of spatial components, the inner product
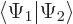 evaluates as inner products of
matching spin components:
evaluates as inner products of
matching spin components:

- The four spin basis states
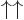 ,
, 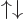 ,
,
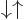 , and
, and 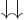 are an orthonormal quartet.
are an orthonormal quartet.
5.5.4 Review Questions
-
1.
-
As an example of the orthonormality of the two-particle spin states, verify that 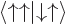 is zero, so that
is zero, so that 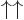 and
and 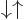 are indeed orthogonal. Do so by explicitly writing out the sums over
are indeed orthogonal. Do so by explicitly writing out the sums over 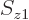 and
and 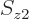 .
.
Solution complexsb-a
-
2.
-
A more concise way of understanding the orthonormality of the two-particle spin states is to note that an inner product like 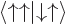 equals
equals 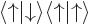 , where the first inner product refers to the spin states of particle 1 and the second to those of particle 2. The first inner product is zero because of the orthogonality of
, where the first inner product refers to the spin states of particle 1 and the second to those of particle 2. The first inner product is zero because of the orthogonality of 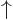 and
and 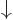 , making
, making 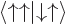 zero too.
zero too.
To check this argument, write out the sums over 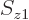 and
and 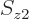 for
for 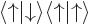 and verify that it is indeed the same as the written out sum for
and verify that it is indeed the same as the written out sum for 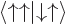 given in the answer for the previous question.
given in the answer for the previous question.
The underlying mathematical principle is that sums of products can be factored into separate sums as in:
This is similar to the observation in calculus that integrals of products can be factored into separate integrals:
Solution complexsb-b
5.5.5 Example: the hydrogen molecule
As an example, this section considers the ground state of the hydrogen
molecule. It was found in section 5.2 that the ground
state electron wave function must be of the approximate form
where 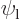 was the electron ground state of the left hydrogen
atom, and
was the electron ground state of the left hydrogen
atom, and 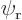 the one of the right one;
the one of the right one;  was just a
normalization constant. This solution excluded all consideration of
spin.
was just a
normalization constant. This solution excluded all consideration of
spin.
Including spin, the ground state wave function must be of the general
form
As you might guess, in the ground state, each of the four spatial
functions 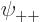 ,
, 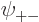 ,
, 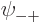 , and
, and
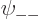 must be proportional to the no-spin solution
must be proportional to the no-spin solution
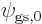 above. Anything else would have more than the
lowest possible energy, {D.24}.
above. Anything else would have more than the
lowest possible energy, {D.24}.
So the approximate ground state including spin must take the form
![\begin{displaymath}
\psi_{{\rm gs}} =
a
\left[
\psi_{\rm {l}}({\skew0\vec r}...
...downarrow}{\uparrow}+
a_{-}{\downarrow}{\downarrow}
\right]
\end{displaymath}](img1067.gif) |
(5.25) |
where 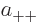 ,
, 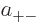 ,
, 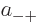 , and
, and  are
constants.
are
constants.
Key Points

- The electron wave function
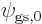 for the hydrogen
molecule derived previously ignored spin.
for the hydrogen
molecule derived previously ignored spin.

- In the full electron wave function, each spatial component must
separately be proportional to
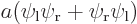 .
.
5.5.5 Review Questions
-
1.
-
Show that the normalization requirement for 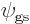 means that
means that
Solution complexsc-a
5.5.6 Triplet and singlet states
In the case of two particles with spin 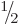 , it is often
more convenient to use slightly different basis states to describe the
spin states than the four arrow combinations
, it is often
more convenient to use slightly different basis states to describe the
spin states than the four arrow combinations 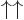 ,
,
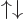 ,
, 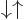 , and
, and 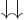 . The more
convenient basis states can be written in
. The more
convenient basis states can be written in 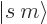 ket notation,
and they are:
ket notation,
and they are:
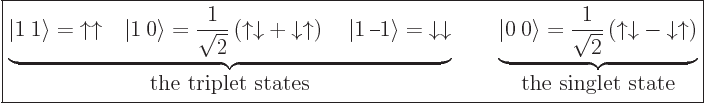 |
(5.26) |
A state 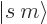 has net spin
has net spin 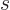 , giving a net square
angular momentum
, giving a net square
angular momentum 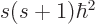 , and has net angular
momentum in the
, and has net angular
momentum in the  -direction
-direction 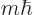 . For example, if
the two particles are in the state
. For example, if
the two particles are in the state 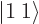 , the net square
angular momentum is
, the net square
angular momentum is 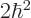 , and their net angular momentum
in the
, and their net angular momentum
in the  -direction is
-direction is  .
.
The 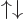 and
and 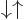 states can be written as
states can be written as
This shows that while they have zero angular momentum in the
 -direction; they do not have a value for the net spin: they have a 50/50
probability of net spin 1 and net spin 0. A consequence is that
-direction; they do not have a value for the net spin: they have a 50/50
probability of net spin 1 and net spin 0. A consequence is that
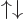 and
and 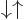 cannot be written in
cannot be written in 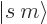 ket notation;
there is no value for
ket notation;
there is no value for 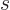 . (Related to that, these states also
do not have a definite value for the dot product of the two spins,
{A.10}.
. (Related to that, these states also
do not have a definite value for the dot product of the two spins,
{A.10}.
Incidentally, note that  components of angular momentum simply add
up, as the Newtonian analogy suggests. For example, for
components of angular momentum simply add
up, as the Newtonian analogy suggests. For example, for
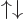 , the
, the 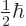 spin angular momentum of the first
electron adds to the
spin angular momentum of the first
electron adds to the 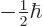 of the second electron to produce
zero. But Newtonian analysis does not allow square angular momenta to
be added together, and neither does quantum mechanics. In fact, it is
quite a messy exercise to actually prove that the triplet and singlet
states have the net spin values claimed above. (See chapter
12 if you want to see how it is done.)
of the second electron to produce
zero. But Newtonian analysis does not allow square angular momenta to
be added together, and neither does quantum mechanics. In fact, it is
quite a messy exercise to actually prove that the triplet and singlet
states have the net spin values claimed above. (See chapter
12 if you want to see how it is done.)
The spin states 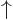

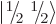 and
and 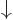

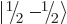 that
apply for a single spin-
that
apply for a single spin-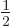 particle are often referred to as
the “doublet” states, since there are two of them.
particle are often referred to as
the “doublet” states, since there are two of them.
Key Points

- The set of spin states
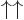 ,
, 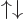 ,
,
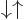 , and
, and 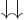 are often better replaced by the
triplet and singlet states
are often better replaced by the
triplet and singlet states 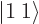 ,
, 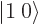 ,
,
![${\left\vert 1\:\rule[2.5pt]{5pt}{.5pt}1\right\rangle}$](img1079.gif) , and
, and 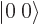 .
.

- The triplet and singlet states have definite values for the
net square spin.
5.5.6 Review Questions
-
1.
-
Like the states 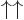 ,
, 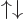 ,
, 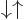 , and
, and 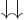 ; the triplet and singlet states are an orthonormal quartet. For example, check that the inner product of
; the triplet and singlet states are an orthonormal quartet. For example, check that the inner product of 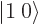 and
and 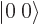 is zero.
is zero.
Solution complexse-a
![]() ,
,![]()
![]() -
-![]() ,
,![]()
![]() .
.![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
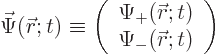
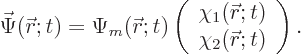
![]() ;
;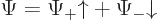

![]()
![]()
![]() ?
?![]()
![]()
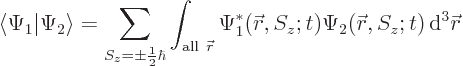
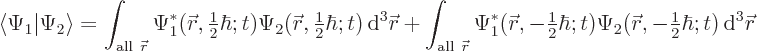
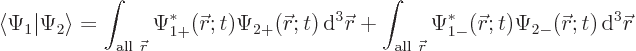
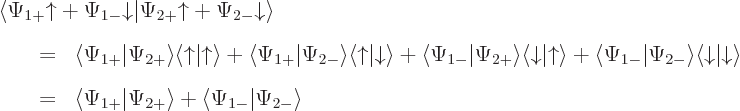
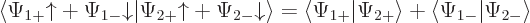
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() -
-![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() -
-![]() ?
?![]()
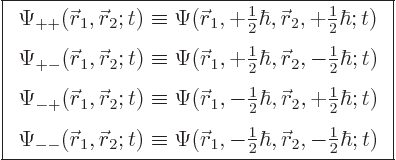
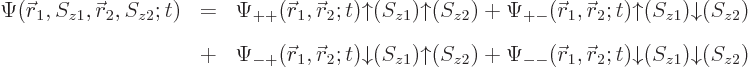
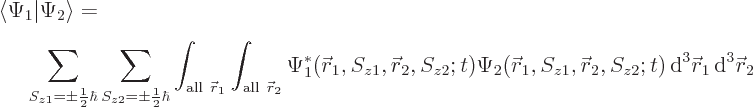
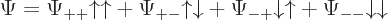
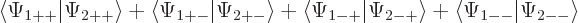
,
,
,
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![\begin{displaymath}
\sum_{{\rm all} S_{z1}} \sum_{{\rm all} S_{z2}} f(S_{z1}) ...
...S_{z1})\right] \left[\sum_{{\rm all} S_{z2}} g(S_{z2})\right]
\end{displaymath}](img1058.gif)
![\begin{eqnarray*}\lefteqn{\int_{{\rm all} {\skew0\vec r}_1} \int_{{\rm all} {\...
...ec r}_2} g({\skew0\vec r}_2) { \rm d}^3 {\skew0\vec r}_2\right]
\end{eqnarray*}](img1059.gif)
.
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
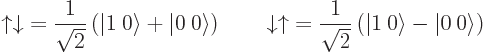
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
,
,
,
,
,
,
.
![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]()
![]()