|
|
|
|
|
Next: 5.7 Ways to Symmetrize the Wave Function |
|
A number of the counter-intuitive features of quantum mechanics have already been discussed: Electrons being neither on Mars or on Venus until they pop up at either place. Superluminal interactions. The fundamental impossibility of improving the accuracy of both position and momentum beyond a given limit. Collapse of the wave function. A hidden random number generator. Quantized energies and angular momenta. Nonexisting angular momentum vectors. Intrinsic angular momentum. But nature has one more trick on its sleeve, and it is a big one.
Nature entangles all identical particles with each other.
Specifically, it requires that the wave function remains unchanged if any two identical bosons are exchanged. If particles
![]()
![]()
| (5.27) |
On the other hand, nature requires that the wave function changes sign if any two identical fermions are exchanged. If
particles ![]()
![]()
| (5.28) |
In other words, the wave function must be symmetric with respect to exchange of identical bosons, and antisymmetric with respect to exchange of identical fermions. This greatly restricts what wave functions can be.
For example, consider what this means for the electron structure of
the hydrogen molecule. The approximate ground state of lowest energy
was in the previous section found to be
But since the two electrons are identical fermions, this wave function
must turn into its negative under exchange of the two electrons.
Exchanging the two electrons produces
Since each of the four spin states is independent from the others, the
coefficient of each of these states will have to be the negative of
the one of the nonexchanged version. For example, the coefficient
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,
So, due to the antisymmetrization requirement, the full wave function
of the ground state must be,
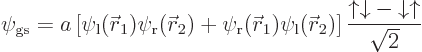
singletone, as defined in the previous section. It is the singlet spin state that achieves the sign change when the two electrons are exchanged; the spatial part remains the same.
If the electrons would have been bosons, the spin state could have been any combination of the three triplet states. The symmetrization requirement for fermions is much more restrictive than the one for bosons.
Since there are a lot more electrons in the universe than just these two, you might rightly ask where antisymmetrization stops. The answer given in chapter 8.3 is: nowhere. But don’t worry about it. The existence of electrons that are too far away to affect the system being studied can be ignored.
Key Points
- The wave function must be symmetric (must stay the same) under exchange of identical bosons.
- The wave function must be antisymmetric (must turn into its negative) under exchange of identical fermions (e.g., electrons.)
- Especially the antisymmetrization requirement greatly restricts what wave functions can be.
- The antisymmetrization requirement forces the electrons in the hydrogen molecule ground state to assume the singlet spin state.
Check that indeed any linear combination of the triplet states is unchanged under particle exchange.
Suppose the electrons of the hydrogen molecule are in the excited antisymmetric spatial state
Yes, in this case the spin would be less restricted if the electrons were bosons. But antisymmetric spatial states themselves are pretty restrictive in general. The precise sense in which the antisymmetrization requirement is more restrictive than the symmetrization requirement will be explored in the next section.