| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
5.7 Ways to Symmetrize the Wave Function
This section discusses ways in which the symmetrization requirements for
wave functions of systems of identical particles can be achieved in
general. This is a key issue in the numerical solution of any
nontrivial quantum system, so this section will examine it in some
detail.
It will be assumed that the approximate description of the wave
function is done using a set of chosen single-particle functions, or
states
,
An example is provided by the approximate ground state of the hydrogen
molecule from the previous section,
This can be multiplied out to be
and consists of four single-particle functions:
The first of the four functions represents a single electron in the
ground state around the left proton with spin up, the second a single
electron in the same spatial state with spin down, etcetera. For
better accuracy, more single-particle functions could be included, say
excited atomic states in addition to the ground states. In terms of
the above four functions, the expression for the hydrogen molecule
ground state is
The issue in this section is that the above hydrogen ground state is
just one special case of the most general wave function for the two
particles that can be formed from four single-particle states:
This can be written much more concisely using summation indices as
However, the individual terms will be fully written out for now to
reduce the mathematical abstraction. The individual terms are
sometimes called “Hartree products.”
The antisymmetrization requirement says that the wave function
must be antisymmetric under exchange of the two electrons. More
concretely, it must turn into its negative when the arguments
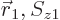 and
and 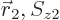 are swapped. To understand what
that means, the various terms need to be arranged in groups:
are swapped. To understand what
that means, the various terms need to be arranged in groups:
Within each group, all terms involve the same combination of
functions, but in a different order. Different groups have a
different combination of functions.
Now if the electrons are exchanged, it turns the terms in groups I
through IV back into themselves. Since the wave function must change
sign in the exchange, and something can only be its own negative if it
is zero, the antisymmetrization requirement requires that the
coefficients 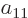 ,
, 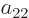 ,
,  , and
, and
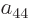 must all be zero. Four coefficients have been eliminated
from the list of unknown quantities.
must all be zero. Four coefficients have been eliminated
from the list of unknown quantities.
Further, in each of the groups V through X with two different states,
exchange of the two electrons turn the terms into each other, except
for their coefficients. If that is to achieve a change of sign, the
coefficients must be each other’s negatives; 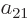

 ,
, 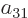

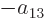 , ...
So only six coefficients
, ...
So only six coefficients 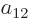 ,
, 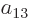 , ...still
need to be found from other physical requirements, such as energy
minimization for a ground state. Less than half of the original
sixteen unknowns survive the antisymmetrization requirement,
significantly reducing the problem size.
, ...still
need to be found from other physical requirements, such as energy
minimization for a ground state. Less than half of the original
sixteen unknowns survive the antisymmetrization requirement,
significantly reducing the problem size.
There is a very neat way of writing the antisymmetrized wave function
of systems of fermions, which is especially convenient for larger
numbers of particles. It is done using determinants. The
antisymmetric wave function for the above example is:

These determinants are called “Slater determinants”.
To find the actual hydrogen molecule ground state from the above
expression, additional physical requirements have to be imposed. For
example, the coefficients 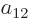 and
and 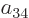 can reasonably be
ignored for the ground state, because according to the given
definition of the states, their Slater determinants have the electrons
around the same nucleus, and that produces elevated energy due to the
mutual repulsion of the electrons. Also, following the arguments of
section 5.2, the coefficients
can reasonably be
ignored for the ground state, because according to the given
definition of the states, their Slater determinants have the electrons
around the same nucleus, and that produces elevated energy due to the
mutual repulsion of the electrons. Also, following the arguments of
section 5.2, the coefficients 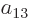 and
and 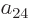 must be
zero since their Slater determinants produce the excited antisymmetric
spatial state
must be
zero since their Slater determinants produce the excited antisymmetric
spatial state 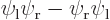 times the
times the 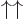 , respectively
, respectively 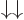 spin states. Finally,
the coefficients
spin states. Finally,
the coefficients 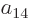 and
and 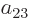 must be opposite in order that
their Slater determinants combine into the lowest-energy symmetric
spatial state
must be opposite in order that
their Slater determinants combine into the lowest-energy symmetric
spatial state 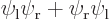 times the
times the 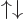 and
and 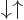 spin states. That leaves the single
coefficient
spin states. That leaves the single
coefficient 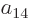 that can be found from the normalization
requirement, taking it real and positive for convenience.
that can be found from the normalization
requirement, taking it real and positive for convenience.
But the issue in this section is what the symmetrization requirements
say about wave functions in general, whether they are some ground
state or not. And for four single-particle states for two identical
fermions, the conclusion is that the wave function must be some
combination of the six Slater determinants, regardless of what other
physics may be relevant.
The next question is how that conclusion changes if the two particles
involved are not fermions, but identical bosons. The symmetrization
requirement is then that exchanging the particles must leave the wave
function unchanged. Since the terms in groups I through IV do remain
the same under particle exchange, their coefficients 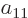 through
through
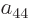 can have any nonzero value. This is the sense in which the
antisymmetrization requirement for fermions is much more restrictive
than the one for bosons: groups involving a duplicated state must be
zero for fermions, but not for bosons.
can have any nonzero value. This is the sense in which the
antisymmetrization requirement for fermions is much more restrictive
than the one for bosons: groups involving a duplicated state must be
zero for fermions, but not for bosons.
In groups V through X, where particle exchange turns each of the two
terms into the other one, the coefficients must now be equal instead
of negatives; 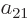

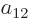 ,
, 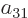

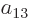 , ... That eliminates six coefficients
from the original sixteen unknowns, leaving ten coefficients that must
be determined by other physical requirements on the wave function.
, ... That eliminates six coefficients
from the original sixteen unknowns, leaving ten coefficients that must
be determined by other physical requirements on the wave function.
(The equivalent of Slater determinants for bosons are “permanents,” basically determinants with all minus signs in
their definition replaced by plus signs. Unfortunately, many of the
helpful properties of determinants do not apply to permanents.)
All of the above arguments can be extended to the general case that
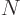 , instead of 4, single-particle functions
, instead of 4, single-particle functions
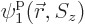 ,
, 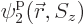 , ...,
, ..., 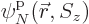 are used to describe
are used to describe  , instead of 2, particles. Then the
most general possible wave function assumes the form:
, instead of 2, particles. Then the
most general possible wave function assumes the form:
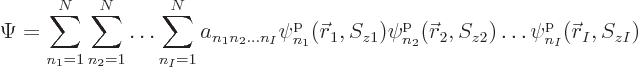 |
(5.30) |
where the 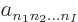 are numerical coefficients that are
to be chosen to satisfy the physical constraints on the wave function,
including the (anti) symmetrization requirements.
are numerical coefficients that are
to be chosen to satisfy the physical constraints on the wave function,
including the (anti) symmetrization requirements.
This summation is again the every possible combination
idea of combining every possible state for particle 1 with every
possible state for particle 2, etcetera. So the total sum above
contains 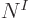 terms: there are
terms: there are 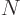 possibilities for the function
number
possibilities for the function
number 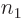 of particle 1, times
of particle 1, times 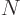 possibilities for the function
number
possibilities for the function
number 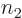 of particle 2, ... In general then, a corresponding
total of
of particle 2, ... In general then, a corresponding
total of 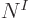 unknown coefficients
unknown coefficients 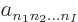 must be
determined to find out the precise wave function.
must be
determined to find out the precise wave function.
But for identical particles, the number that must be determined is
much less. That number can again be determined by dividing the terms
into groups in which the terms all involve the same combination of  single-particle functions, just in a different order. The simplest
groups are those that involve just a single single-particle function,
generalizing the groups I through IV in the earlier example. Such
groups consist of only a single term; for example, the group that only
involves
single-particle functions, just in a different order. The simplest
groups are those that involve just a single single-particle function,
generalizing the groups I through IV in the earlier example. Such
groups consist of only a single term; for example, the group that only
involves 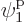 consists of the single term
consists of the single term
At the other extreme, groups in which every single-particle function is
different have as many as 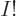 terms, since
terms, since 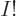 is the number of ways
that
is the number of ways
that  different items can be ordered. In the earlier example, that
were groups V through X, each having 2! = 2 terms. If there are more
than two particles, there will also be groups in which some states are
the same and some are different.
different items can be ordered. In the earlier example, that
were groups V through X, each having 2! = 2 terms. If there are more
than two particles, there will also be groups in which some states are
the same and some are different.
For identical bosons, the symmetrization requirement says that all the
coefficients within a group must be equal. Any term in a group can be
turned into any other by particle exchanges; so, if they would not all
have the same coefficients, the wave function could be changed by
particle exchanges. As a result, for identical bosons the number of
unknown coefficients reduces to the number of groups.
For identical fermions, only groups in which all single-particle
functions are different can be nonzero. That follows because if a
term has a duplicated single-particle function, it turns into itself
without the required sign change under an exchange of the particles of
the duplicated function.
So there is no way to describe a system of  identical fermions with
anything less than
identical fermions with
anything less than  different single-particle functions
different single-particle functions
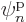 . This critically important observation is known as
the “Pauli exclusion principle:”
. This critically important observation is known as
the “Pauli exclusion principle:” 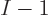 fermions occupying
fermions occupying 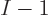 single-particle functions exclude a
single-particle functions exclude a  -th fermion from simply
entering the same
-th fermion from simply
entering the same 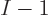 functions; a new function must be added to the
mix for each additional fermion. The more identical fermions there
are in a system, the more different single-particle functions are
required to describe it.
functions; a new function must be added to the
mix for each additional fermion. The more identical fermions there
are in a system, the more different single-particle functions are
required to describe it.
Each group involving  different single-particle functions
different single-particle functions
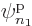 ,
, 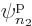 , ...
, ...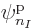 reduces
under the antisymmetrization requirement to a single Slater
determinant of the form
reduces
under the antisymmetrization requirement to a single Slater
determinant of the form
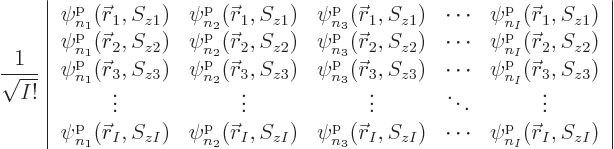 |
(5.31) |
multiplied by a single unknown coefficient. The normalization factor
1
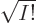 has been thrown in merely to ensure that if the
functions
has been thrown in merely to ensure that if the
functions 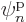 are orthonormal, then so are the Slater
determinants. Using Slater determinants ensures the required sign
changes of fermion systems automatically, because determinants change
sign if two rows are exchanged.
are orthonormal, then so are the Slater
determinants. Using Slater determinants ensures the required sign
changes of fermion systems automatically, because determinants change
sign if two rows are exchanged.
In the case that the bare minimum of  functions is used to describe
functions is used to describe
 identical fermions, only one Slater determinant can be formed.
Then the antisymmetrization requirement reduces the
identical fermions, only one Slater determinant can be formed.
Then the antisymmetrization requirement reduces the 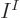 unknown
coefficients
unknown
coefficients 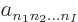 to just one,
to just one,
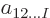 ; obviously a tremendous reduction.
; obviously a tremendous reduction.
At the other extreme, when the number of functions 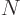 is very large,
much larger than
is very large,
much larger than 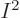 to be precise, most terms have all indices
different and the reduction is
to be precise, most terms have all indices
different and the reduction is only
from 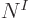 to
about
to
about 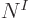

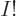 terms. The latter would also be true for identical
bosons.
terms. The latter would also be true for identical
bosons.
The functions better be chosen to produce a good approximation to the
wave function with a small number of terms. As an arbitrary example
to focus the thoughts, if 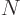
 100 functions are used to describe
an arsenic atom, with
100 functions are used to describe
an arsenic atom, with 
 33 electrons, there would be a
prohibitive 10
33 electrons, there would be a
prohibitive 10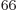 terms in the sum (5.30). Even after
reduction to Slater determinants, there would still be a prohibitive
3 10
terms in the sum (5.30). Even after
reduction to Slater determinants, there would still be a prohibitive
3 10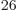 or so unknown coefficients left. The precise expression for
the number of Slater determinants is called “
or so unknown coefficients left. The precise expression for
the number of Slater determinants is called “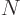 choose
choose
 ;” it is given by
;” it is given by
since the top gives the total number of terms that have all functions
different, (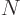 possible functions for particle 1, times
possible functions for particle 1, times  possible functions left for particle 2, etcetera,) and the bottom
reflects that it takes
possible functions left for particle 2, etcetera,) and the bottom
reflects that it takes 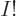 of them to form a single Slater
determinant. {D.25}.
of them to form a single Slater
determinant. {D.25}.
The basic Hartree-Fock
approach, discussed in chapter
9.3, goes to the extreme in reducing the number of functions:
it uses the very minimum of  single-particle functions. However,
rather than choosing these functions a priori, they are adjusted to
give the best approximation that is possible with a single Slater
determinant. Unfortunately, if a single determinant still turns out
to be not accurate enough, adding a few more functions quickly blows
up in your face. Adding just one more function gives
single-particle functions. However,
rather than choosing these functions a priori, they are adjusted to
give the best approximation that is possible with a single Slater
determinant. Unfortunately, if a single determinant still turns out
to be not accurate enough, adding a few more functions quickly blows
up in your face. Adding just one more function gives  more
determinants; adding another function gives another
more
determinants; adding another function gives another 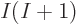
 2 more
determinants, etcetera.
2 more
determinants, etcetera.
Key Points

- Wave functions for multiple-particle systems can be formed using
sums of products of single-particle wave functions.

- The coefficients of these products are constrained by the
symmetrization requirements.

- In particular, for identical fermions such as electrons, the
single-particle wave functions must combine into Slater
determinants.

- Systems of identical fermions require at least as many
single-particle states as there are particles. This is known as the
Pauli exclusion principle.

- If more single-particle states are used to describe a system,
the problem size increases rapidly.
5.7 Review Questions
-
1.
-
How many single-particle states would a basic Hartree-Fock approximation use to compute the electron structure of an arsenic atom? How many Slater determinants would that involve?
Solution symways-a
-
2.
-
If two more single-particle states would be used to improve the accuracy for the arsenic atom, (one more normally does not help), how many Slater determinants could be formed with those states?
Solution symways-b

![\begin{eqnarray*}
&&
\frac{a}{\sqrt2}
\Big[
\psi_{\rm {l}}({\skew0\vec r}_1)...
...S_{z1})\psi_{\rm {l}}({\skew0\vec r}_2){\uparrow}(S_{z2})
\Big]
\end{eqnarray*}](img1094.gif)
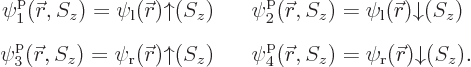
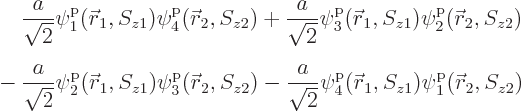
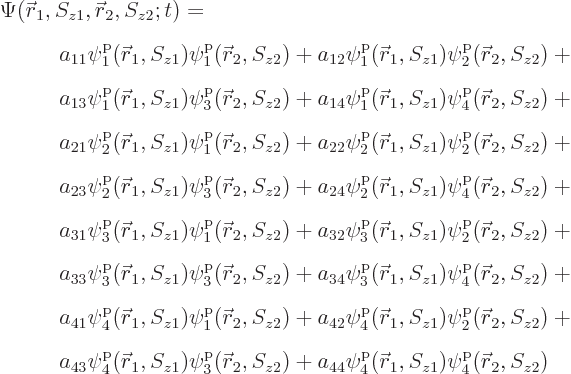
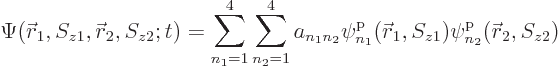
![]()
![]()

![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() -
-![]()
![]()
![]() ,
,![]() ,
,![]()
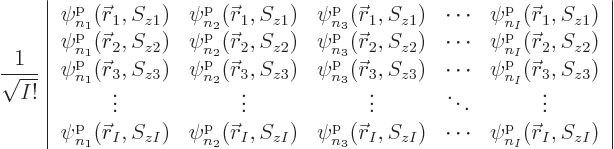
![]()
![]()
![]()
![]()
![]() ;
;![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;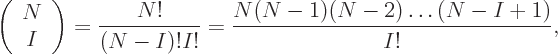
![]()
![]()
![]()
![]()