| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12. Angular momentum
The quantum mechanics of angular momentum is fascinating. It is also
very basic to much of quantum mechanics. It is a model for dealing
with other systems of particles
In chapter 5.4, it was already mentioned that angular
momentum of particles comes in two basic kinds. Orbital angular
momentum is a result of the angular motion of particles, while spin is
built-in
angular momentum of the particles.
Orbital angular momentum is usually indicated by 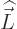 and spin
angular momentum by
and spin
angular momentum by 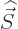 . A system of particles will normally
involve both orbital and spin angular momentum. The combined angular
momentum is typically indicated by
. A system of particles will normally
involve both orbital and spin angular momentum. The combined angular
momentum is typically indicated by
However, this chapter will use 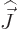 as a generic name for any angular
momentum. So in this chapter
as a generic name for any angular
momentum. So in this chapter 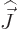 can indicate orbital angular
momentum, spin angular momentum, or any combination of the two.
can indicate orbital angular
momentum, spin angular momentum, or any combination of the two.
Subsections
![]()
![]() .
.![]()
![]()