| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.7 Clebsch-Gordan coefficients
In classical physics, combining angular momentum from different
sources is easy; the net components in the  ,
, 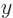 , and
, and
 directions are simply the sum of the individual components. In
quantum mechanics, things are trickier, because if the component in
the
directions are simply the sum of the individual components. In
quantum mechanics, things are trickier, because if the component in
the  -direction exists, those in the
-direction exists, those in the  and
and 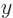 directions do not.
But the previous subsection showed how to the spin angular momenta of
two spin
directions do not.
But the previous subsection showed how to the spin angular momenta of
two spin 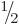 particles could be combined. In similar ways, the
angular momentum states of any two ladders, whatever their origin, can
be combined into net angular momentum ladders. And then those ladders
can in turn be combined with still other ladders, allowing net angular
momentum states to be found for systems of arbitrary complexity.
particles could be combined. In similar ways, the
angular momentum states of any two ladders, whatever their origin, can
be combined into net angular momentum ladders. And then those ladders
can in turn be combined with still other ladders, allowing net angular
momentum states to be found for systems of arbitrary complexity.
The key is to be able to combine the angular momentum ladders from two
different sources into net angular momentum ladders. To do so, the
net angular momentum can in principle be described in terms of product
states in which each source is on a single rung of its ladder. But as
the example of the last section illustrated, such product states give
incomplete information about the net angular momentum; they do not
tell you what square net angular momentum is. You need to know
what combinations of product states produce rungs on the ladders of
the net angular momentum, like the ones illustrated in figure
12.3. In particular, you need to know the coefficients that
multiply the product states in those combinations.
Figure 12.4:
Clebsch-Gordan coefficients of two spin one half particles.
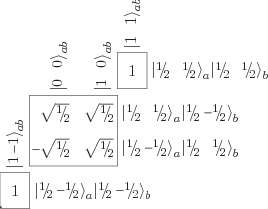 |
These coefficients are called Clebsch-Gordan
coefficients. The ones corresponding to figure 12.3 are
tabulated in Figure 12.4. Note that there are really three
tables of numbers; one for each rung level. The top, single number,
table
says that the 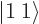 net momentum state is
found in terms of product states as:
net momentum state is
found in terms of product states as:
The second table gives the states with zero net angular momentum in
the  -direction. For example, the first column of the table says
that the
-direction. For example, the first column of the table says
that the 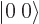 singlet state is found as:
singlet state is found as:
Similarly the second column gives the middle rung 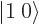 on the triplet
ladder. The bottom
on the triplet
ladder. The bottom table
gives the bottom rung of
the triplet ladder.
You can also read the tables horizontally {N.29}. For
example, the first row of the middle table says that the
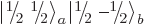 product state equals
product state equals
That in turn implies that if the net square angular momentum of
this product state is measured, there is a 50/50 chance of it turning
out to be either zero, or the 
 1 (i.e.
1 (i.e. 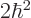 ) value. The
) value. The
 -momentum will always be zero.
-momentum will always be zero.
Figure 12.5:
Clebsch-Gordan coefficients when the second angular
momentum contribution has azimuthal quantum number 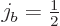 .
.
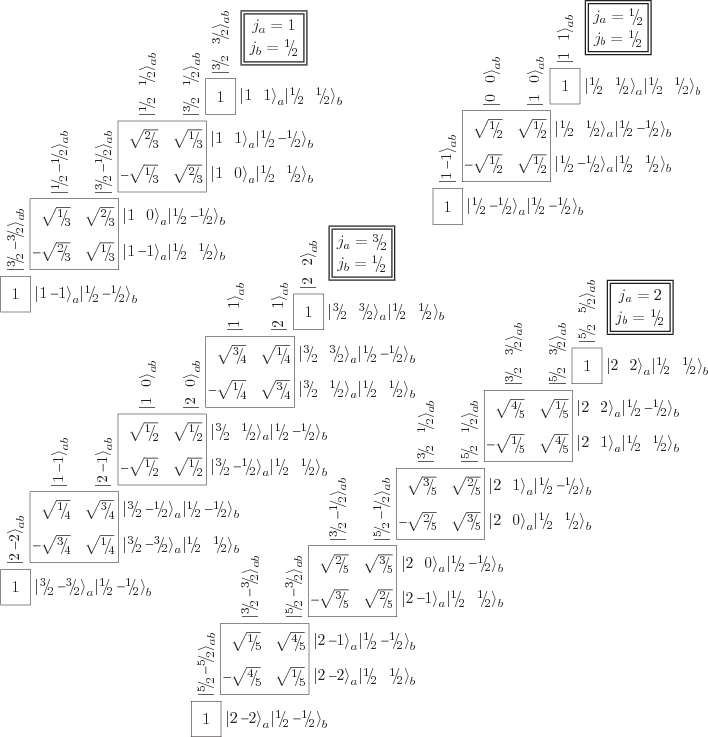 |
Figure 12.6:
Clebsch-Gordan coefficients when the second angular momentum
contribution has azimuthal quantum number 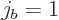 .
.
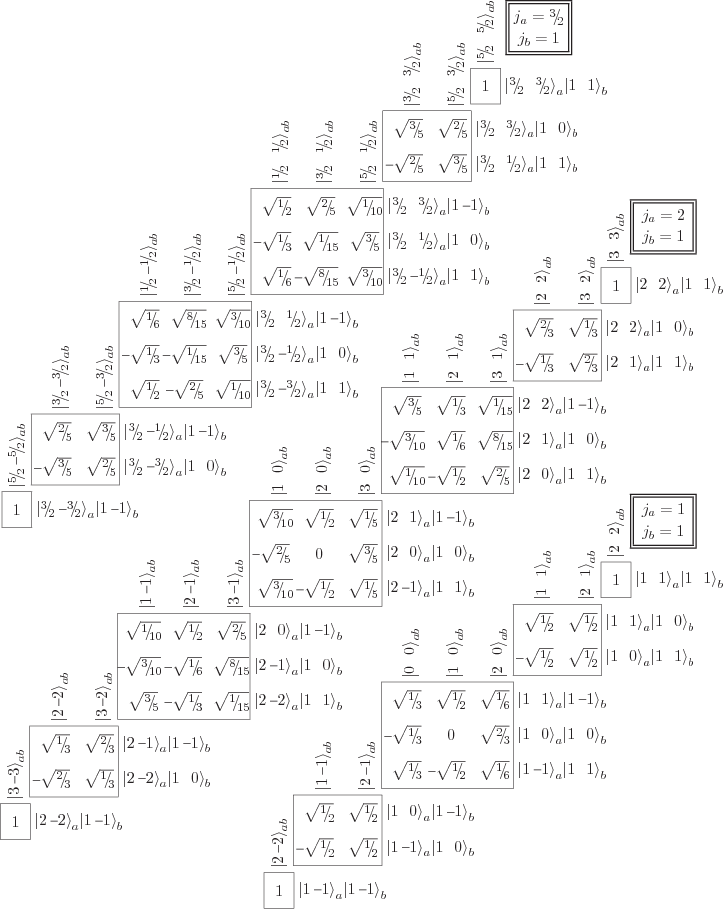 |
How about the Clebsch-Gordan coefficients to combine other ladders
than the spins of two spin 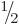 particles? Well, the same
procedures used in the previous section work just as well to combine
the angular momenta of any two angular momentum ladders, whatever
their size. Just the thing for a long winter night. Or, if you live
in Florida, you just might want to write a little computer program
that does it for you {D.65} and outputs the tables in
human-readable form {N.30}, like figures 12.5 and
12.6.
particles? Well, the same
procedures used in the previous section work just as well to combine
the angular momenta of any two angular momentum ladders, whatever
their size. Just the thing for a long winter night. Or, if you live
in Florida, you just might want to write a little computer program
that does it for you {D.65} and outputs the tables in
human-readable form {N.30}, like figures 12.5 and
12.6.
From the figures you may note that when two states with total angular
momentum quantum numbers 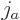 and
and 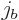 are combined, the
combinations have total angular quantum numbers ranging from
are combined, the
combinations have total angular quantum numbers ranging from 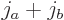 to
to 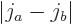 . This is similar to the fact that when in
classical mechanics two angular momentum vectors are combined, the
combined total angular momentum
. This is similar to the fact that when in
classical mechanics two angular momentum vectors are combined, the
combined total angular momentum 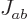 is at most
is at most 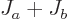 and at
least
and at
least 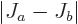 . (The so-called “triangle
inequality” for combining vectors.) But of course,
. (The so-called “triangle
inequality” for combining vectors.) But of course,  is not
quite a proportional measure of
is not
quite a proportional measure of 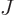 unless
unless 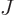 is large; in fact,
is large; in fact, 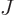

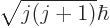 {D.66}.
{D.66}.
![]() ,
,![]() ,
,![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
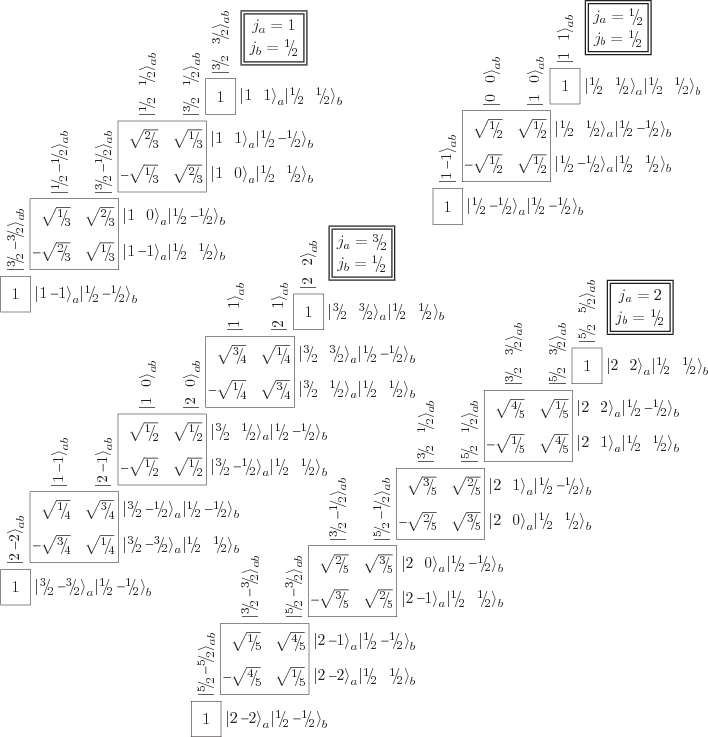
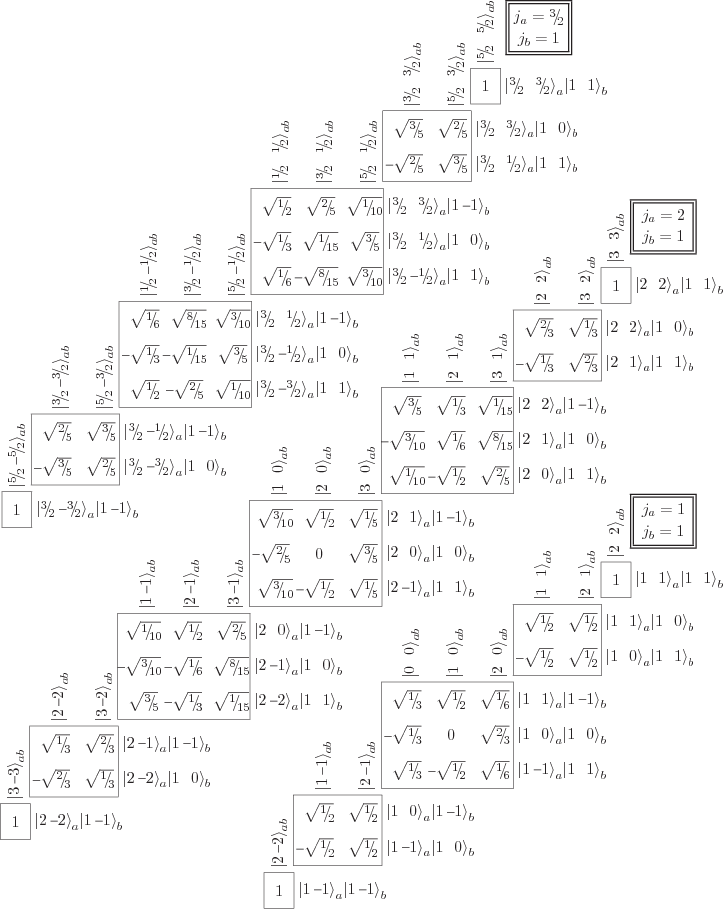
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()