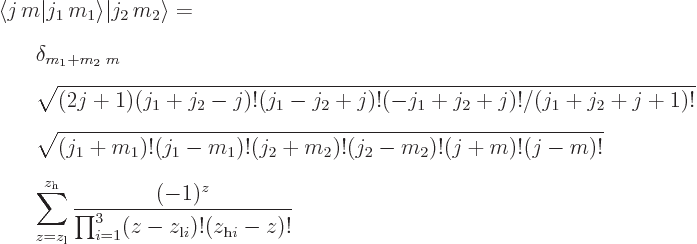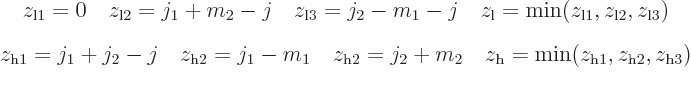| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.65 How to make Clebsch-Gordan tables
The procedure of finding the Clebsch-Gordan coefficients for the
combination of any two spin ladders is exactly the same as for
electron ones, so it is simple enough to program.
To further simplify things, it turns out that the coefficients are all
square roots of rational numbers (i.e. ratios of integers such as
102/38.) The step-up and step-down operators by themselves produce
square roots of rational numbers, so at first glance it would appear
that the individual Clebsch-Gordan coefficients would be sums of
square roots. But the square roots of a given coefficient are all
compatible and can be summed into one. To see why, consider the
coefficients that result from applying the combined step down ladder
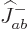 a few times on the top of the ladder
a few times on the top of the ladder
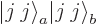 . Every contribution to the coefficient
of a state
. Every contribution to the coefficient
of a state 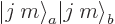 comes from applying
comes from applying 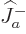 for
for
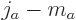 times and
times and 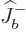 for
for 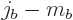 times, so all contributions
have compatible square roots.
times, so all contributions
have compatible square roots. 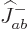 merely adds an
merely adds an 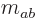 dependent normalization factor.
dependent normalization factor.
You might think this pattern would be broken when you start defining
the tops of lower ladders, since that process uses the step up
operators. But because 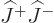 and
and 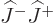 are rational numbers
(not square roots), applying the up operators is within a rational
number the same as applying the down ones, and the pattern turns out
to remain.
are rational numbers
(not square roots), applying the up operators is within a rational
number the same as applying the down ones, and the pattern turns out
to remain.
Additional note: There is also a direct expression for the
Clebsch-Gordan coefficients:
where 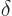 is the Kronecker delta and
is the Kronecker delta and
Carefully coded, this one seems to be numerically superior at larger
angular momenta. Either way, these coefficients will overflow pretty
quickly.
There are also resources on the web to compute these coefficients.
See {N.13} for additional information.
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()