| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.11 General spin matrices
The arguments that produced the Pauli spin matrices for a system with
spin 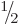 work equally well for systems with larger square
angular momentum.
work equally well for systems with larger square
angular momentum.
In particular, from the definition of the ladder operators
it follows by taking the sum, respectively difference, that
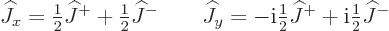 |
(12.17) |
Therefore, the effect of either 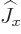 or
or 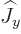 is to produce
multiples of the states with the next higher and the next lower
magnetic quantum number. The multiples can be determined using
(12.9) and (12.10).
is to produce
multiples of the states with the next higher and the next lower
magnetic quantum number. The multiples can be determined using
(12.9) and (12.10).
If you put these multiples again in matrices, after ordering the
states by magnetic quantum number, you get Hermitian tridiagonal
matrices with nonzero sub and superdiagonals and zero main diagonal,
where 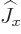 is real symmetric while
is real symmetric while 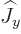 is purely imaginary, equal
to
is purely imaginary, equal
to 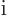 times a real skew-symmetric matrix. Be sure to tell all you
friends that you heard it here first. Do watch out for the
well-informed friend who may be aware that forming such matrices is
bad news anyway since they are almost all zeros. If you want to use
canned matrix software, at least use the kind for tridiagonal
matrices.
times a real skew-symmetric matrix. Be sure to tell all you
friends that you heard it here first. Do watch out for the
well-informed friend who may be aware that forming such matrices is
bad news anyway since they are almost all zeros. If you want to use
canned matrix software, at least use the kind for tridiagonal
matrices.
![]()
![]()
![]()
![]()
![]()
![]()