| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.10 Pauli spin matrices
This subsection returns to the simple two-rung spin ladder (doublet)
of an electron, or any other spin 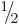 particle for that
matter, and tries to tease out some more information about the spin.
While the analysis so far has made statements about the angular
momentum in the arbitrarily chosen
particle for that
matter, and tries to tease out some more information about the spin.
While the analysis so far has made statements about the angular
momentum in the arbitrarily chosen  -direction, you often also need
information about the spin in the corresponding
-direction, you often also need
information about the spin in the corresponding  and
and  directions. This subsection will find it.
directions. This subsection will find it.
But before getting at it, a matter of notations. It is customary to
indicate angular momentum that is due to spin by a capital 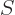 .
Similarly, the azimuthal quantum number of spin is indicated by
.
Similarly, the azimuthal quantum number of spin is indicated by
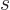 . This subsection will follow this convention.
. This subsection will follow this convention.
Now, suppose you know that the particle is in the
spin-up
state with 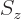

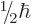 angular
momentum in a chosen
angular
momentum in a chosen  direction; in other words that it is in the
direction; in other words that it is in the
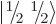 , or
, or 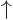 , state. You want the effect of the
, state. You want the effect of the
 and
and 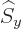 operators on this state. In the absence of a
physical model for the motion that gives rise to the spin, this may
seem like a hard question indeed. But again the faithful ladder
operators
operators on this state. In the absence of a
physical model for the motion that gives rise to the spin, this may
seem like a hard question indeed. But again the faithful ladder
operators  and
and 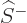 clamber up and down to your rescue!
clamber up and down to your rescue!
Assuming that the normalization factor of the 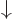 state is
chosen in terms of the one of the
state is
chosen in terms of the one of the 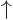 state consistent with the
ladder relations (12.9) and (12.10), you have:
state consistent with the
ladder relations (12.9) and (12.10), you have:
By adding or subtracting the two equations, you find the effects of
 and
and 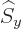 on the spin-up state:
on the spin-up state:
It works the same way for the spin-down state 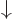

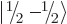 :
:
You now know the effect of the  and
and  angular momentum operators
on the
angular momentum operators
on the  -direction spin states. Chalk one up for the ladder
operators.
-direction spin states. Chalk one up for the ladder
operators.
Next, assume that you have some spin state that is an arbitrary
combination of spin-up and spin-down:
Then, according to the expressions above, application of the
 spin operator
spin operator  will turn it into:
will turn it into:
while the operator 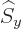 turns it into
turns it into
And of course, since 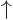 and
and 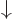 are the eigenstates of
are the eigenstates of
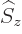 ,
,
If you put the coefficients in the formula above, except for the
common factor 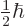 , in little 2
, in little 2 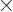 2 tables,
you get the so-called
2 tables,
you get the so-called Pauli spin matrices
:
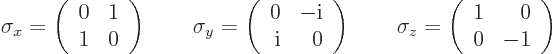 |
(12.15) |
where the convention is that 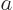 multiplies the first column of the
matrices and
multiplies the first column of the
matrices and 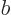 the second. Also, the top rows in the matrices
produce the spin-up part of the result and the bottom rows the spin
down part. In linear algebra, you also put the coefficients
the second. Also, the top rows in the matrices
produce the spin-up part of the result and the bottom rows the spin
down part. In linear algebra, you also put the coefficients 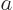 and
and 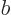 together in a vector:
together in a vector:
You can now go further and find the eigenstates of the  and
and 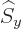 operators in terms of the
eigenstates
operators in terms of the
eigenstates 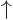 and
and 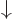 of the
of the 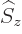 operator. You
can use the techniques of linear algebra, or you can guess. For
example, if you guess
operator. You
can use the techniques of linear algebra, or you can guess. For
example, if you guess 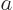

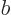
 1,
1,
so 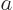

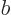
 1 is an eigenstate of
1 is an eigenstate of  with eigenvalue
with eigenvalue
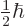 , call it a
, call it a  ,
,
spin-right
, state. To normalize the state, you still
need to divide by 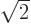 :
:
Similarly, you can guess the other eigenstates, and come up with:
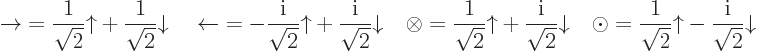 |
(12.16) |
Note that the square magnitudes of the coefficients of the states are
all one half, giving a 50/50 chance of finding the  -momentum up or
down. Since the choice of the axis system is arbitrary, this can be
generalized to mean that if the spin in a given direction has an
definite value, then there will be a 50/50 chance of the spin in any
orthogonal direction turning out to be
-momentum up or
down. Since the choice of the axis system is arbitrary, this can be
generalized to mean that if the spin in a given direction has an
definite value, then there will be a 50/50 chance of the spin in any
orthogonal direction turning out to be 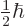 or
or
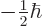 .
.
You might wonder about the choice of normalization factors in the spin
states (12.16). For example, why not leave out the common
factor 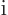 in the
in the 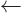 , (negative
, (negative  spin, or
spin-left), state? The reason is to ensure that the
spin, or
spin-left), state? The reason is to ensure that the
 -direction ladder operator
-direction ladder operator 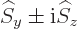 and the
and the
 -direction one
-direction one 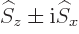 , as obtained by
cyclic permutation of the ones for
, as obtained by
cyclic permutation of the ones for  , produce real, positive
multiplication factors. This allows relations valid in the
, produce real, positive
multiplication factors. This allows relations valid in the
 -direction (like the expressions for triplet and singlet
states) to also apply in the
-direction (like the expressions for triplet and singlet
states) to also apply in the  and
and  directions. In addition,
with this choice, if you do a simple change in the labeling of the
axes, from
directions. In addition,
with this choice, if you do a simple change in the labeling of the
axes, from 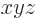 to
to 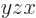 or
or 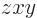 , the form of the Pauli spin
matrices remains unchanged. The
, the form of the Pauli spin
matrices remains unchanged. The  and
and  states of
positive
states of
positive  -, respectively
-, respectively  -momentum were chosen a
different way: if you rotate the axis system 90
-momentum were chosen a
different way: if you rotate the axis system 90 around
the
around
the  or
or  axis, these are the spin-up states along the new
axis, these are the spin-up states along the new
 -axis, the
-axis, the  -axis or
-axis or  -axis in the system you
are looking at now, {D.68}.
-axis in the system you
are looking at now, {D.68}.
![]()
![]() -
-![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
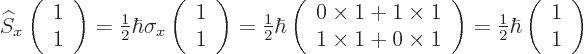
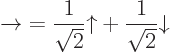
![]() -
-![]()
![]() .
.![]()
![]() ,
,![]()
![]() -
-![]()
![]() -
-![]() ,
,![]() ,
,![]() -
-![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() -
-![]() -
-![]()
![]()
![]()
![]() -
-![]() -
-![]() -
-