12.1 In­tro­duc­tion

The stan­dard eigen­func­tions of or­bital an­gu­lar mo­men­tum are the so called spher­i­cal har­mon­ics of chap­ter 4.2. They show that the square or­bital an­gu­lar mo­men­tum has the pos­si­ble val­ues

$$L^2 \equiv L_x^2+L_y^2+L_z^2 = l(l+1) \hbar^2 \quad \mbox{where $l$ is one of 0, 1, 2, 3, \ldots}$$

The non­neg­a­tive in­te­ger $l$ is called the az­imuthal quan­tum num­ber.

Fur­ther, the or­bital an­gu­lar mo­men­tum in any ar­bi­trar­ily cho­sen di­rec­tion, taken as the $z$-​di­rec­tion from now on, comes in mul­ti­ples $m$ of Planck's con­stant $\hbar$:

$$L_z = m_l\hbar \quad \mbox{where $m_l$ is one of $-l$, $-l{+}1$, $-l{+}2$, \ldots, $l{-}1$, $l$.}$$

The in­te­ger 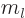$m_l$ is called the mag­netic quan­tum num­ber.

The pos­si­ble val­ues of the square spin an­gu­lar mo­men­tum can be writ­ten as

$$S^2 \equiv S_x^2+S_y^2+S_z^2 = s(s+1)\hbar^2 \quad \quad \... ...n-.21em\lower.56ex\hbox{\the\scriptfont0 2}\kern.05em, \ldots}$$

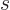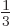The spin az­imuthal quan­tum num­ber $s$ is usu­ally called the spin for short. Note that while the or­bital az­imuthal quan­tum num­ber $l$ had to be an in­te­ger, the spin can be half in­te­ger. But one im­por­tant con­clu­sion of this chap­ter will be that the spin can­not be any­thing more. A par­ti­cle with, say, spin $\frac13$ can­not not ex­ist ac­cord­ing to the the­ory.

For the spin an­gu­lar mo­men­tum in the $z$-​di­rec­tion

$$S_z = m_s\hbar \quad \mbox{where $m_s$ is one of $-s$, $-s{+}1$, $-s{+}2$, \ldots, $s{-}1$, $s$.}$$

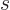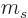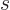Note that if the spin $s$ is half in­te­ger, then so are all the spin mag­netic quan­tum num­bers $m_s$. If the na­ture of the an­gu­lar mo­men­tum is self-ev­i­dent, the sub­script $l$ or $s$ of the mag­netic quan­tum num­bers $m$ will be omit­ted.

Par­ti­cles with half-in­te­ger spin are called fermi­ons. That in­cludes elec­trons, as well as pro­tons and neu­trons and their con­stituent quarks. All of these crit­i­cally im­por­tant par­ti­cles have spin 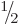$\leavevmode \kern.03em\raise.7ex\hbox{\the\scriptfont0 1}\kern-.2em /\kern-.21em\lower.56ex\hbox{\the\scriptfont0 2}\kern.05em$. (Ex­cited pro­ton and neu­tron states can have spin 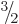$\leavevmode \kern.03em\raise.7ex\hbox{\the\scriptfont0 3}\kern-.2em /\kern-.21em\lower.56ex\hbox{\the\scriptfont0 2}\kern.05em$.) Par­ti­cles with in­te­ger spin are bosons. That in­cludes the par­ti­cles that act as car­ri­ers of fun­da­men­tal forces; the pho­tons, in­ter­me­di­ate vec­tor bosons, glu­ons, and gravi­tons. All of these have spin 1, ex­cept the gravi­ton which sup­pos­edly has spin 2.