|
|
|
|
|
Next: 12. Angular momentum |
|
The specific heat of a substance describes its absorption of heat in
terms of its temperature change. In particular, the specific heat at
constant volume, ![]() ,
,
As a first example, consider simple monatomic ideal gases, and in
particular noble gases. Basic physics, or section 11.14.4,
shows that for an ideal gas, the molecules have ![]()
![]()
![]()
![]()
![]()
![]() .
.![]() )
)![]()
![]()
![]()
| (11.63) |
molecular mass,without units. Just use the values and ignore the name and the missing units of kg/kmol. See the notations for more.)
Many important ideal gases, such as hydrogen, as well as the oxygen
and nitrogen that make up air, are diatomic. Now if we assume that
the two atoms are point-size masses somehow rigidly connected to each
other, we still have that the center of the entire molecule can move
in three different directions, accounting for ![]()
![]()
![]()
![]() .
.
But note that these experimental data show that there are problems,
both at very low temperatures, and at very high ones. And there are
major theoretical problems too. Surely the connection between the
atoms is not going to be infinitely rigid. Allowing for that, we now
have two individual atoms that can each move in three different
directions independently of each other. That raises the kinetic
energy to ![]() .
.![]()
![]() .
.
It was all a big problem for classical physics. Not to mention that, as Maxwell noted, if you really take classical theory at face value, things get far, far, worse still, since the individual internal parts of the atoms, like the individual electrons and quarks in the nuclei, would each have to absorb their own thermal energy too. This should produce enormously high specific heats.
 |
Hydrogen in particular was a mystery before the advent of quantum
mechanics: at low temperatures it would behave as a monatomic
gas, with a specific heat of ![]()
Quantum mechanics solved this problem. In quantum mechanics the
angular momentum of the molecule, and so the corresponding kinetic
energy, as well as the harmonic oscillation energy, are quantized.
For hydrogen at low temperatures, the typical available thermal energy
![]()
frozen out.
At normal temperatures, there is enough thermal energy to reach the
states where the molecule rotates normal to the line connecting the
atoms, and the specific heat becomes
| (11.64) |
For high enough temperature, the vibrational modes will start becoming
active, and the specific heats will start inching up towards 3.5
![]()
![]()
These differences may be understood qualitatively if the motion is
modeled as a simple harmonic oscillator as discussed in chapter
4.1. The energy levels of an harmonic oscillator are apart
by an amount ![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
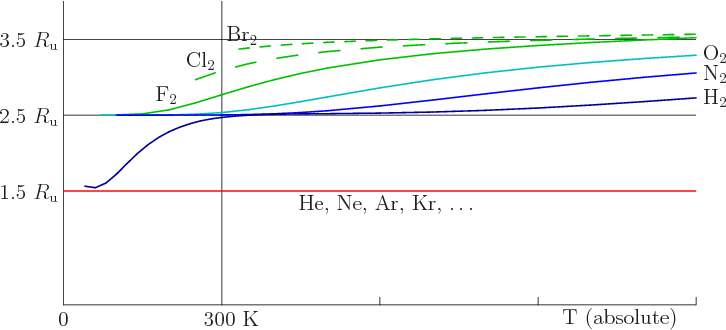
Following this reasoning, you would expect fluorine, which is held
together with only a single covalent bond, to have a higher specific
heat still, and figure 11.15 confirms it. And chlorine and
bromine, also held together by a single covalent bond, but heavier
than fluorine, approach the classical value 3.5 ![]()
![]()
![]()
![]()
![]() .
.
For solids, the basic classical idea in terms of atomic motion would
be that there would be ![]()
![]()
| (11.65) |
Note that typically for solids ![]() ,
,![]() .
.![]()
![]()
Dulong and Petit also works for liquid water if you take it per kmol
of atoms, rather than kmol of molecules, but not for ice. Ice has 4.6
![]()
![]()
![]()
![]() H
H![]() .
.![]()
Complex molecules may be an understandable problem for the law of
Dulong and Petit, but how come that diamond has about 0.73
![]() ,
,![]() ,
,![]()
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,19...
...0,0)[l]{Pb}}
\put(177,17){\makebox(0,0)[l]{H$_2$O}}
\end{picture}
\end{figure}](img2620.gif) |
Actually, it turns out, figure 11.16, that at much higher
temperatures diamond does agree nicely with the Dulong and
Petit value. Conversely, if the elements that agree well with Dulong
and Petit at room temperature are cooled to low temperatures, they too
have a specific heat that is much lower than the Dulong and Petit
value. For example, at 77 K, aluminum has 1.09 ![]() ,
,
It turns out that for all of them a characteristic temperature can by found above which the specific heat is about the Dulong and Petit value, but below which the specific heat starts dropping precariously. This characteristic temperature is called the Debye temperature. For example, aluminum, copper, gold, and iron have Debye temperatures of 394, 315, 170, and 460 K, all near or below room temperature, and their room temperature specific heats agree reasonably with the Dulong and Petit value. Conversely, diamond, boron, and beryllium have Debye temperatures of 1 860, 1 250, and 1 000 K, and their specific heats are much too low at room temperature.
The lack of heat capacity below the Debye temperature is again a
matter of frozen out
vibrational modes, like the
freezing out of the vibrational modes that gave common diatomic ideal
gases a heat capacity of only ![]()
![]() .
.
Atoms in a solid cannot be considered independent harmonic oscillators like the pairs of atoms in diatomic molecules. If an atom in a solid moves, its neighbors are affected. The proper way to describe the motion of the atoms is in terms of crystal-wide vibrations, such as those that in normal continuum mechanics describe acoustical waves. There are three variants of such waves, corresponding to the three independent directions the motion of the atoms can take with respect to the propagation direction of the wave. The atoms can move in the same direction, like in the acoustics of air in a pipe, or in a direction normal to it, like surface waves in water. Those are called longitudinal and transverse waves respectively. If there is more than one atom in the basis from which the solid crystal is formed, the atoms in a basis can also vibrate relative to each other’s position in high-frequency vibrations called optical modes. However, after such details are accounted for, the classical internal energy of a solid is still the Dulong and Petit value.
Enter quantum mechanics. Just like quantum mechanics says that the
energy of vibrating electromagnetic fields of frequency ![]()
![]() ,
,phonons
with energy ![]() .
.![]() ,
,![]()
![]()
![]()
Quantum mechanics did not just solve the low temperature problems for
heat capacity; it also solved the electron problem. That problem was
that classically electrons in at least metals too should have
![]()
![]() ,
,
Also, when the heat capacity due to the atom vibrations levels off to the Dulong and Petit value, that of the valence electrons keeps growing. Furthermore, at higher temperatures the increased vibrations lead to increased deviations in potential from the harmonic oscillator relationship. Wikipedia, Debye model, says anharmonicity causes the heat capacity to rise further; apparently authoritative other sources say that it can either increase or decrease the heat capacity. In any case, typical solids do show an increase of the heat capacity above the Dulong and Petit value at higher temperatures, figure 11.16.