| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
11. Basic and Quantum Thermodynamics
Chapter 6 mentioned the Maxwell-Boltzmann, Fermi-Dirac,
and Bose-Einstein energy distributions of systems of weakly
interacting particles. This chapter explains these results and then
goes on to put quantum mechanics and thermodynamics in context.
It is assumed that you have had a course in basic thermodynamics. If
not, rejoice, you are going to get one now. The exposition depends
relatively strongly upon the material in chapter
5.7-5.9 and chapter
6.1-6.16.
This chapter will be restricted to systems of particles that are all
the same. Such a system is called a “pure substance.” Water would be a pure substance, but air not
really; air is mostly nitrogen, but the 20% oxygen can probably not
be ignored. That would be particularly important under cryogenic
conditions in which the oxygen condenses out first.
The primary quantum system to be studied in detail will be a
macroscopic number of weakly interacting particles, especially
particles in a box. Nontrivial interactions between even a few
particles are very hard to account for correctly, and for a
macroscopic system, that becomes much more so: just a millimol has
well over 10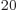 particles. By ignoring particle interactions, the
system can be described in terms of single-particle energy
eigenstates, allowing some real analysis to be done.
particles. By ignoring particle interactions, the
system can be described in terms of single-particle energy
eigenstates, allowing some real analysis to be done.
However, a system of strictly noninteracting unperturbed particles
would be stuck into the initial energy eigenstate, or the initial
combination of such states, according to the Schrödinger equation.
To get such a system to settle down into a physically realistic
configuration, it is necessary to include the effects of the
unavoidable real life perturbations, (molecular motion of the
containing box, ambient electromagnetic field, cosmic rays, whatever.)
The effects of such small random perturbations will be accounted for
using reasonable assumptions. In particular, it will be assumed that
they tend to randomly stir up things a bit over time, taking the
system out of any physically unlikely state it may be stuck in and
making it settle down into the macroscopically stable one, called
“thermal equilibrium.”
Subsections
![]()