| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
11.7 The Basic Thermodynamic Variables
This section introduces the most important basic players in
thermodynamics.
The primary thermodynamic property introduced so far is the
temperature. Recall that temperature is a measure of the hotness of
the substance, a measure of how eager it is to dump energy onto other
systems. Temperature is called an “intensive variable;“ it is the same for two systems that differ
only in size.
The total number of particles  or the total volume of their box
or the total volume of their box  are not intensive variables; they are “extensive variables,“ variables that increase in value
proportional to the system size. Often, however, you are only
interested in the properties of your substance, not the amount. In
that case, intensive variables can be created by taking ratios of the
extensive ones; in particular,
are not intensive variables; they are “extensive variables,“ variables that increase in value
proportional to the system size. Often, however, you are only
interested in the properties of your substance, not the amount. In
that case, intensive variables can be created by taking ratios of the
extensive ones; in particular, 

 is an intensive variable called
the “particle density.” It is the number of particles per unit
volume. If you restrict your attention to only one half of your box
with particles, the particle density is still the same, with half the
particles in half the volume.
is an intensive variable called
the “particle density.” It is the number of particles per unit
volume. If you restrict your attention to only one half of your box
with particles, the particle density is still the same, with half the
particles in half the volume.
Note that under equilibrium conditions, it suffices to know the
temperature and particle density to fully fix the state that a given
system is in. More generally, the rule is that:
Two intensive variables must be known to fully determine the
intensive properties of a simple substance in thermal equilibrium.
(To be precise, in a two-phase equilibrium like a liquid-vapor
mixture, pressure and temperature are related, and would not be
sufficient to determine something like net specific volume.
They do still suffice to determine the specific volumes of the liquid
and vapor parts individually, in any case.) If the amount of
substance is also desired, knowledge of at least one extensive
variable is required, making three variables that must be known in
total.
Since the number of particles will have very large values, for
macroscopic work the particle density is often not very convenient,
and somewhat differently defined, but completely equivalent variables
are used. The most common are the (mass) “density” 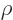 , found by multiplying the particle
density with the single-particle mass
, found by multiplying the particle
density with the single-particle mass  ,
, 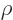

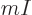

 , or its reciprocal, the “specific volume”
, or its reciprocal, the “specific volume” 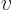



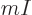 . The density is the
system mass per unit system volume, and the specific volume is the
system volume per unit system mass.
. The density is the
system mass per unit system volume, and the specific volume is the
system volume per unit system mass.
Alternatively, to keep the values for the number of particles in
check, they may be expressed in “moles,” multiples of Avogadro’s number
That produces the “molar density” 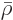



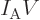 and “molar specific volume”
and “molar specific volume” 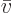

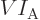

 . In
thermodynamic textbooks, the use of kilo mol (kmol) instead of mol has
become quite standard (but then, so has the use of kilo Newton instead
of Newton.) The conversion factor between molar and nonmolar specific
quantities is called the “molar mass”
. In
thermodynamic textbooks, the use of kilo mol (kmol) instead of mol has
become quite standard (but then, so has the use of kilo Newton instead
of Newton.) The conversion factor between molar and nonmolar specific
quantities is called the “molar mass” 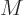 ; it is applied according to its units of
kg/kmol. Note that thermo books for engineers may misname
; it is applied according to its units of
kg/kmol. Note that thermo books for engineers may misname 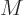 to be
the “molecular mass”. The numerical value of the molar mass is
roughly the total number of protons and neutrons in the nuclei of a
single molecule; in fact, the weird number of particles given by
Avogadro’s number was chosen to achieve this.
to be
the “molecular mass”. The numerical value of the molar mass is
roughly the total number of protons and neutrons in the nuclei of a
single molecule; in fact, the weird number of particles given by
Avogadro’s number was chosen to achieve this.
So what else is there? Well, there is the energy of the system. In
view of the uncertainty in energy, the appropriate system energy is
defined as the expectation value,
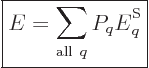 |
(11.6) |
where 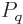 is the canonical probability of (11.4),
(11.5). Quantity
is the canonical probability of (11.4),
(11.5). Quantity 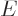 is called the “internal energy.” In engineering thermodynamics books, it is
usually indicated by
is called the “internal energy.” In engineering thermodynamics books, it is
usually indicated by  , but this is physics. The intensive
equivalent
, but this is physics. The intensive
equivalent 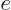 is found by dividing by the system mass;
is found by dividing by the system mass; 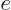

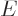

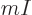 . Note the convention of indicating extensive variables
by a capital and their intensive value per unit mass with the
corresponding lower case letter. A specific quantity on a molar basis
is lower case with a bar above it.
. Note the convention of indicating extensive variables
by a capital and their intensive value per unit mass with the
corresponding lower case letter. A specific quantity on a molar basis
is lower case with a bar above it.
As a demonstration of the importance of the partition function
mentioned in the previous section, if the partition function
(11.5) is differentiated with respect to temperature, you get
(The volume of the system should be held constant in order that the
energy eigenfunctions do not change.) Dividing both sides by 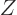 turns the derivative in the left hand side into that of the logarithm
of
turns the derivative in the left hand side into that of the logarithm
of 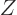 , and the sum in the right hand side into the internal
energy
, and the sum in the right hand side into the internal
energy 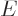 , and you get
, and you get
 |
(11.7) |
Next there is the “pressure” 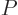 , being the force with which the substance
pushes on the surfaces of the box it is in per unit surface area. To
identify
, being the force with which the substance
pushes on the surfaces of the box it is in per unit surface area. To
identify 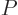 quantum mechanically, first consider a system in a single
energy eigenfunction
quantum mechanically, first consider a system in a single
energy eigenfunction  for certain. If the volume of the box is
slightly changed, there will be a corresponding slight change in the
energy eigenfunction
for certain. If the volume of the box is
slightly changed, there will be a corresponding slight change in the
energy eigenfunction  , (the boundary conditions of the
Hamiltonian eigenvalue problem will change), and in particular its
energy will slightly change. Energy conservation requires that the
change in energy
, (the boundary conditions of the
Hamiltonian eigenvalue problem will change), and in particular its
energy will slightly change. Energy conservation requires that the
change in energy 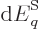 is offset by the work done by the
containing walls on the substance. Now the work done by the wall
pressure on the substance equals
is offset by the work done by the
containing walls on the substance. Now the work done by the wall
pressure on the substance equals
(The force is pressure times area and is normal to the area; the work
is force times displacement in the direction of the force; combining
the two, area times displacement normal to that area gives change in
volume. The minus sign is because the displacement must be inwards
for the pressure force on the substance to do positive work.) So for
the system in a single eigenstate, the pressure equals 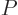

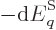

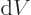 . For a real system with uncertainty in
energy, the pressure is defined as the expectation value:
. For a real system with uncertainty in
energy, the pressure is defined as the expectation value:
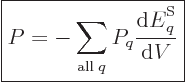 |
(11.8) |
It may be verified by simple substitution that this, too may be obtained
from the partition function, now by differentiating with respect to
volume keeping temperature constant:
 |
(11.9) |
While the final quantum mechanical definition of the pressure
is quite sound, it should be pointed out that the original definition
in terms of force was very artificial. And not just because force is
a poor quantum variable. Even if a system in a single eigenfunction
could be created, the walls of the system would have to be idealized
to assume that the energy change equals the work 
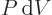 .
For example, if the walls of the box would consist of molecules that
were hotter than the particles inside, the walls too would add energy
to the system, and take it out of its single energy eigenstate to
boot. And even macroscopically, for pressure times area to be the
force requires that the system is in thermal equilibrium. It would
not be true for a system evolving in a violent way.
.
For example, if the walls of the box would consist of molecules that
were hotter than the particles inside, the walls too would add energy
to the system, and take it out of its single energy eigenstate to
boot. And even macroscopically, for pressure times area to be the
force requires that the system is in thermal equilibrium. It would
not be true for a system evolving in a violent way.
Often a particular combination of the variables defined above is very
convenient; the“enthalpy” 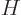 is defined as
is defined as
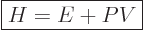 |
(11.10) |
Enthalpy is not a fundamentally new variable, just a combination of
existing ones.
Assuming that the system evolves while staying at least approximately
in thermal equilibrium, the “first law of thermodynamics” can be stated macroscopically as
follows:
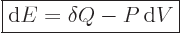 |
(11.11) |
In words, the internal energy of the system changes by the amount
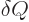 of heat added plus the amount
of heat added plus the amount 
 of work done on
the system. It is just energy conservation expressed in thermodynamic
terms. (And it assumes that other forms of energy than internal
energy and work done while expanding can be ignored.)
of work done on
the system. It is just energy conservation expressed in thermodynamic
terms. (And it assumes that other forms of energy than internal
energy and work done while expanding can be ignored.)
Note the use of a straight 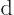 for the changes in internal energy
for the changes in internal energy
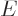 and volume
and volume  , but a
, but a  for the heat energy added.
It reflects that
for the heat energy added.
It reflects that 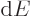 and
and  are changes in properties of
the system, but
are changes in properties of
the system, but 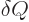 is not;
is not; 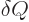 is a small amount of
energy exchanged between systems, not a property of any system. Also
note that while popularly you might talk about the heat within a
system, it is standard in thermodynamics to refer to the thermal
energy within a system as internal energy, and reserve the term
“heat” for exchanged thermal energy.
is a small amount of
energy exchanged between systems, not a property of any system. Also
note that while popularly you might talk about the heat within a
system, it is standard in thermodynamics to refer to the thermal
energy within a system as internal energy, and reserve the term
“heat” for exchanged thermal energy.
Just two more variables. The “specific heat at constant volume” 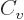 is defined as the heat that must be added to the substance for each
degree temperature change, per unit mass and keeping the volume
constant. In terms of the first law on a unit mass basis,
is defined as the heat that must be added to the substance for each
degree temperature change, per unit mass and keeping the volume
constant. In terms of the first law on a unit mass basis,
it means that 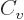 is defined as
is defined as 

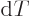 when
when
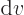
 0. So
0. So 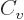 is the derivative of the specific
internal energy
is the derivative of the specific
internal energy 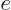 with respect to temperature. To be specific,
since specifying
with respect to temperature. To be specific,
since specifying 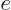 normally requires two intensive variables,
normally requires two intensive variables,
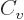 is the partial derivative of
is the partial derivative of 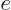 keeping specific volume
constant:
keeping specific volume
constant:
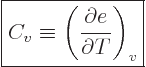 |
(11.12) |
Note that in thermodynamics the quantity being held constant while
taking the partial derivative is shown as a subscript to parentheses
enclosing the derivative. You did not see that in calculus, but that
is because in mathematics, they tend to choose a couple of independent
variables and stick with them. In thermodynamics, two independent
variables are needed, (assuming the amount of substance is a given),
but the choice of which two changes all the time. Therefore, listing
what is held constant in the derivatives is crucial.
The specific heat at constant pressure 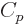 is defined similarly as
is defined similarly as
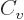 , except that pressure, instead of volume, is being held
constant. According to the first law above, the heat added is now
, except that pressure, instead of volume, is being held
constant. According to the first law above, the heat added is now
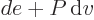 and that is the change in enthalpy
and that is the change in enthalpy 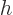

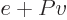 .
There is the first practical application of the enthalpy already! It
follows that
.
There is the first practical application of the enthalpy already! It
follows that
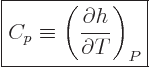 |
(11.13) |
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.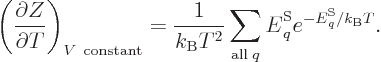
![]() ,
,![]()
![]()
![]() ,
,![]() i
i![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.