|
|
|
|
|
Next: 11.6 Low Temperature Behavior |
|
The particle energy distribution functions in the previous section were derived assuming that the energy is given. In quantum-mechanical terms, it was assumed that the energy had a definite value. However, that cannot really be right, for one because of the energy-time uncertainty principle.
Assume for a second that a lot of boxes of particles are carefully prepared, all with a system energy as precise as it can be made. And that all these boxes are then stacked together into one big system. In the combined system of stacked boxes, the energy is presumably quite unambiguous, since the random errors are likely to cancel each other, rather than add up systematically. In fact, simplistic statistics would expect the relative error in the energy of the combined system to decrease like the square root of the number of boxes.
But for the carefully prepared individual boxes, the future of their lack of energy uncertainty is much bleaker. Surely a single box in the stack may randomly exchange a bit of energy with the other boxes. Of course, when a box acquires much more energy than the others, the exchange will no longer be random, but almost certainly go from the hotter box to the cooler ones. Still, it seems unavoidable that quite a lot of uncertainty in the energy of the individual boxes would result. The boxes still have a precise temperature, being in thermal equilibrium with the larger system, but no longer a precise energy.
Then the appropriate way to describe the individual boxes is no longer
in terms of given energy, but in terms of probabilities. The proper
expression for the probabilities is deduced
in
derivation {D.58}. It turns out that when the
temperature ![]() ,
,![]()
canonical probability distribution.Feynman [18, p. 1] calls it the summit of statistical mechanics.
The exponential by itself is called the “Boltzmann factor.” The normalization factor ![]() ,
,
The canonical probability distribution conforms to the fundamental
assumption of quantum statistics that eigenfunctions of the same
energy have the same probability. However, it adds that for system
eigenfunctions with different energies, the higher energies are less
likely. Massively less likely, to be sure, because the system energy
![]()
![]()
![\begin{figure}\centering
{}%
\setlength{\unitlength}{1pt}
\begin{picture}(4...
...\%}}
\put(344.5,-11){\makebox(0,0)[b]{\small 36\%}}
\end{picture}
\end{figure}](img2359.gif) |
So, what happens to the simple model system from section 11.3 when the energy is no longer certain, and instead the probabilities are given by the canonical probability distribution? The answer is in the middle graphic of figure 11.7. Note that there is no longer a need to limit the displayed energies; the strong exponential decay of the Boltzmann factor takes care of killing off the high energy eigenfunctions. The rapid growth of the number of eigenfunctions does remain evident at lower energies where the Boltzmann factor has not yet reached enough strength.
There is still an oblique energy line in figure 11.7, but
it is no longer limiting energy; it is merely the energy at the most
probable shelf occupation numbers. Equivalently, it is the
expectation energy
of the system, defined following
the ideas of chapter 4.4.1 as
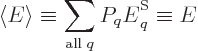
In thermodynamics, the expectation energy is called the
internal energy
and indicated by ![]()
![]() .
.![]() ,
,![]()
Figure 11.7 also shows the shelf occupation number
probabilities if the example 64 particles are not distinguishable, but
identical bosons or identical fermions. The most probable shelf
numbers are not the same, since bosons and fermions have different
numbers of eigenfunctions than distinguishable particles, but as the
figure shows, the effects are not dramatic at the shown temperature,
![]()
![]()