|
|
|
|
|
Next: 11.3 How Many System Eigenfunctions? |
|
The purpose of this section is to describe the generic form of the energy eigenfunctions of a system of weakly interacting particles.
The total number of particles will be indicated by ![]() .
.![]()
![]()
![]() .
.
The basic case is that of noninteracting particles in a box, like
discussed in chapter 6.2. For such particles the
single-particle eigenfunctions take the spatial form
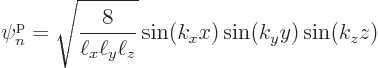
wave number components.Different values for these constants correspond to different single-particle eigenfunctions, with single-particle energy
The single-particle eigenfunctions do not always correspond to a particle in a box. For example, particles caught in a magnetic trap, like in the Bose-Einstein condensation experiments of 1995, might be better described using harmonic oscillator eigenfunctions. Or the particles might be restricted to move in a lower-dimensional space. But a lot of the formulae you can find in literature and in this chapter are in fact derived assuming the simplest case of noninteracting particles in a roomy box.
The details of the single-particle energy eigenfunctions are not
really that important in this chapter. What is more interesting are
the energy eigenfunctions ![]()
![]() ,
,
As long as the interactions between the particles are weak, energy
eigenfunctions of the complete system can be found as products of the
single-particle ones. As an important example, at absolute zero
temperature, all particles will be in the single-particle ground state
![]() ,
,
Statistical thermodynamics, in any case, is much more interested in
temperatures that are not zero. Then the system will not be in the
ground state, but in some combination of system eigenfunctions of
higher energy. As a completely arbitrary example of such a system
eigenfunction, take the following one, describing ![]()
![]()
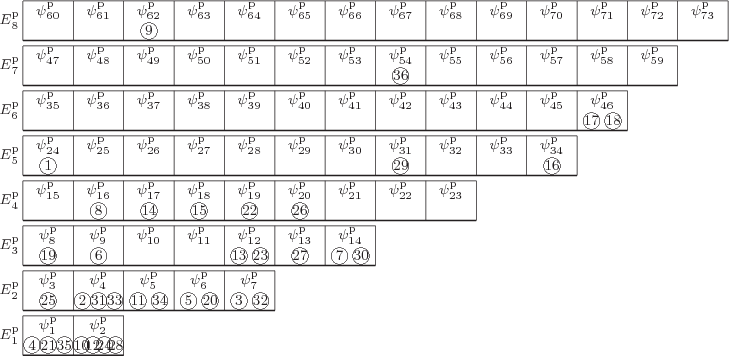 |
To understand the arguments in this chapter, it is essential to
visualize the system energy eigenfunctions as in figure
11.1. In this figure the single-particle states are shown
as boxes, and the particles that are in those particular
single-particle states are shown inside the boxes. In the example,
particle 1 is inside the ![]()
![]()
To simplify the analysis, in the figure single-particle eigenstates of
about the same energy have been grouped together on
shelves.
(As a consequence, a subscript to a
single-particle energy ![]()
![]()
![]() ,
,
Of course, in normal nonnano applications, the number of particles
will be astronomically larger than 36 particles; the example is just a
small illustration. Even a millimol of particles means on the order
of 1![]()
Next, note that you are not going to have something like 1![]()
Consider first the case that the ![]()
2” and “5in the particles changes the picture.
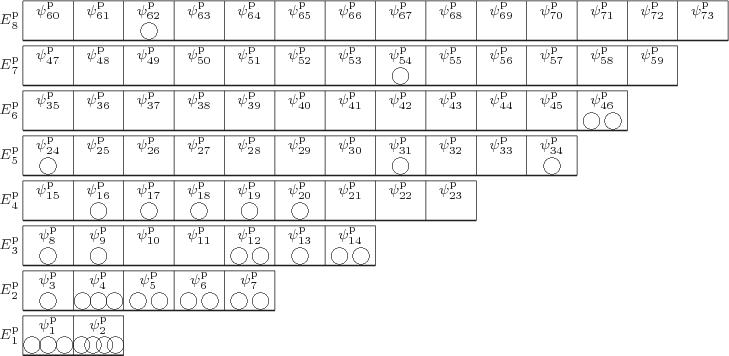 |
As chapter 5.7 explained, to eliminate the problem that exchanging particles 2 and 5 changes the wave function, the original and exchanged wave functions must be combined together. And to eliminate the problem for any two particles, all wave functions that can be obtained by merely swapping numbers must be combined together equally into a single wave function multiplied by a single undetermined coefficient. In terms of figure 11.1, we need to combine the wave functions with all possible permutations of the numbers inside the particles into one. And if all permutations of the numbers are equally included, then those numbers no longer add any nontrivial additional information; they may as well be left out. That makes the pictorial representation of an example system wave function for identical bosons as shown in figure 11.2.
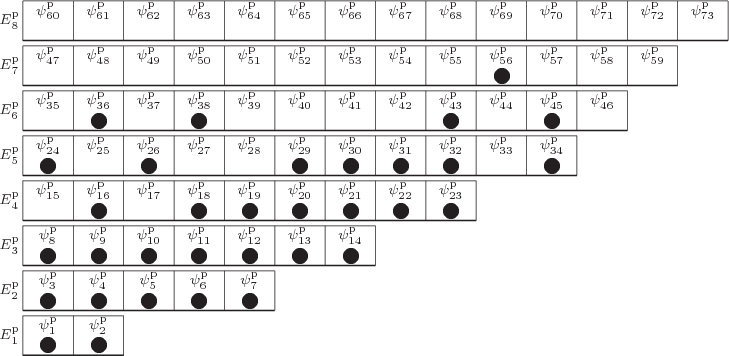 |
For identical fermions, the situation is similar, except that the
different wave functions must be combined with equal or opposite sign,
depending on whether it takes an odd or even number of particle swaps
to turn one into the other. And such wave functions only exist if the
![]()
Looking at the example pictorial representations for systems of bosons
and fermions, it may not be surprising that such particles are often
called “indistinguishable.“ Of course, in classical
quantum mechanics, there is still an electron 1, an electron 2,
etcetera; they are mathematically distinguished. Still, it is
convenient to use the term distinguishable
for
particles for which the symmetrization requirements can be ignored.
The prime example is the atoms of an ideal gas in a box; almost by definition, the interactions between such atoms are negligible. And that allows the quantum results to be referred back to the well-understood properties of ideal gases obtained in classical physics. Probably you would like to see all results follow naturally from quantum mechanics, not classical physics, and that would be very nice indeed. But it would be very hard to follow up on. As Baierlein [4, p. 109] notes, real-life physics adopts whichever theoretical approach offers the easiest calculation or the most insight. This book’s approach really is to formulate as much as possible in terms of the quantum-mechanical ideas discussed here. But do be aware that it is a much more messy world when you go out there.