|
|
|
|
|
Next: 6.3 Density of States |
|
As the previous section noted, the objective is to understand systems of noninteracting particles stuck in a closed, impenetrable, box. To do so, the key question is what are the single-particle quantum states, or energy eigenfunctions, for the particles. They will be discussed in this section.
The box will be taken to be rectangular, with its sides aligned with
the coordinate axes. The lengths of the sides of the box will be
indicated by ![]() ,
,![]() ,
,![]()
The single-particle energy eigenfunctions for such a box were derived
in chapter 3.5 under the guise of a pipe with a rectangular
cross section. The single-particle energy eigenfunctions are:
However, the precise form of the eigenfunctions is not really that
important here. What is important is how many there are and what
energy they have. That information can be summarized by plotting the
allowed wave numbers in a ![]()
Each point in this wave number space
corresponds to
one spatial single-particle state. The coordinates ![]() ,
,![]() ,
,![]()
![]()
One more point must be made. The single-particle energy
eigenfunctions described above are spatial states. Particles
with nonzero spin, which includes all fermions, can additionally
have different spin in whatever is chosen to be the
![]() -
-![]() ,
,spin-up” and a “spin-down
version of
each spatial energy eigenfunction:
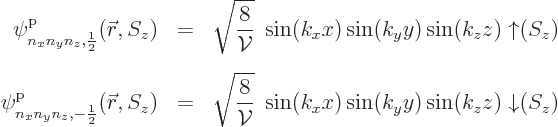
In general, if the particles have spin ![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ,
,
Key Points
- Each single particle state is characterized by a set of three
wave numbers,
and ,
.
- Each point in the
wave number spacefigure 6.1 corresponds to one specific spatial single-particle state.
- The distance of the point from the origin is a measure of the energy of the single-particle state.
- In the presence of nonzero particle spin
each point in wave number space corresponds to ,
separate single-particle states that differ in the spin in the chosen direction. For photons, make that -
instead of .