| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
A.21 Photon type 2 wave function
In quantum mechanics, photons are the particles of the electromagnetic
field. To actually use photons, something like a wave function for
them is needed. But that is not quite trivial for a purely
relativistic particle with zero rest mass like the photon. That is
the primary topic of this addendum. It will be assumed throughout
that the photon is in empty space.
A.21.1 The wave function
To see the problem with a photon wave function, a review of the wave
function of the nonrelativistic electron is useful, chapters
3.1 and 5.5.1. The electron wave function
can be written as a vector with two components:
This wave function takes on two different meanings
-
1.
- It gives the probability per unit volume of finding the electron
at a given position with a given spin. For example,
 gives the probability of finding the
electron with spin-up in an vicinity of infinitesimal volume
gives the probability of finding the
electron with spin-up in an vicinity of infinitesimal volume
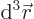 around position
around position 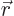 . That is the Born statistical
interpretation.
. That is the Born statistical
interpretation.
-
2.
- It is the unobservable function that nature seems to use to do
its quantum
computations
of how physics behaves.
Now a wave function of type 1 is not really meaningful for a photon.
What would it mean, find a photon? Since the photon has no rest mass,
you cannot bring them to a halt: there would be nothing left. And
anything you do to try to localize the electromagnetic field is likely
to just produce new photons. (To be sure, with some effort something
can be done towards a meaningful wave function of type 1, e.g. [Sype,
J.E. 1995 Phys. Rev. A 52, 1875]. It would have two components
like the electron, since the photon has two independent spin states.
But wave functions of that type are not widely accepted, nor useful
for the purposes here.)
So what? A wave function of type 1 is not that great anyway. For
one, it only defines the magnitudes of the components of the wave
function. If you only define the magnitude of a complex function, you
define only half of it. True, even as a type 2 wave function the
classical electron wave function is not quite unique. You can still
multiply either component by a factor  , with
, with
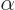 a real constant, without changing any of the physics. But
that is not by far as bad as completely ignoring everything else
besides the magnitude.
a real constant, without changing any of the physics. But
that is not by far as bad as completely ignoring everything else
besides the magnitude.
Furthermore, relativistic quantum mechanics has discovered that what
we call an electron is something cloaked in a cloud of virtual
particles. It is anybody’s guess what is inside that cloak, but
it will not be anything resembling what we would call an electron. So
what does it really mean, finding an electron within an infinitesimal
volume around a point? What happens to that cloak? And to really
locate an electron in an infinitesimal volume requires infinite
energy. If you try to locate the electron in a region that is small
enough, you are likely to just create additional electron-positron
pairs much like for photons.
For most practical purposes, classical physics understands the
particle behavior of electrons very well, but not their wave behavior.
Conversely, it understands the wave behavior of photons very well, but
not their particle behavior. But when you go to high enough energies,
that distinction becomes much less obvious.
The photon most definitely has a wave function of type 2 above. In
quantum electrodynamics, it may simply be called the photon wave
function, [24, p. 240]. However, since the term already
seems to be used for type 1 wave functions, this book will use the
term “photon type 2 wave function.” It may not tell you where to find
that elusive photon, but you will definitely need it to figure out how
that photon interacts with, say, an electron.
What the type 2 wave function of the photon is can be guessed readily
from classical electromagnetics. After all, the photon is supposed to
be the particle of the electromagnetic field. So, consider first
electrostatics. In classical electrostatics the forces on charged
particles are described by an electric force per unit charge
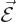 . That is called the electric field.
. That is called the electric field.
But quantum mechanics uses potentials, not forces. For example, the
solution of the hydrogen atom of chapter 4.3 used a
potential energy of the electron  . In electrostatics, this
potential energy is written as
. In electrostatics, this
potential energy is written as 

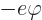 where
where 
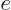 is the
charge of the electron and
is the
charge of the electron and 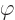 is called the electrostatic
potential. This potential is not directly observable nor unique; you
can add any constant to it without changing the observed physics.
is called the electrostatic
potential. This potential is not directly observable nor unique; you
can add any constant to it without changing the observed physics.
Clearly, an unobservable function 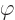 for the electromagnetic
field sounds much like a wave function for the particle of that field,
the photon. But actually, the electrostatic potential
for the electromagnetic
field sounds much like a wave function for the particle of that field,
the photon. But actually, the electrostatic potential 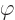 is
only part of it. In classical electromagnetics, there is not just an
electric field
is
only part of it. In classical electromagnetics, there is not just an
electric field 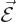 , there is also a magnetic field
, there is also a magnetic field
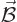 . It is known that this magnetic field can be represented
by a so-called
. It is known that this magnetic field can be represented
by a so-called vector potential
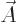 .
.
The following relationships give the electric and magnetic fields in
terms of these potentials:
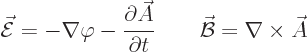 |
(A.86) |
Here the operator
is called nabla or del. As an example, for the  components of the
fields:
components of the
fields:
When both potentials are allowed for, the nonuniqueness becomes much
larger. In particular, for any arbitrary function 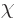 of position
and time, you can find two different potentials
of position
and time, you can find two different potentials 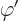 and
and 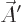 that produce the exact same electric and magnetic fields as
that produce the exact same electric and magnetic fields as 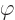 and
and 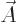 . These potentials are given by
. These potentials are given by
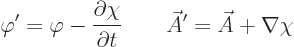 |
(A.87) |
This indeterminacy in potentials is the famous “gauge
property” of the electromagnetic field.
Finally, it turns out that classical relativistic mechanics likes to
combine the four scalar potentials in a four-dimensional vector, or
four-vector, chapter 1.3.2:
That is the one. Quantum mechanics takes a four-vector potential of
this form to be the type 2 wave function of the photon
![${\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{2.5pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over A}_{\kern-1pt\gamma}$](img4329.gif) . It keeps the gauge property
(A.87) for this wave function. However, note the following
important caveat:
. It keeps the gauge property
(A.87) for this wave function. However, note the following
important caveat:
The photon wave function ![${\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{2.5pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over A}_{\kern-1pt\gamma}$](img4329.gif) should not be
confused with the classical four-potential
should not be
confused with the classical four-potential ![${\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{2.5pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over A}$](img174.gif) .
.
Wave functions are in general complex. The classical four-potential,
and especially its physically observable derivatives, the electric and
magnetic fields, must be real. Indeed, according to quantum
mechanics, observable quantities correspond to eigenvalues of
Hermitian operators, not to wave functions. What the operators of the
observable electric and magnetic fields are will be discussed in
addendum {A.23}.
A.21.2 Simplifying the wave function
To use the photon wave function in practical applications, it is
essential to simplify it. That can be done by choosing a clever gauge
function 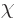 in the gauge property (A.87).
in the gauge property (A.87).
One very helpful simplification is to choose 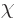 so that
so that
 |
(A.88) |
where 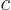 is the speed of light. This is called the “Lorenz condition.” A corresponding gauge function is a
“Lorenz gauge.” The reason why the Lorenz condition is a good
one is because all observers in inertial motion will agree it is true.
(You can crunch that out using the Lorentz transform as given in
chapter 1.2.1 (1.6). The four-vector
is the speed of light. This is called the “Lorenz condition.” A corresponding gauge function is a
“Lorenz gauge.” The reason why the Lorenz condition is a good
one is because all observers in inertial motion will agree it is true.
(You can crunch that out using the Lorentz transform as given in
chapter 1.2.1 (1.6). The four-vector
![${\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{2.5pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over A}_{\kern-1pt\gamma}$](img4329.gif) transforms the same way as the four-vector
transforms the same way as the four-vector
![$\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{1pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over r}
\kern-1.3pt$](img4331.gif) . However, you will need to use the inverse transform for
one of the two four-vectors. Alternatively, those familiar with index
notation as briefly described in chapter 1.2.5 recognize
the Lorenz condition as being simply
. However, you will need to use the inverse transform for
one of the two four-vectors. Alternatively, those familiar with index
notation as briefly described in chapter 1.2.5 recognize
the Lorenz condition as being simply 
 0. That is unchanged going from one observer to the next,
because the upper index transforms under the Lorentz transform and the
lower index under the inverse Lorentz transform.)
0. That is unchanged going from one observer to the next,
because the upper index transforms under the Lorentz transform and the
lower index under the inverse Lorentz transform.)
To achieve the Lorenz condition, assume an initial wave function
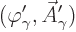 that does not satisfy it. Then
plug the gauge property (A.87) into the Lorenz condition
above. That shows that the needed gauge function
that does not satisfy it. Then
plug the gauge property (A.87) into the Lorenz condition
above. That shows that the needed gauge function 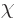 must satisfy
must satisfy
This equation for 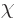 is called an inhomogeneous Klein-Gordon
equation. (More generically, it is called an inhomogeneous wave
equation.)
is called an inhomogeneous Klein-Gordon
equation. (More generically, it is called an inhomogeneous wave
equation.)
There is another reason why you want to satisfy the Lorenz condition.
The photon is a purely relativistic particle with zero rest mass.
Then following the usual ideas of quantum mechanics, in empty space
its wave function should satisfy the homogeneous Klein-Gordon
equation, {A.14} (A.43):
 |
(A.89) |
Unfortunately, that is not automatic. In general, gauge transforms
mess up this equation. However, as long as gauge transforms respect
the Lorenz condition, they also respect the Klein-Gordon equation.
So reasonably speaking, normal
photon wave functions,
the ones that do satisfy the Klein-Gordon equation, should be exactly
the ones that also satisfy the Lorenz condition.
Maxwell’s classical electromagnetics provides additional support
for that idea. There the Klein-Gordon equation for the potentials
also requires that the Lorenz condition is satisfied,
{A.37}.
Since the inhomogeneous Klein-Gordon equation for the gauge function
 is second order in time, it still leaves two initial conditions
to be chosen. These can be chosen such as to make the initial values
for
is second order in time, it still leaves two initial conditions
to be chosen. These can be chosen such as to make the initial values
for  and its time-derivative zero. That then makes
and its time-derivative zero. That then makes
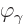 completely zero, because it satisfies the homogeneous
Klein-Gordon equation.
completely zero, because it satisfies the homogeneous
Klein-Gordon equation.
And so the fully simplified photon wave function becomes:
 |
(A.90) |
The final condition applies because of the Lorenz condition
(A.88). Using an expensive word, the final condition says
that 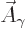 must be
must be solenoidal.
A gauge
function that makes 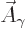 solenoidal is called a “Coulomb gauge.”
solenoidal is called a “Coulomb gauge.”
It should be noted that the Coulomb gauge is not Lorentz invariant. A
moving observer will not agree that the potential 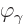 is
zero and that
is
zero and that 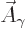 is solenoidal. In real life that means
that if you want to study a process in say a center-of-mass system,
first switch to that system and then assume the Coulomb gauge. Not
the other way around. The Coulomb-Lorenz gauge is too helpful not to
use, although that is possible, [24, p. 241].
is solenoidal. In real life that means
that if you want to study a process in say a center-of-mass system,
first switch to that system and then assume the Coulomb gauge. Not
the other way around. The Coulomb-Lorenz gauge is too helpful not to
use, although that is possible, [24, p. 241].
A.21.3 Photon spin
Now that the photon wave function has been simplified the photon spin
can be determined. Recall that for the electron, the two components
of the wave function correspond to its two possible values of the spin
angular momentum 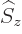 in the chosen
in the chosen  -direction. In particular,
-direction. In particular,
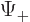 corresponds to
corresponds to 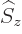

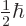 , and
, and
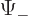 to
to 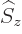

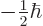 . Since the wave
function of the photon is a four-dimensional vector, at first it might
therefore look like the photon should have spin
. Since the wave
function of the photon is a four-dimensional vector, at first it might
therefore look like the photon should have spin 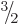 .
That would make
.
That would make 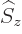 one of
one of 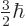 ,
,
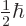 ,
, 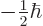 , or
, or 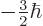 .
But that is not true.
.
But that is not true.
The simplified wave function (A.90) has only three
nontrivial components. And the gauge property requires that this
simplified wave function still describes all the physics. Since the
only nontrivial part left is the three-dimensional vector
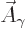 , the spin of the photon must be 1. The possible
values of the spin in the
, the spin of the photon must be 1. The possible
values of the spin in the  -direction
-direction 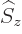 are
are 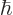 , 0,
and
, 0,
and 
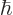 . The photon is a vector boson like discussed in
addendum {A.20}.
. The photon is a vector boson like discussed in
addendum {A.20}.
However, that is not quite the end of the story. There is still that
additional condition 
 0 to
satisfy. In principle this constraint allows another component of the
wave function to be eliminated. However, all three remaining
components are spatial ones. So it does not make much sense to
eliminate one and not the other. More importantly, it is known from
relativity that
0 to
satisfy. In principle this constraint allows another component of the
wave function to be eliminated. However, all three remaining
components are spatial ones. So it does not make much sense to
eliminate one and not the other. More importantly, it is known from
relativity that 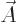 behaves like a normal three-dimensional
vector under rotations of the coordinate system, not like a
two-dimensional spinor like the electron wave function. That is
implicit in the fact that the complete four-vector transforms
according to the Lorentz transform, chapter 1.3.2. The
spin is really 1.
behaves like a normal three-dimensional
vector under rotations of the coordinate system, not like a
two-dimensional spinor like the electron wave function. That is
implicit in the fact that the complete four-vector transforms
according to the Lorentz transform, chapter 1.3.2. The
spin is really 1.
Still, the additional constraint does limit the angular momentum of
the photon. In particular, a photon does not have independent spin
and orbital angular momentum. The two are intrinsically linked. What
that means for the net angular momentum of photons is worked out in
subsection A.21.7.
For now it may already be noted that the photon has no state of zero
net angular momentum. A state of zero angular momentum needs to look
the same from all directions. That is a consequence of the
relationship between angular momentum and symmetry, chapter
7.3. Now the only vector wave functions that look the
same from all directions are of the form 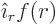 . Here
. Here
 is the distance from the origin around which the angular momentum
is measured and
is the distance from the origin around which the angular momentum
is measured and  the unit vector pointing away from the
origin. Such a wave function cannot satisfy the condition
the unit vector pointing away from the
origin. Such a wave function cannot satisfy the condition
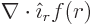
 0. That follows from applying the
divergence theorem for a sphere around the origin.
0. That follows from applying the
divergence theorem for a sphere around the origin.
A.21.4 Energy eigenstates
Following the rules of quantum mechanics, {A.14},
photon states of definite energy 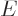 take the form
take the form
Here 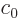 is an arbitrary constant. More importantly
is an arbitrary constant. More importantly
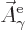 is the energy eigenfunction, which is
independent of time.
is the energy eigenfunction, which is
independent of time.
Substitution in the Klein-Gordon equation and cleaning up shows that
this eigenfunction needs to satisfy the eigenvalue problem,
{A.14},
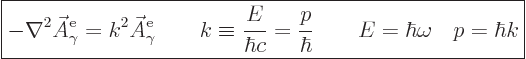 |
(A.91) |
Here 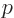 is the magnitude of the linear momentum of the photon. The
so-called Planck-Einstein relation gives the energy
is the magnitude of the linear momentum of the photon. The
so-called Planck-Einstein relation gives the energy 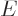 in terms of
the photon frequency
in terms of
the photon frequency 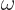 , while the de Broglie relation
gives the momentum
, while the de Broglie relation
gives the momentum 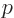 in terms of the photon wave number
in terms of the photon wave number 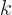 .
.
A.21.5 Normalization of the wave function
A classical wave function for a particle is normalized by demanding
that the square integral of the wave function is 1. That does not
work for a relativistic particle like the photon, since the
Klein-Gordon equation does not preserve the square integral of the
wave function, {A.14}.
However, the Klein-Gordon equation does preserve the following
integral, {D.36.1},
Reasonably speaking, you would expect this integral to be related to
the energy in the electromagnetic field. After all, what other scalar
physical quantity is there to be preserved?
Consider for a second the case that 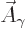 was a classical
potential
was a classical
potential 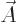 instead of a photon wave function. Then the above
integral can be rewritten in terms of the electric and magnetic fields
instead of a photon wave function. Then the above
integral can be rewritten in terms of the electric and magnetic fields
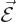 and
and 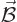 as, {D.36.1},
as, {D.36.1},
Now classical physics does not have photons of energy
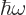 . All it has are electric and magnetic fields.
Then surely the integral above must be a measure for the energy in the
electromagnetic field? What is more logical than that the energy in
the electromagnetic field per unit volume would be given by the square
magnitudes of the electric and magnetic fields? No fields, no energy.
. All it has are electric and magnetic fields.
Then surely the integral above must be a measure for the energy in the
electromagnetic field? What is more logical than that the energy in
the electromagnetic field per unit volume would be given by the square
magnitudes of the electric and magnetic fields? No fields, no energy.
Of course, there needs to be an additional constant; the integral
above does not have units of energy. If you check, you find that the
permittivity of space
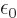
 8.85
10
8.85
10 C
C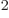 /J m has the right units to be the
constant. Actually, it turns out that the correct constant is
/J m has the right units to be the
constant. Actually, it turns out that the correct constant is
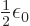 . But that is not a fundamental issue;
classical physics could just as well have defined
. But that is not a fundamental issue;
classical physics could just as well have defined 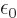 as half
of what it did.
as half
of what it did.
Now the photon wave function is not physically observable and does not
have to conform to the rules of classical physics. But if you have to
choose a normalization constant anway? Why not choose it so that what
classical physics would take to be the energy is in fact the correct
energy 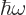 ? It is likely to simplify your life a lot.
? It is likely to simplify your life a lot.
So, the photon wave function normalization that will be used in this
book is:
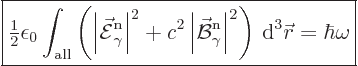 |
(A.92) |
Here 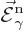 and
and 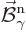 are what classical physics
would take to be the electric and magnetic fields for the normalized
photon energy eigenfunction
are what classical physics
would take to be the electric and magnetic fields for the normalized
photon energy eigenfunction 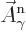 . Specifically,
. Specifically,
(To be sure, classical physics would take 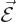 to be minus the time
derivative of the potential
to be minus the time
derivative of the potential 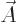 . But for an energy
eigenstate, the time derivative gives a simple factor
. But for an energy
eigenstate, the time derivative gives a simple factor 



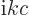 .) The functions
.) The functions 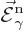 and
and
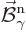 will be referred to as “unobservable
fields” to avoid confusion with the observable electric and
magnetic fields.
will be referred to as “unobservable
fields” to avoid confusion with the observable electric and
magnetic fields.
Assume that you start with an unnormalized energy eigenfunction
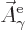 . Then the normalized functions are
usually most conveniently written as
. Then the normalized functions are
usually most conveniently written as
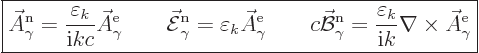 |
(A.93) |
Here the constant 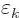 is to be found by substitution
into the normalization condition (A.92).
is to be found by substitution
into the normalization condition (A.92).
A.21.6 States of definite linear momentum
The simplest quantum states for photons are states of definite linear
momentum 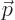 . And to make it even simpler, it will be assumed
that the
. And to make it even simpler, it will be assumed
that the  -axis is chosen in the direction of the linear momentum.
-axis is chosen in the direction of the linear momentum.
In that case, the photon wave function takes the form
Here  is a constant vector. That this wave function has
definite linear momentum
is a constant vector. That this wave function has
definite linear momentum 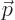 may be verified by applying the linear
momentum operator
may be verified by applying the linear
momentum operator 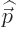

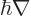

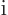 on it. And substitution into
the eigenvalue problem (A.91) verifies that it is an energy
eigenfunction.
on it. And substitution into
the eigenvalue problem (A.91) verifies that it is an energy
eigenfunction.
The vector  is not completely arbitrary; its
is not completely arbitrary; its  -component
must be zero. That is in order that
-component
must be zero. That is in order that
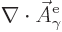 is zero as the Coulomb-Lorenz
gauge requires. So the wave function can be written as
is zero as the Coulomb-Lorenz
gauge requires. So the wave function can be written as
The bottom line is that there are only two independent states, even
though the wave function is a three-dimensional vector. The wave
function cannot have a component in the direction of motion. It may
be noted that the first term in the right hand side above is called a
wave that is “linearly polarized” in the  -direction. Similarly, the
second term is a wave that is linearly polarized in the
-direction. Similarly, the
second term is a wave that is linearly polarized in the  -direction.
There is no longitudinal polarization of photons possible.
-direction.
There is no longitudinal polarization of photons possible.
There is another useful way to write the wave function:
where 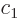 and
and 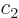 are constants. The first term in this
expression is called “right-circularly polarized.” It has angular momentum
are constants. The first term in this
expression is called “right-circularly polarized.” It has angular momentum 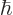 in
the
in
the  -direction. (To see why is a matter of rotating the
coordinate system around the
-direction. (To see why is a matter of rotating the
coordinate system around the  -axis, {A.20}.
The exponential does not change in such a rotation.) Similarly, the
second state has angular momentum
-axis, {A.20}.
The exponential does not change in such a rotation.) Similarly, the
second state has angular momentum 
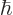 in the
in the
 -direction and is called left-circularly polarized. There is
no state with angular momentum zero in the
-direction and is called left-circularly polarized. There is
no state with angular momentum zero in the  -direction. In
fact, it is exactly the missing
-direction. In
fact, it is exactly the missing  -component of
-component of  that
would provide such a state, {A.20}.
that
would provide such a state, {A.20}.
There are still only two independent states. But another way of
thinking about that is that the spin angular momentum in the direction
of motion cannot be zero. The relative spin in the direction of
motion, 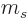

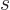 is called the “helicity.” It turns out that for a particle with zero rest mass
like the photon, the helicity can only be 1 (right handed) or -1 (left
handed), [24, p. 65].
is called the “helicity.” It turns out that for a particle with zero rest mass
like the photon, the helicity can only be 1 (right handed) or -1 (left
handed), [24, p. 65].
Note further that the angular momenta in the  and
and  directions
are uncertain. It so happens that the angular momentum in the
direction of motion commutes with all three components of linear
momentum, chapter 4.5.4. So it can have definite values.
But the
directions
are uncertain. It so happens that the angular momentum in the
direction of motion commutes with all three components of linear
momentum, chapter 4.5.4. So it can have definite values.
But the  and
and  angular momenta do not commute.
angular momenta do not commute.
For later use, it is necessary to normalize the wave function using
the procedure described in the previous subsection. To do so, it must
be assumed that the photon is in a periodic box of volume
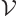 , like in chapter 6.17. In infinite space the
wave function cannot be normalized, as it does not become zero at
infinity. For the right-circularly polarized wave function as given
above,
, like in chapter 6.17. In infinite space the
wave function cannot be normalized, as it does not become zero at
infinity. For the right-circularly polarized wave function as given
above,
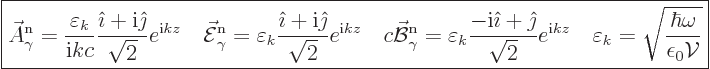 |
(A.94) |
In order to compare to the classical electromagnetic wave in chapter
7.7.1, another example is needed. This photon wave function
has its linear momentum in the  -direction, and it is linearly
polarized in the
-direction, and it is linearly
polarized in the  -direction. Then an unnormalized energy
eigenfunction is
-direction. Then an unnormalized energy
eigenfunction is
The normalized eigenfunction and unobservable fields are in that case
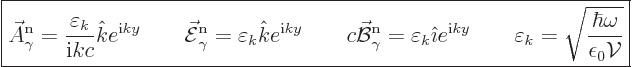 |
(A.95) |
Note that 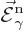 ,
, 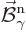 , and the linear
momentum are all orthogonal. That will reflect in the observable
fields associated with the photon state. For the circularly polarized
state, the electric and magnetic fields are not orthogonal. However,
the observable fields will be.
, and the linear
momentum are all orthogonal. That will reflect in the observable
fields associated with the photon state. For the circularly polarized
state, the electric and magnetic fields are not orthogonal. However,
the observable fields will be.
For a general direction of the wave motion and its linear
polarization, the above expession becomes
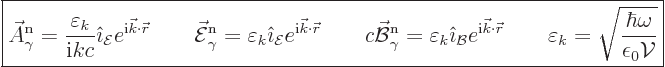 |
(A.96) |
Here 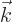 and the unit vectors
and the unit vectors 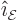 and
and


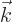
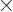
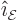

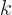 are all orthogonal
are all orthogonal
For convenience, the density of states as needed for Fermi’s
golden rule will be listed here. It was given earlier in chapter
6.3 (6.7) and 6.19:
A.21.7 States of definite angular momentum
It is often convenient to describe photons in terms of states of
definite net angular momentum. That makes it much easier to apply
angular momentum conservation in the emission of radiation by atoms or
atomic nuclei. Unfortunately, angular momentum states are a bit of a
mess compared to the linear momentum states of the previous
subsection. Fortunately, engineers are brave.
Before diving in, it is a good idea to look first at a spinless
particle. Assume that this hypothetical particle is in an energy
eigenstate. Also assume that this state has square orbital angular
momentum 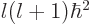 where
where  is called the azimuthal quantum
number. And that the state has orbital angular momentum in the
is called the azimuthal quantum
number. And that the state has orbital angular momentum in the
 -direction
-direction  where
where 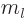 is called the magnetic quantum
number. Then according to quantum mechanics, chapter 4.2.3,
is called the magnetic quantum
number. Then according to quantum mechanics, chapter 4.2.3,
 must be a nonnegative integer and
must be a nonnegative integer and 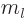 must be an integer no
larger in magnitude than
must be an integer no
larger in magnitude than  . Also, in spherical coordinates
. Also, in spherical coordinates
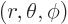 , figure 4.7, the angular
dependence of the energy eigenfunction must be given by the so-called
spherical harmonic
, figure 4.7, the angular
dependence of the energy eigenfunction must be given by the so-called
spherical harmonic 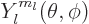 . If in addition the
particle is in empty space, the energy eigenfunction takes the general
form, {A.6},
. If in addition the
particle is in empty space, the energy eigenfunction takes the general
form, {A.6},
Here 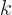 is a constant related to the energy of the particle and
whether it is relativistic or not, {A.14} (A.44).
Further
is a constant related to the energy of the particle and
whether it is relativistic or not, {A.14} (A.44).
Further 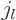 is the so-called “spherical Bessel function of
the first kind of order
is the so-called “spherical Bessel function of
the first kind of order  ,” {A.6}.
The parity of the eigenfunction is positive if
,” {A.6}.
The parity of the eigenfunction is positive if  is even and
negative if
is even and
negative if  is odd, {D.14}. The eigenfunction is
of order
is odd, {D.14}. The eigenfunction is
of order 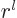 near the origin. That is only nonzero at the origin
near the origin. That is only nonzero at the origin

 0 if
0 if 
 0. That is important if there is, say, a
vanishingly small atom is located at the origin. All states except
0. That is important if there is, say, a
vanishingly small atom is located at the origin. All states except

 0 are virtually zero at such an atom. So the atom only has
a decent chance to interact with the particle if the particle is in a
state
0 are virtually zero at such an atom. So the atom only has
a decent chance to interact with the particle if the particle is in a
state 
 0. End discussion of the hypothetical spinless
particle.
0. End discussion of the hypothetical spinless
particle.
Now the photon is a particle with spin 1. Its wave function is
essentially a vector 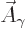 . The angular momentum states
and parity for such particles were discussed in {A.20}.
But the photon is a special case because it must be solenoidal, it
must satisfy
. The angular momentum states
and parity for such particles were discussed in {A.20}.
But the photon is a special case because it must be solenoidal, it
must satisfy 
 0. Normally, for
three-dimensional vectors you expect three types of angular momentum
states, like in {A.20}. But for the photon there are
only two types.
0. Normally, for
three-dimensional vectors you expect three types of angular momentum
states, like in {A.20}. But for the photon there are
only two types.
The two types of photon energy eigenfunctions with definite net
angular momentum are, {D.36.2} and with drums please,
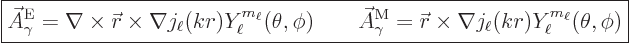 |
(A.97) |
Here  is the azimuthal quantum number of the net photon
angular momentum, orbital plus spin. And
is the azimuthal quantum number of the net photon
angular momentum, orbital plus spin. And 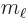 is the corresponding
net magnetic quantum number.
is the corresponding
net magnetic quantum number.
The azimuthal quantum number  is at least 1; the expressions
above produce zero for
is at least 1; the expressions
above produce zero for 
 0. (
0. (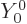 is just a constant
and the gradient of a radial function is in the direction of
is just a constant
and the gradient of a radial function is in the direction of
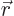 .) The photon energy is related to the wave number
.) The photon energy is related to the wave number 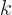 as
as
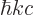 with
with 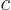 the speed of light, (A.91). That is
really the Planck-Einstein relation, because
the speed of light, (A.91). That is
really the Planck-Einstein relation, because  is the photon
frequency
is the photon
frequency 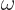 .
.
The parity of the electric multipole wave functions is negative if
 is odd and positive if
is odd and positive if  is even, {D.36.2.7}.
The parity of the magnetic multipole wave functions is exactly the
other way around. From that it can be seen, {D.36.2.8},
that magnetic multipole wave functions have orbital angular momentum
is even, {D.36.2.7}.
The parity of the magnetic multipole wave functions is exactly the
other way around. From that it can be seen, {D.36.2.8},
that magnetic multipole wave functions have orbital angular momentum


 . The electric ones have uncertainty in orbital
angular momentum, with nonzero probabilities for both
. The electric ones have uncertainty in orbital
angular momentum, with nonzero probabilities for both 

 and
and 

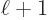 .
.
Atomic or nuclear transitions in which a photon in a state
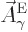 is emitted or absorbed are called “electric multipole” transitions. They are indicated as
E
is emitted or absorbed are called “electric multipole” transitions. They are indicated as
E transitions.
transitions.
In particular, for net angular momentum 
 1, they are called
1, they are called
 or electric dipole transitions. That is the normal kind.
However, as discussed in chapter 7.4, such transitions
may not be able to satisfy conservation of angular momentum and
parity. Since the photon in the state has
or electric dipole transitions. That is the normal kind.
However, as discussed in chapter 7.4, such transitions
may not be able to satisfy conservation of angular momentum and
parity. Since the photon in the state has 
 1, transitions in
which the atomic angular momentum changes by more than one unit cannot
be accomodated. Neither can transitions in which the atomic or
nuclear momentum parity does not change, because the
1, transitions in
which the atomic angular momentum changes by more than one unit cannot
be accomodated. Neither can transitions in which the atomic or
nuclear momentum parity does not change, because the  photon has odd parity.
photon has odd parity.
Such transitions may be accomodated by transitions in which photons in
different states are emitted or absorbed, using the photon angular
momenta and parities as noted above. Electric multipole transitions
with 
 2 are called
2 are called 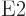 or electric quadrupole
transitions. Those with
or electric quadrupole
transitions. Those with 
 3 are
3 are 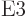 or electric
octupole ones, with
or electric
octupole ones, with 
 4
4 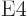 or electric
hexadecapole ones, with
or electric
hexadecapole ones, with 
 5
5 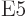 or electric
triakontadipole ones, for
or electric
triakontadipole ones, for 
 6
6 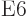 or electric
hexacontatetrapole ones and so on until your knowledge of latin and
greek powers of 2 runs out.
or electric
hexacontatetrapole ones and so on until your knowledge of latin and
greek powers of 2 runs out.
Similarly, transitions in which photons in a state
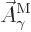 are emitted or absorbed are called “magnetic multipole transitions.” The same latin applies.
are emitted or absorbed are called “magnetic multipole transitions.” The same latin applies.
Like the states of definite linear momentum in the previous
subsection, the states of definite angular momentum cannot be
normalized in infinite space. To deal with that, it will be assumed
that the photon is confined inside a sphere of a very large radius
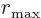 . As a
. As a boundary condition
on the
sphere, it will be assumed that the Bessel function is zero. In terms
of the wave functions, that works out to mean that the magnetic ones
are zero on the sphere, but only the radial component of the electric
ones is.
The normalized wave function and unobservable fields for electric
multipole photons are then, subsection A.21.5 and
{D.36},
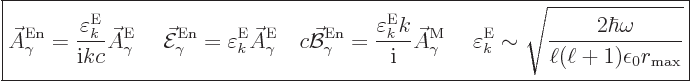 |
(A.98) |
(The expression for the magnetic field arises because for a solenoidal
vector 
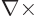


 , and
that produces a factor
, and
that produces a factor 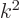 according to the energy eigenvalue
problem.)
according to the energy eigenvalue
problem.)
The normalized wave function and unobservable fields for magnetic
multipole photons are
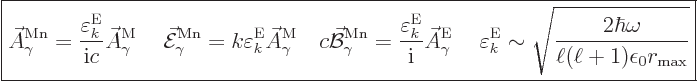 |
(A.99) |
Assume now that there is an atom or atomic nucleus at the origin that
interacts with the photon. An atom or nucleus is typically very small
compared to the wave length of the photon that it interacts with.
Phrased more appropriately, if 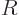 is the typical size of the atom or
nucleus, then
is the typical size of the atom or
nucleus, then 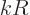 is typically small. The atom or nucleus is just a
tiny speck at the origin.
is typically small. The atom or nucleus is just a
tiny speck at the origin.
Now the wave functions 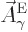 are larger at small radii
than the
are larger at small radii
than the 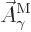 . In particular, the
. In particular, the
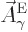 are of order
are of order 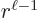 while the
while the
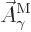 are of order
are of order 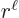 , one power of
, one power of  smaller. These powers of
smaller. These powers of  reflect the lowest measurable orbital
angular momentum of the states.
reflect the lowest measurable orbital
angular momentum of the states.
A glance at the unobservable fields of electric multipole photons
above then shows that for these photons, the field is primarily
electric at the atom or nucleus. And even the electric field will be
small unless 
 1, in other words, unless it is an electric dipole
photon.
1, in other words, unless it is an electric dipole
photon.
For the magnetic multipole photons, it is the magnetic field that
dominates at the atom or nucleus. And even that will be small unless

 1, which means a magnetic dipole photon. Note that the magnetic
field acts as if it had one unit or orbital angular momentum less than
the photon; the magnetic field is essentially the wave function of an
electric multipole photon.
1, which means a magnetic dipole photon. Note that the magnetic
field acts as if it had one unit or orbital angular momentum less than
the photon; the magnetic field is essentially the wave function of an
electric multipole photon.
For later reference, the density of states as needed for Fermi’s
golden rule will be listed here, {D.36.2.6}:
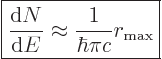 |
(A.100) |
This approximation applies for large cut-off radius
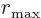 , which should always be valid.
, which should always be valid.
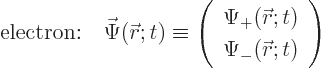
![]() ,
,![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]() .
.
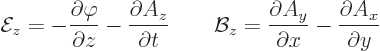
![]()
![]()
![]()
![]()
![]() .
.![\begin{displaymath}
{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{2.5pt}...
...(\begin{array}{c}\varphi/c\ A_x\ A_y\ A_z\end{array}\right)
\end{displaymath}](img4328.gif)
![]() .
..
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]() .
.![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() -
-![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
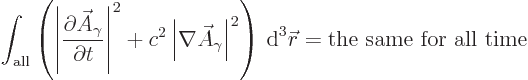
![]()
![]()
![]()
![]()
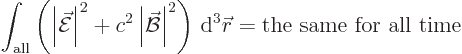
![]()
![]()
![]()
![]() /
/![]() .
.![]()
![]() ?
?![]() .
.![]() .
.![]() -
-![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() -
-![]() -
-![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()