3.1 The Re­vised Pic­ture of Na­ture

This sec­tion de­scribes the view quan­tum me­chan­ics has of na­ture, which is in terms of a mys­te­ri­ous func­tion called the “wave func­tion”.

Ac­cord­ing to quan­tum me­chan­ics, the way that the old New­ton­ian physics de­scribes na­ture is wrong if ex­am­ined closely enough. Not just a bit wrong. To­tally wrong. For ex­am­ple, the New­ton­ian pic­ture for a par­ti­cle of mass $m$ looks like fig­ure 3.1:

Fig­ure 3.1: The old in­cor­rect New­ton­ian physics.

The prob­lems? A nu­mer­i­cal po­si­tion for the par­ti­cle sim­ply does not ex­ist. A nu­mer­i­cal ve­loc­ity or lin­ear mo­men­tum for the par­ti­cle does not ex­ist.

What does ex­ist ac­cord­ing to quan­tum me­chan­ics is the so-called wave func­tion $\Psi(x,y,z;t)$. Its square mag­ni­tude, $\vert\Psi\vert^2$, can be shown as grey tones (darker where the mag­ni­tude is larger), as in fig­ure 3.2:

Fig­ure 3.2: The cor­rect quan­tum physics.

The phys­i­cal mean­ing of the wave func­tion is known as “Born's sta­tis­ti­cal in­ter­pre­ta­tion”: darker re­gions are re­gions where the par­ti­cle is more likely to be found if the lo­ca­tion is nar­rowed down. More pre­cisely, if ${\skew0\vec r}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $(x,y,z)$ is a given lo­ca­tion, then

$$\vert\Psi({\skew0\vec r};t)\vert^2 { \rm d}^3 {\skew0\vec r}$$ (3.1)

is the prob­a­bil­ity of find­ing the par­ti­cle within a small vol­ume, of size ${\rm d}^3{\skew0\vec r}$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\rm d}{x}{\rm d}{y}{\rm d}{z}$, around that given lo­ca­tion, if such a mea­sure­ment is at­tempted.

(And if such a po­si­tion mea­sure­ment is ac­tu­ally done, it af­fects the wave func­tion: af­ter the mea­sure­ment, the new wave func­tion will be re­stricted to the vol­ume to which the po­si­tion was nar­rowed down. But it will spread out again in time if al­lowed to do so af­ter­wards.)

The par­ti­cle must be found some­where if you look every­where. In quan­tum me­chan­ics, that is ex­pressed by the fact that the to­tal prob­a­bil­ity to find the par­ti­cle, in­te­grated over all pos­si­ble lo­ca­tions, must be 100% (cer­tainty):

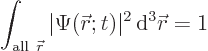$$\int_{{\rm all }{\skew0\vec r}} \vert\Psi({\skew0\vec r};t)\vert^2 { \rm d}^3 {\skew0\vec r}= 1$$ (3.2)

In other words, proper wave func­tions are nor­mal­ized, $\langle\Psi\vert\Psi\rangle$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1.

The po­si­tion of macro­scopic par­ti­cles is typ­i­cally very much nar­rowed down by in­ci­dent light, sur­round­ing ob­jects, ear­lier his­tory, etcetera. For such par­ti­cles, the blob size of the wave func­tion is ex­tremely small. As a re­sult, claim­ing that a macro­scopic par­ti­cle, is, say, at the cen­ter point of the wave func­tion blob may be just fine in prac­ti­cal ap­pli­ca­tions. But when you are in­ter­ested in what hap­pens on very small scales, the nonzero blob size can make a big dif­fer­ence.

In ad­di­tion, even on macro­scopic scales, po­si­tion can be ill de­fined. Con­sider what hap­pens if you take the wave func­tion blob apart and send half to Mars and half to Venus. Quan­tum me­chan­ics al­lows it; this is what hap­pens in a scat­ter­ing ex­per­i­ment. You would pre­sum­ably need to be ex­tremely care­ful to do it on such a large scale, but there is no fun­da­men­tal the­o­ret­i­cal ob­jec­tion in quan­tum me­chan­ics. So, where is the par­ti­cle now? Hid­ing on Mars? Hid­ing on Venus?

Or­tho­dox quan­tum me­chan­ics says: nei­ther. It will pop up on one of the two plan­ets if mea­sure­ments force it to re­veal its pres­ence. But un­til that mo­ment, it is just as ready to pop up on Mars as on Venus, at an in­stant's no­tice. If it was hid­ing on Mars, it could not pos­si­bly pop up on Venus on an in­stant's no­tice; the fastest it would be al­lowed to move is at the speed of light. Worse, when the elec­tron does pop up on Mars, it must com­mu­ni­cate that fact in­stan­ta­neously to Venus to pre­vent it­self from also pop­ping up there. That re­quires that quan­tum me­chan­ics in­ter­nally com­mu­ni­cates at speeds faster than the speed of light. That is called the Ein­stein-Podol­ski-Rosen para­dox. A fa­mous the­o­rem by John Bell in 1964 im­plies that na­ture re­ally does com­mu­ni­cate in­stan­ta­neously; it is not just some un­known de­fi­ciency in the the­ory of quan­tum me­chan­ics, chap­ter 8.2.

Of course, quan­tum me­chan­ics is largely a mat­ter of in­fer­ence. The wave func­tion can­not be di­rectly ob­served. But that is not as strong an ar­gu­ment against quan­tum me­chan­ics as it may seem. The more you learn about quan­tum me­chan­ics, the more its weird­ness will prob­a­bly be­come in­escapable. Af­ter al­most a cen­tury, quan­tum me­chan­ics is still stand­ing, with no real more rea­son­able com­peti­tors, ones that stay closer to the com­mon sense pic­ture. And the best minds in physics have tried.

From a more prac­ti­cal point of view, you might ob­ject that the Born in­ter­pre­ta­tion cheats: it only ex­plains what the ab­solute value of the wave func­tion is, not what the wave func­tion it­self is. And you would have a very good point there. Ahem. The wave func­tion $\Psi({\skew0\vec r},t)$ it­self gives the “quan­tum am­pli­tude” that the par­ti­cle can be found at po­si­tion ${\skew0\vec r}$. No, in­deed that does not help at all. That is just a de­f­i­n­i­tion.

How­ever, for un­known rea­sons na­ture al­ways com­putes with a wave func­tion, never with prob­a­bil­i­ties. The clas­si­cal ex­am­ple is where you shoot elec­trons at ran­dom at a tiny pin­hole in a wall. Open up a sec­ond hole, and you would ex­pect that every point be­hind the wall would re­ceive more elec­trons, with an­other hole open. The prob­a­bil­ity of get­ting the elec­tron from the sec­ond hole should add to the prob­a­bil­ity of get­ting it from the first one. But that is not what hap­pens. Some points may now get no elec­trons at all. The wave func­tion trace pass­ing through the sec­ond hole may ar­rive with the op­po­site sign of the wave func­tion trace pass­ing through the first hole. If that hap­pens, the net wave func­tion be­comes zero, and so its square mag­ni­tude, the prob­a­bil­ity of find­ing an elec­tron, does too. Elec­trons are pre­vented from reach­ing the lo­ca­tion by giv­ing them an ad­di­tional way to get there. It is weird. Then again, there is lit­tle profit in wor­ry­ing about it.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Ac­cord­ing to quan­tum me­chan­ics, par­ti­cles do not have pre­cise val­ues of po­si­tion or ve­loc­ity when ex­am­ined closely enough.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

What they do have is a “wave func­tion“ that de­pends on po­si­tion.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Larger val­ues of the mag­ni­tude of the wave func­tion, (in­di­cated in this book by darker re­gions,) cor­re­spond to re­gions where the par­ti­cle is more likely to be found if a lo­ca­tion mea­sure­ment is done.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Such a mea­sure­ment changes the wave func­tion; the mea­sure­ment it­self cre­ates the re­duced un­cer­tainty in po­si­tion that ex­ists im­me­di­ately af­ter the mea­sure­ment.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

In other words, the wave func­tion is all there is; you can­not iden­tify a hid­den po­si­tion in a given wave func­tion, just cre­ate a new wave func­tion that more pre­cisely lo­cates the par­ti­cle.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The cre­ation of such a more lo­cal­ized wave func­tion dur­ing a po­si­tion mea­sure­ment is gov­erned by laws of chance: the more lo­cal­ized wave func­tion is more likely to end up in re­gions where the ini­tial wave func­tion had a larger mag­ni­tude.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Proper wave func­tions are nor­mal­ized.