| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
D.36 Photon wave function derivations
The rules of engagement are as follows:
- The Cartesian axes are numbered using an index
 , with
, with

 1, 2, and 3 for
1, 2, and 3 for  ,
,  , and
, and  respectively.
respectively.
- Also,
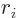 indicates the coordinate in the
indicates the coordinate in the  direction,
direction,
 ,
,  , or
, or  .
.
- Derivatives with respect to a coordinate
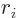 are indicated by
a simple subscript
are indicated by
a simple subscript  .
.
- If the quantity being differentiated is a vector, a comma is
used to separate the vector index from differentiation ones.
- Index
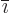 is the number immediately following
is the number immediately following  in the
cyclic sequence ...123123...and
in the
cyclic sequence ...123123...and 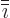 is the number
immediately preceding
is the number
immediately preceding  .
.
- Time derivatives are indicated by a subscript t.
- A bare
 integral sign is assumed to be an integration over
all space, or over the entire box for particles in a box. The
integral sign is assumed to be an integration over
all space, or over the entire box for particles in a box. The
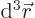 is normally omitted for brevity and to be understood.
is normally omitted for brevity and to be understood.
- A superscript
 indicates a complex conjugate.
indicates a complex conjugate.
D.36.1 Rewriting the energy integral
As given in the text, the energy in an electromagnetic field in free
space that satisfies the Coulomb-Lorenz gauge is, writing out the
square magnitudes and individual components,
However, a bit more general expression is desirable. If only the
Lorenz condition is satisfied, there may also be an electrostatic
potential 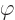 . In that case, a more general expression
for the energy is:
The minus sign for the
. In that case, a more general expression
for the energy is:
The minus sign for the 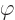 terms appears because this is really
a dot product of relativistic four-vectors. The zeroth components in
such a dot product acquire a minus sign, chapter 1.2.4
and 1.3.2. In derivation {D.32} it was
shown that each of the four integrals is constant. That is because
each component satisfies the Klein-Gordon equation. So their sum is
constant too.
terms appears because this is really
a dot product of relativistic four-vectors. The zeroth components in
such a dot product acquire a minus sign, chapter 1.2.4
and 1.3.2. In derivation {D.32} it was
shown that each of the four integrals is constant. That is because
each component satisfies the Klein-Gordon equation. So their sum is
constant too.
The claim to verify now is that the same energy can be obtained
from integrating the electric and magnetic fields as
Since 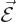

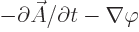 and
and 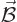


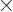
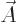 :
:
From now on, it will be understood that there is a summation over  and
and  and that everything has a
and that everything has a 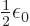 .
Therefore these will no longer be shown.
.
Therefore these will no longer be shown.
Start with the electric field integral. It is, using the above expressions
and multiplying out,
The first term already gives the vector-potential time derivatives in
(1). That leaves the final three terms. Perform an integration by
parts on the first two. It will always be assumed that the potentials
vanish at infinity or that the system is in a periodic box. In that
case there are no boundary terms in an integration by parts. So the
three terms become
However, the divergence  is according to the Lorenz condition
equal to
is according to the Lorenz condition
equal to 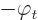

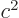 , so
, so
Using the Klein-Gordon equation, 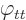

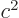

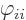 , and then another integration by parts on the
first two terms and renotating
, and then another integration by parts on the
first two terms and renotating  by
by  gives the
gives the
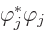 terms in (1).
terms in (1).
Now consider the integral of 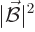 in (2). You get, multiplying out,
in (2). You get, multiplying out,
Now the first and last terms in the right hand side summed over  produce all terms
produce all terms 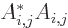 in (1) in which
in (1) in which  and
and  are
different. That leaves the middle terms. An integration by parts
yields
are
different. That leaves the middle terms. An integration by parts
yields
Renotate the indices cyclically to get
(If you want, you can check that this is the same by writing out all
three terms in the sum.) This is equivalent to
as you can see from differentiating and multiplying out. The final
term gives after integration by parts the 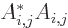 terms in
(1) in which
terms in
(1) in which  and
and  are equal. That leaves the first part. The
term in parentheses is the divergence
are equal. That leaves the first part. The
term in parentheses is the divergence 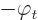

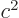 , so the
first part is
, so the
first part is
Perform an integration by parts
Recognizing once more the divergence, this gives the final
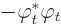

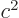 term in (1)
term in (1)
D.36.2 Angular momentum states
The rules of engagement listed at the start of this section apply.
In addition:
- The quantum numbers
 and
and 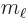 will be renotated by
will be renotated by  and
and  , while
, while 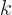 stays
stays 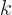 . That is easier to type.
. That is easier to type.
- The quantum numbers are not shown unless needed. For example,
 stands for
stands for 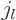 .
.
- A bar on a quantity, like in
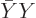 , means the complex
conjugate. In addition, the (unlisted) quantum numbers of spherical
harmonic
, means the complex
conjugate. In addition, the (unlisted) quantum numbers of spherical
harmonic 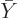 may in general be different from those of
may in general be different from those of 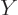 and
are indicated by bars too.
and
are indicated by bars too.
- The symbols
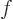 and
and 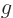 are used as generic scalar functions.
They often stand in particular for the
are used as generic scalar functions.
They often stand in particular for the 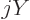 scalar modes.
scalar modes.
- An integral in spherical coordinates takes the form
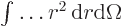 where
where 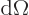

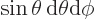 .
.
D.36.2.1 About the scalar modes
The scalar modes are the 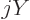 .
.
It will be assumed that the  are zero at the large radius
are zero at the large radius
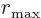 at which the domain is assumed to terminate. That
makes the scalar modes a complete set; any scalar function
at which the domain is assumed to terminate. That
makes the scalar modes a complete set; any scalar function 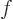 can be written as a combination of them. (That is because they are
the eigenfunctions of the Laplacian inside the sphere, and the zero
boundary condition on the sphere surface
can be written as a combination of them. (That is because they are
the eigenfunctions of the Laplacian inside the sphere, and the zero
boundary condition on the sphere surface 

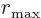 makes the
Laplacian Hermitian. This will not be explicitly proved since it is
very standard.)
makes the
Laplacian Hermitian. This will not be explicitly proved since it is
very standard.)
The Bessel function  of the scalar modes satisfy the ordinary
differential equation, {A.6}
of the scalar modes satisfy the ordinary
differential equation, {A.6}
The following integral is needed (note that  is real):
This is valid for large
is real):
This is valid for large 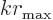 , which applies since
, which applies since
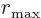 is large and the
is large and the 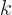 values of interest are finite.
The above result comes from the integral of the square two-dimensional
Bessel functions
values of interest are finite.
The above result comes from the integral of the square two-dimensional
Bessel functions 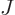 , and a recurrence relation,
[41, 27.18,88], using
, and a recurrence relation,
[41, 27.18,88], using 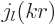

 ,
[1, p 437, 10.1.1], and the asymptotic behavior
of the Bessel function you get from {A.6}
(A.19). To get the leading asymptotic term, each time you
have to differentiate the trigonometric function. And where the
trigonometric function in
,
[1, p 437, 10.1.1], and the asymptotic behavior
of the Bessel function you get from {A.6}
(A.19). To get the leading asymptotic term, each time you
have to differentiate the trigonometric function. And where the
trigonometric function in 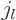 is zero at
is zero at 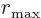 because of
the boundary condition, the one in
because of
the boundary condition, the one in 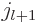 has magnitude 1.
has magnitude 1.
The spherical harmonics are orthonormal on the unit sphere,
{D.14.4}
In other words, the integral is only 1 if 

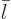 and
and 

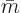 and otherwise it is zero. Further
and otherwise it is zero. Further
D.36.2.2 Basic observations and eigenvalue problem
For any function 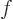
This follows from writing out the right hand side
the latter since 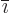 and
and 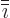 are different indices.
are different indices.
The electric modes
are solenoidal because 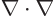
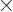
 gives zero. The magnetic modes
gives zero. The magnetic modes
are solenoidal for the same reason, after noting (7) above.
The Laplacian commutes with the operators in front of the scalar
functions in the electric and magnetic modes. That can be seen for
the magnetic ones from
and the final two terms cancel. And the Laplacian also commutes with
the additional 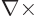 in the electric modes since
differentiations commute.
in the electric modes since
differentiations commute.
From this it follows that the energy eigenvalue problem is satisfied
because by definition of the scalar modes 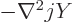

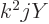 . In addition,
. In addition,
because 
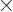
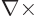


 for a
solenoidal function, (D.1).
for a
solenoidal function, (D.1).
D.36.2.3 Spherical form and net angular momentum
In spherical coordinates, the magnetic mode is
and then the electric mode is
from [41, 20.74,76,82] and for the  component of
component of
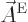 the eigenvalue problem of chapter 4.2.3.
the eigenvalue problem of chapter 4.2.3.
Now note that the 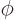 dependence of
dependence of 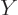 is through a simple factor
is through a simple factor
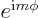 , chapter 4.2.3. Therefore it is seen
that if the coordinate system is rotated over an angle
, chapter 4.2.3. Therefore it is seen
that if the coordinate system is rotated over an angle 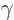 around
the
around
the  -axis, it produces a factor
-axis, it produces a factor  in the vectors.
First of all that means that the azimuthal quantum number of net
angular momentum is
in the vectors.
First of all that means that the azimuthal quantum number of net
angular momentum is  , {A.19}. But it also
means that, {A.19},
, {A.19}. But it also
means that, {A.19},
because either way the vector gets multiplied by 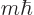 for the
modes. And if it is true for all the modes, then it is true for any
function
for the
modes. And if it is true for all the modes, then it is true for any
function 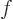 . Since the
. Since the  -axis is not special for general
-axis is not special for general
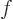 , the same must hold for the
, the same must hold for the  and
and  angular momentum
operators. From that it follows that the modes are also
eigenfunctions of net square angular momentum, with azimuthal quantum
number
angular momentum
operators. From that it follows that the modes are also
eigenfunctions of net square angular momentum, with azimuthal quantum
number  .
.
At the cut-off 

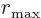 ,
, 
 0, which
gives:
0, which
gives:
Also needed is, differentiating (10):
which used (3) to get rid of the second order derivative of  .
.
D.36.2.4 Orthogonality and normalization
Whether the modes are orthogonal, and whether the Laplacian is
Hermitian, is not obvious because of the weird boundary conditions at
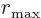 .
.
In general the important relations here
where 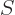 is the surface of the sphere
is the surface of the sphere 

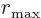 .
The second last line can be verified by differentiating out and the
last line is the divergence theorem.
.
The second last line can be verified by differentiating out and the
last line is the divergence theorem.
The first and second line in (13) show that the Laplacian is Hermitian
if all unequal modes are orthogonal (or have equal 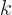 values, but
orthogonality should be shown anyway.). For unequal
values, but
orthogonality should be shown anyway.). For unequal 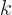 values
orthogonality may be shown by showing that the final surface integral
is zero.
values
orthogonality may be shown by showing that the final surface integral
is zero.
It is convenient to show right away that the electric and magnetic
modes are always mutually orthogonal:
The first two terms in the right hand side can be integrated in the
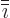 , respectively
, respectively 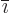 direction and are then zero because
direction and are then zero because
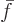 is zero on the spherical surface
is zero on the spherical surface 

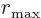 . The final two terms summed over
. The final two terms summed over  can be
renotated by shifting the summation index one unit down, respectively
up in the cyclic sequence to give
can be
renotated by shifting the summation index one unit down, respectively
up in the cyclic sequence to give
the latter because of the form of 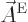 , the fact that
, the fact that

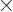
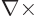


 for a solenoidal
vector, and the energy eigenvalue problem established for
for a solenoidal
vector, and the energy eigenvalue problem established for
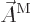 . The final term is zero because
. The final term is zero because
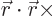 is.
is.
Next consider the orthogonality of the magnetic modes for different
quantum numbers. For 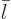
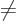
 or
or 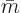
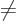
 , the orthogonality follows from (9) and (6). For
, the orthogonality follows from (9) and (6). For 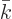
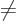
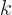 , the orthogonality follows from the final line in (13)
since the magnetic modes are zero at
, the orthogonality follows from the final line in (13)
since the magnetic modes are zero at 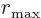 , (11).
, (11).
Finally the electric modes. For 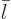
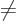
 or
or 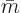
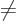
 , the orthogonality follows from (10), (5), and (6).
For
, the orthogonality follows from (10), (5), and (6).
For 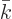
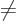
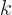 , the orthogonality follows from the
final line in (13). To see that, recognize that
, the orthogonality follows from the
final line in (13). To see that, recognize that
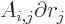

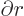 is the radial derivative of
is the radial derivative of
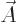 ; therefore using (11) and (12), the integrand vanishes.
; therefore using (11) and (12), the integrand vanishes.
The integral of the absolute square integral of a magnetic mode is,
using (9), (6), and (4),
The integral of the absolute square integral of an electric mode is,
using (10), (5), and (6),
Apply an integration by parts on the second integral,
and then use (3) to get
The normalizations given in the text follow.
D.36.2.5 Completeness
Because of the condition 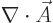
 0, you would generally
speaking expect two different types of modes described by scalar
functions. The electric and magnetic modes seem to fit that bill.
But that does not mean that there could not be say a few more special
modes. What is needed is to show completeness. That means to show
that any smooth vector field satisfying
0, you would generally
speaking expect two different types of modes described by scalar
functions. The electric and magnetic modes seem to fit that bill.
But that does not mean that there could not be say a few more special
modes. What is needed is to show completeness. That means to show
that any smooth vector field satisfying 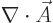
 0 can
be written as a sum of the electric and magnetic modes, and nothing
else.
0 can
be written as a sum of the electric and magnetic modes, and nothing
else.
This author does not know any simple way to do that. It would be
automatic without the solenoidal condition; you would just take each
Cartesian component to be a combination of the scalar modes 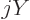 satisfying a zero boundary condition at
satisfying a zero boundary condition at 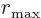 . Then
completeness would follow from the fact that they are eigenfunctions
of the Hermitian Laplacian. Or from more rigorous arguments that you
can find in mathematical books on partial differential equations. But
how to do something similar here is not obvious, at least not to this
author.
. Then
completeness would follow from the fact that they are eigenfunctions
of the Hermitian Laplacian. Or from more rigorous arguments that you
can find in mathematical books on partial differential equations. But
how to do something similar here is not obvious, at least not to this
author.
What will be done is show that any reasonable solenoidal vector can be
written in the form
where 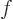 and
and 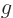 are scalar functions. Completeness then follows
since the modes
are scalar functions. Completeness then follows
since the modes 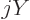 provide a complete description of any arbitrary
function
provide a complete description of any arbitrary
function 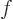 and
and 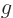 .
.
But to show the above does not seem easy either, so what will be
actually shown is that any vector without radial component can be
written in the form
That is sufficient because the Fourier transform of 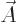 does not
have a radial component, so it will be of this form. And the inverse
Fourier transform of
does not
have a radial component, so it will be of this form. And the inverse
Fourier transform of  is of the form
is of the form 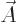 , compare any
book on Fourier transforms and (7).
, compare any
book on Fourier transforms and (7).
The proof that  must be of the stated form is by
construction. Note that automatically, the radial component of the
two terms is zero. Writing out the gradients in spherical
coordinates, [41, 20.74,82], multiplying out the cross
products and equating components gives at any arbitrary radius
must be of the stated form is by
construction. Note that automatically, the radial component of the
two terms is zero. Writing out the gradients in spherical
coordinates, [41, 20.74,82], multiplying out the cross
products and equating components gives at any arbitrary radius 
Now decompose this in Fourier modes 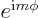 in the
in the 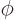 direction:
direction:
For 
 0,
0, 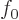 and
and 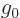 follow by integration. Note that the
integrands are periodic of period
follow by integration. Note that the
integrands are periodic of period 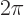 and antisymmetric about the
and antisymmetric about the
 -axis. That makes
-axis. That makes 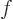 and
and 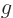 periodic of period
periodic of period 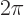 too,
too,
For 
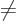 0 make a coordinate transform from
0 make a coordinate transform from 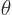 to
to
Note that 
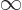
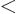
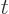
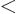
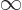 . If anybody is
actually reading this, send me an email. The system becomes after
cleaning up
. If anybody is
actually reading this, send me an email. The system becomes after
cleaning up
It is now easiest to solve the above equations for each of the two
right hand sides separately. Here the first right hand side will be
done, the second right hand side goes similarly.
From the two equations it is seen that 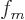 must satisfy
must satisfy
and 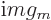 must the derivative of
must the derivative of 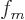 . The solution
satisfying the required regularity at
. The solution
satisfying the required regularity at  is,
[41, 19.8],
is,
[41, 19.8],
That finishes the construction, but you may wonder about potential
nonexponential terms in the first integral at 
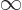 and the second
integral at
and the second
integral at 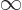 . Those would produce weak logarithmic
singularities in the physical
. Those would produce weak logarithmic
singularities in the physical 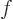 and
and 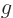 . You could simply
guess that the two right hand sides will combine so that these terms
drop out. After all, there is nothing special about the chosen
direction of the
. You could simply
guess that the two right hand sides will combine so that these terms
drop out. After all, there is nothing special about the chosen
direction of the  -axis. If you choose a different axis, it will
show no singularities at the old
-axis. If you choose a different axis, it will
show no singularities at the old  -axis, and the solution is unique.
-axis, and the solution is unique.
For more confidence, you can check the cancellation explicitly for the
leading order, 
 1 terms. But there is a better way. If the right
hand sides are zero within a nonzero angular distance
1 terms. But there is a better way. If the right
hand sides are zero within a nonzero angular distance 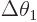 from the
from the  -axis, there are no singularities. And it is easy to
split off a part of
-axis, there are no singularities. And it is easy to
split off a part of  that is zero within
that is zero within 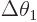 of
the axis and then changes smoothly to the correct
of
the axis and then changes smoothly to the correct  in an
angular range from
in an
angular range from 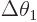 to
to 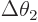 from the axis.
The remainder of
from the axis.
The remainder of  can than be handled by using say the
can than be handled by using say the
 -axis as the axis of the spherical coordinate system.
-axis as the axis of the spherical coordinate system.
D.36.2.6 Density of states
The spherical Bessel function is for large arguments proportional to


 or
or 

 . Either way, the zeros are
spaced
. Either way, the zeros are
spaced 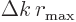

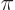 apart. So there is one
state
apart. So there is one
state 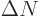
 1 in an interval
1 in an interval 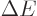

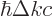



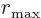 . The ratio
gives the stated density of states.
. The ratio
gives the stated density of states.
D.36.2.7 Parity
Parity is what happens to the sign of the wave function under a parity
transformation. A parity transformation inverts the positive
direction of all three Cartesian axes, replacing any position vector
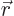 by
by 
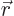 . The parity of something is 1 or even if it
does not change, and
. The parity of something is 1 or even if it
does not change, and  1 or odd if it changes sign. Under a parity
transformation, the operators
1 or odd if it changes sign. Under a parity
transformation, the operators 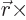 and
and 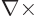 flip over
the parity of what they act on. On the other hand,
flip over
the parity of what they act on. On the other hand,
 has the same parity as
has the same parity as 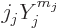 ;
the spatial components flip over, but so do the unit vectors that
multiply them. And the parity of
;
the spatial components flip over, but so do the unit vectors that
multiply them. And the parity of 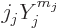 is even if
is even if  is
even and odd if
is
even and odd if  is odd. The stated parities follow.
is odd. The stated parities follow.
D.36.2.8 Orbital angular momentum of the states
In principle a state of definite net angular momentum  and definite
spin 1 may involve orbital angular momentum
and definite
spin 1 may involve orbital angular momentum 

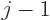 ,
, 

 and
and 

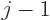 , chapter 7.4.2. But
states of definite parity restrict that to either only odd values or
only even values, {A.20}. To get the stated parities,
, chapter 7.4.2. But
states of definite parity restrict that to either only odd values or
only even values, {A.20}. To get the stated parities,


 for magnetic states and
for magnetic states and 

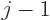 or
or 

 for electric ones.
for electric ones.
woof.
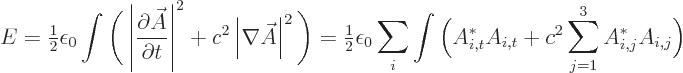
![$\parbox{400pt}{\hfill$\displaystyle
E = {\textstyle\frac{1}{2}}\epsilon_0 \big...
...hi_t^* \varphi_t
+ \sum_{j=1}^3 \varphi_j^* \varphi_j\bigg)\bigg]
$\hfill(1)}$](img6474.gif)
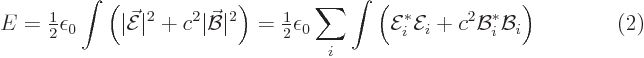
![]()
![]()
![]() .
.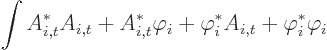
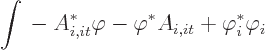
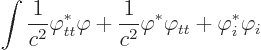
![]()
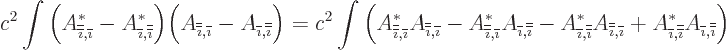
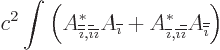
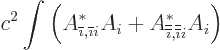
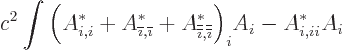
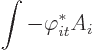
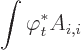
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()


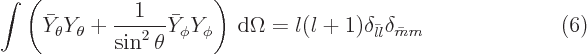
![]()
![]()
![]()
![]() .
.![$\parbox{400pt}{\hspace{11pt}\hfill$\displaystyle
\skew3\vec A^{\rm M} = {\skew...
...Y_\theta - {\hat\imath}_\theta
\frac{1}{\sin\theta} Y_\phi\right]
$\hfill(9)}$](img6521.gif)
![$\parbox{400pt}{\hspace{15pt}\hfill$\displaystyle
\skew3\vec A^{\rm E} = \nabla...
... Y_\theta + {\hat\imath}_\phi
\frac{1}{\sin\theta} Y_\phi\right]
$\hfill(10)}$](img6522.gif)
![]()
![]()
![]() ,
,![]()
![]() -
-![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![$\parbox{400pt}{\hspace{11pt}\hfill$\displaystyle
\mbox{At $r_{\rm{max}}$:} \qq...
... Y_\theta + {\hat\imath}_\phi
\frac{1}{\sin\theta} Y_\phi\right]
$\hfill(11)}$](img6525.gif)
![$\parbox{400pt}{\hspace{11pt}\hfill$\displaystyle
\mbox{At $r_{\rm{max}}$:} \qq...
... Y_\theta + {\hat\imath}_\phi
\frac{1}{\sin\theta} Y_\phi\right]
$\hfill(12)}$](img6526.gif)
![]() .
.
![]()
![]()
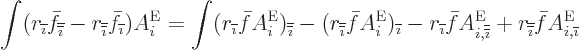
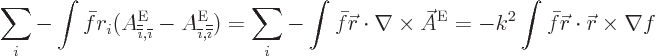
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ;
;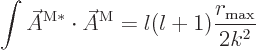
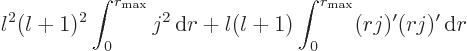
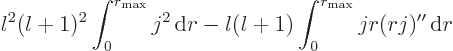
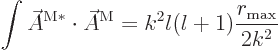
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
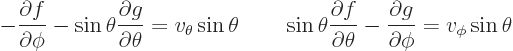
![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
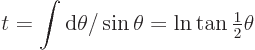
![]()
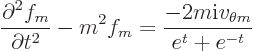
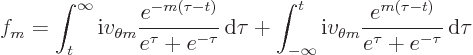
![]()
![]()
![]() .
.![]()
![]() .
.![]() -
-![]() -
-![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]() 1
1![]()
![]()
![]()
![]() ;
;![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()