| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.20 Angular momentum of vector particles
This addendum is concerned with vector particles, particles whose wave
functions are vectors. To be sure, the wave function of an electron
can also be written as a vector, chapters 3.1 and
5.5.1:
But that is not a normal vector. It is a two-dimensional vector in
three-dimensional space, and is known as a spinor. This addendum is
concerned with wave functions that are normal three-dimensional
vectors. That is of importance for understanding, for example, the
spin angular momentum of photons. A photon is a vector particle,
though a special one. It will be shown in this addendum that the spin
of a vector particle is 1. The parity of such a particle will also be
discussed.
To really appreciate this addendum, you may want to read the previous
addendum {A.19} first. In any case, according to
that addendum angular momentum is related to what happens to the wave
function under rotation of the coordinate system. In particular, the
angular momentum in the  -direction is related to what happens if
the coordinate system is rotated around the
-direction is related to what happens if
the coordinate system is rotated around the  -axis.
-axis.
Consider first the simplest possible vector wave function:
Here 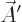 is a constant vector. Also
is a constant vector. Also 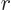 is the distance from the
origin around which the angular momentum is defined. Finally,
is the distance from the
origin around which the angular momentum is defined. Finally, 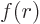 is any arbitrary function of
is any arbitrary function of 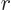 . The big question is now what
happens to this wave function if the coordinate system is rotated over
some angle
. The big question is now what
happens to this wave function if the coordinate system is rotated over
some angle 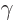 around the
around the  -axis.
-axis.
Figure A.8:
Effect
of rotation of the coordinate system on a vector. The vector is
physically the same, but it has a different mathematical
representation, different components, in the two coordinate
systems.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(300,15...
...}
\put(-102,32.5){\makebox(0,0)[r]{${\hat\jmath}$}}
\end{picture}
\end{figure}](img4276.gif) |
The factor 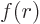 does not change under rotations because the distance
from the origin does not. But the vector
does not change under rotations because the distance
from the origin does not. But the vector 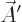 does
change. Figure A.8 shows what happens. The vector in the
rotated coordinate system
does
change. Figure A.8 shows what happens. The vector in the
rotated coordinate system 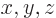 has components
has components
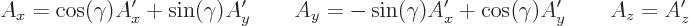 |
(A.82) |
For example, the first relation expresses that 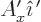 has a
component
has a
component 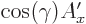 in the direction of
in the direction of 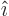 , while
, while
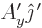 has a component
has a component 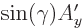 in that direction.
The second expression follows similarly. The
in that direction.
The second expression follows similarly. The  -component does not
change under the rotation.
-component does not
change under the rotation.
Now consider three very special vectors:
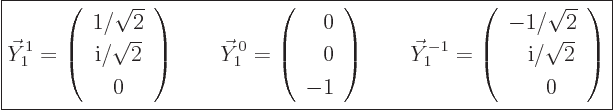 |
(A.83) |
If you plug 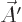

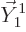 into the relations
(A.82) given above and use the Euler identity
(2.5), you get
into the relations
(A.82) given above and use the Euler identity
(2.5), you get 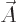

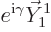 . So the vector
. So the vector 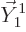 changes
by a mere scalar factor, the exponential
changes
by a mere scalar factor, the exponential 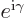 , under
the rotation of the coordinate system. According to the relationship
between rotations and angular momentum, {A.19}, that
makes
, under
the rotation of the coordinate system. According to the relationship
between rotations and angular momentum, {A.19}, that
makes 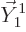 a state of definite angular momentum in the
a state of definite angular momentum in the
 -direction. Also, the magnetic quantum number
-direction. Also, the magnetic quantum number 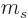 of the
momentum in the
of the
momentum in the  -direction is by definition the coefficient of
-direction is by definition the coefficient of
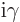 in the exponential factor
in the exponential factor 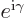

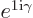 . Here that is 1, so
. Here that is 1, so 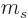
 1. This value
is shown as the superscript of the state
1. This value
is shown as the superscript of the state 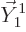 . The
actual angular momentum in the
. The
actual angular momentum in the  -direction is
-direction is 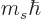 , so
it is
, so
it is 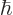 for this state. This angular momentum should be called
spin, in analogy to the case for the electron. It is due to the fact
that the wave function is a vector.
for this state. This angular momentum should be called
spin, in analogy to the case for the electron. It is due to the fact
that the wave function is a vector.
The vector 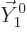 has only a
has only a  -component, so it does not
change under the rotation. Phrased differently, it changes by a unit
factor
-component, so it does not
change under the rotation. Phrased differently, it changes by a unit
factor 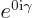 . That makes its magnetic quantum number
. That makes its magnetic quantum number
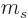 zero, as the superscript in
zero, as the superscript in 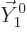 says. Then the
angular momentum in the
says. Then the
angular momentum in the  -direction of this state is zero too.
Finally, the vector
-direction of this state is zero too.
Finally, the vector 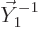 changes by a factor
changes by a factor
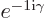 under rotation, so it has
under rotation, so it has 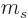

 1, as its
superscript says, and the angular momentum in the
1, as its
superscript says, and the angular momentum in the  -direction is
-direction is

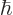 .
.
To get at square angular momentum, first the operator 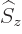 of spin
angular momentum around the
of spin
angular momentum around the  -axis is needed. The relation between
angular momentum and rotations shows that this operator takes the
general form, {A.19} (A.76),
-axis is needed. The relation between
angular momentum and rotations shows that this operator takes the
general form, {A.19} (A.76),
Here 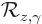 is the operator that describes the effect of the
rotation of the coordinate system on the wave function. Applied on
the vector
is the operator that describes the effect of the
rotation of the coordinate system on the wave function. Applied on
the vector 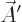 in the unrotated coordinate system, that means
in the unrotated coordinate system, that means
Plugging in the components of 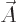 as given earlier,
(A.82), and taking the limits using l’Hôpital, that
produces
as given earlier,
(A.82), and taking the limits using l’Hôpital, that
produces
So the operator 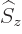 drops the
drops the  -component and swaps the other
two components, changing the sign of the first, and then adds a factor
-component and swaps the other
two components, changing the sign of the first, and then adds a factor
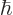
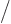
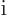 . If the same operations are performed another
time, the net result is:
. If the same operations are performed another
time, the net result is:
So the square operator just drops the  -component and adds a factor
-component and adds a factor
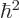 .
.
Of course, the operators 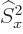 and
and 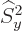 are defined
similarly. There is nothing special about the
are defined
similarly. There is nothing special about the  -axis. The operator
of square spin angular momentum is defined as
-axis. The operator
of square spin angular momentum is defined as
Since each of the operators in the right hand side drops a different
component and adds a factor 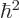 to the other two, the total for
any vector
to the other two, the total for
any vector 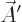 is,
is,
So the square spin operator always produces a simple multiple of the
original vector. That makes any vector an eigenvector of
square spin angular momentum. Also, the azimuthal quantum number
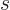 , the spin, can by definition be found from equating the
coefficient
, the spin, can by definition be found from equating the
coefficient 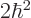 of
of 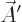 in the right hand side above to
in the right hand side above to
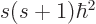 . The only nonnegative value
. The only nonnegative value 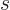 that can
satisfy this condition is
that can
satisfy this condition is 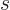
 1.
1.
That then means that the spin 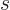 of vector particles is equal to 1.
So a vector particle is a boson of spin 1. The subscript on the
special vectors
of vector particles is equal to 1.
So a vector particle is a boson of spin 1. The subscript on the
special vectors 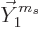 indicates their spin
indicates their spin 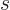
 1.
1.
You can write the most general vector wave function in the form
Then you can put the coefficients in a vector much like the wave function
of the electron, but now three-dimensional:
Like the electron, the vector particle can of course also have orbital
angular momentum. That is due to the coefficients 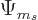 in the
wave function above. So far it has been assumed that these
coefficients only depended on the distance
in the
wave function above. So far it has been assumed that these
coefficients only depended on the distance 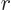 from the origin.
However, consider the following more general component of a vector
wave function:
from the origin.
However, consider the following more general component of a vector
wave function:
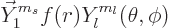 |
(A.84) |
Here 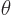 and
and 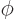 are the position angles in spherical
coordinates, and
are the position angles in spherical
coordinates, and 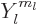 is a so-called spherical harmonic
of orbital angular momentum, chapter 4.2.3. For the
above wave function to be properly normalized,
is a so-called spherical harmonic
of orbital angular momentum, chapter 4.2.3. For the
above wave function to be properly normalized,
(To check this, take a dot, or rather inner, product of the wave
function with itself. Then integrate over all space using spherical
coordinates and the orthonormality of the spherical harmonics.)
The wave function (A.84) above has orbital angular momentum
in the  -direction equal to
-direction equal to 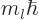 in addition to the spin
angular momentum
in addition to the spin
angular momentum 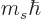 . So the total angular momentum in
the
. So the total angular momentum in
the  -direction is
-direction is 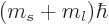 . To check that,
note that under rotations of the coordinate system, the vector changes
by a factor
. To check that,
note that under rotations of the coordinate system, the vector changes
by a factor 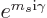 while the spherical harmonic changes by
an additional factor
while the spherical harmonic changes by
an additional factor 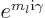 . That makes the total
change a factor
. That makes the total
change a factor 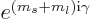 .
.
In general, then, the magnetic quantum number 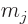 of the net
angular momentum is simply the sum of the spin and orbital ones,
of the net
angular momentum is simply the sum of the spin and orbital ones,
 |
(A.85) |
However, the situation for the azimuthal quantum number  of the net
angular momentum is not so simple. In general the wave function
(A.84) above will have uncertainty in the value of
of the net
angular momentum is not so simple. In general the wave function
(A.84) above will have uncertainty in the value of
 . Combinations of wave functions of the form
(A.84) are usually needed to get states of definite
. Combinations of wave functions of the form
(A.84) are usually needed to get states of definite
 .
.
That is a complicated issue best left to chapter 12.
But a couple of special cases are worth mentioning already. First, if
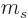
 1 and
1 and 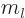

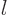 , or alternatively, if
, or alternatively, if 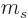

 1 and
1 and 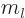


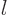 , then
, then  is simply the sum of
the spin and orbital azimuthal quantum numbers
is simply the sum of
the spin and orbital azimuthal quantum numbers 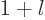 .
.
The other special case is that there is zero net angular momentum.
Zero net angular momentum means that the wave function is exactly the
same regardless how the coordinate system is rotated. And that only
happens for a vector wave function if it is purely radial:
Here 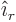 is the unit vector sticking radially outward away from
the origin. The final constant is the spherical harmonic
is the unit vector sticking radially outward away from
the origin. The final constant is the spherical harmonic
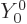 . It is needed the satisfy the normalization requirement
unless you change the one on
. It is needed the satisfy the normalization requirement
unless you change the one on  .
.
The above state has zero net angular momentum. The question of
interest is what can be said about its spin and orbital angular
momentum. To answer that, it must be rewritten in terms of Cartesian
components. Now the unit vector 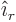 has Cartesian components
has Cartesian components
The spatial factors in this expression can be written in terms of the
spherical harmonics 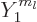 , chapter 4.2.3. That
gives the state of zero net angular momentum as
, chapter 4.2.3. That
gives the state of zero net angular momentum as
To check this, just plug in the expressions for the 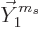 of (A.83), and for the
of (A.83), and for the 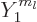 of table 4.3.
of table 4.3.
The bottom line is that by combining states of unit spin 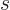
 1,
and unit orbital angular momentum
1,
and unit orbital angular momentum 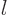
 1, you can create a state
of zero net angular momentum,
1, you can create a state
of zero net angular momentum, 
 0. Note also that in each of
the three terms in the right hand side above,
0. Note also that in each of
the three terms in the right hand side above, 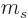 and
and 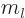 add up
to zero. A state of zero angular momentum
add up
to zero. A state of zero angular momentum 
 0 must have
0 must have 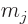
 0 without uncertainty. Further note that the values of both the
spin and orbital angular momentum in the
0 without uncertainty. Further note that the values of both the
spin and orbital angular momentum in the  -direction are
uncertain. Each of the two has measurable values
-direction are
uncertain. Each of the two has measurable values 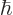 , 0, or
, 0, or

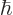 with equal probability
with equal probability 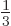 .
.
The above relation may be written more neatly in terms of “ket
notation.” In ket notation, an angular momentum state with
azimuthal quantum number  and magnetic quantum number
and magnetic quantum number 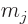 is
indicated as
is
indicated as 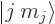 . Using this notation, and dropping
the common factor
. Using this notation, and dropping
the common factor 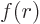 , the above relation can be written as
, the above relation can be written as
Here the subscripts  ,
, 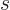 , and
, and 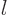 indicate net, spin,
and orbital angular momentum, respectively.
indicate net, spin,
and orbital angular momentum, respectively.
There is a quicker way to get this result than going through the above
algebraic mess. You can simply read off the coefficients in the
appropriate column of the bottom-right tabulation in figure
12.6. (In this figure take 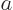 to stand for spin,
to stand for spin, 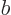 for
orbital, and
for
orbital, and 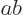 for net angular momentum.) Figure 12.6
also has the coefficients for many other net spin states that you
might need. A derivation of the figure must wait until chapter
12.
for net angular momentum.) Figure 12.6
also has the coefficients for many other net spin states that you
might need. A derivation of the figure must wait until chapter
12.
The parity of vector wave functions is also important. Parity is what
happens to a wave function if you invert the positive direction of all
three Cartesian axes. What happens to a vector wave function under
such an inversion can vary. A normal, or “polar,” vector changes sign when you invert the axes. For
example, a position vector 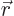 in classical physics is a polar
vector. Each position coordinate
in classical physics is a polar
vector. Each position coordinate  ,
, 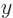 , and
, and  changes sign, and therefore so does the entire vector. Similarly, a
velocity vector
changes sign, and therefore so does the entire vector. Similarly, a
velocity vector  is a polar vector; it is just the time
derivative of position. A particle with a vector wave function that
behaves like a normal vector has negative intrinsic parity. The sign
of the wave function flips over under axes inversion. Particles of
this type turn out to include the photon.
is a polar vector; it is just the time
derivative of position. A particle with a vector wave function that
behaves like a normal vector has negative intrinsic parity. The sign
of the wave function flips over under axes inversion. Particles of
this type turn out to include the photon.
But now consider an example like a classical angular momentum vector,
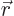

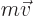 . Since both the position and the
velocity change sign under spatial inversion, a classical angular
momentum vector stays the same. A vector that does not change under
axes inversion is called a “pseudovector” or “axial” vector. A particle whose wave function behaves like a
pseudovector has positive intrinsic parity.
. Since both the position and the
velocity change sign under spatial inversion, a classical angular
momentum vector stays the same. A vector that does not change under
axes inversion is called a “pseudovector” or “axial” vector. A particle whose wave function behaves like a
pseudovector has positive intrinsic parity.
Note however that the orbital angular momentum of the particle also
has an effect on the net parity. In particular, if the quantum number
of orbital angular momentum 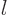 is odd, then the net parity is the
opposite of the intrinsic one. If the quantum number
is odd, then the net parity is the
opposite of the intrinsic one. If the quantum number 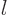 is even,
then the net parity is the intrinsic one. The reason is that
spherical harmonics change sign under spatial inversion if
is even,
then the net parity is the intrinsic one. The reason is that
spherical harmonics change sign under spatial inversion if 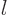 is odd,
but not when
is odd,
but not when 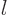 is even, {D.14}.
is even, {D.14}.
Particles of all types often have definite parity. Such a particle
may still have uncertainty in 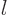 . But if parity is definite,
the measurable values of
. But if parity is definite,
the measurable values of 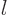 will need to be all even or all odd.
will need to be all even or all odd.
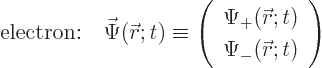
![]() -
-![]() -
-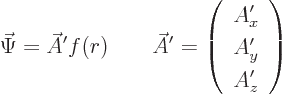
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(300,15...
...}
\put(-102,32.5){\makebox(0,0)[r]{${\hat\jmath}$}}
\end{picture}
\end{figure}](img4276.gif)
![]()
![]()
![]()
![]()
![]() -
-![]() .
.![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]() 1
1![]() -
-![]()
![]() .
.![]()
![]() -
-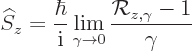
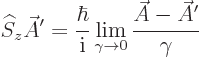
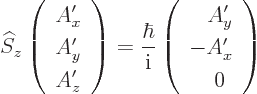
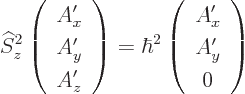
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
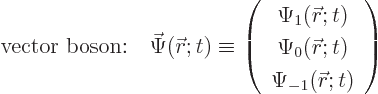
![]()
![]()
![]() -
-![]()
![]() .
.![]() -
-![]() .
.![]()
![]() .
.![]() .
.![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() 1
1![]()
![]()
![]()
![]() ,
,![]()
![]() .
.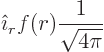
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()