A.23 Quan­ti­za­tion of ra­di­a­tion

Long ago, the elec­tro­mag­netic field was de­scribed in terms of clas­si­cal physics by Maxwell, chap­ter 13. His equa­tions have stood up well to spe­cial rel­a­tiv­ity. How­ever, they need cor­rec­tion for quan­tum me­chan­ics. Ac­cord­ing to the Planck-Ein­stein re­la­tion, the elec­tro­mag­netic field comes in dis­crete par­ti­cles of en­ergy $\hbar\omega$ called pho­tons. A clas­si­cal elec­tro­mag­netic field can­not ex­plain that. This ad­den­dum will de­rive the quan­tum field in empty space. While the de­scrip­tion tries to be rea­son­ably self-con­tained, to re­ally ap­pre­ci­ate the de­tails you may have to read some other ad­denda too. It may also be noted that the dis­cus­sion here is quite dif­fer­ent from what you will find in other sources, {N.12}.

First, rep­re­sent­ing the elec­tro­mag­netic field us­ing the pho­tons of quan­tum me­chan­ics is called “sec­ond quan­ti­za­tion.” No, there is no ear­lier quan­ti­za­tion of the elec­tro­mag­netic field in­volved. The word sec­ond is there for his­tor­i­cal rea­sons. His­tor­i­cally, physi­cists have found it hys­ter­i­cal to con­fuse stu­dents.

In the quan­tum de­scrip­tion, the elec­tro­mag­netic field is an ob­serv­able prop­erty of pho­tons. And the key as­sump­tion of quan­tum me­chan­ics is that ob­serv­able prop­er­ties of par­ti­cles are the eigen­val­ues of Her­mit­ian op­er­a­tors, chap­ter 3. Fur­ther­more, these op­er­a­tors act on wave func­tions that are as­so­ci­ated with the par­ti­cles.

There­fore, sec­ond quan­ti­za­tion is ba­si­cally straight­for­ward. Find the na­ture of the wave func­tion of pho­tons. Then iden­tify the Her­mit­ian op­er­a­tors that give the ob­serv­able elec­tro­mag­netic field.

How­ever, to achieve this in a rea­son­able man­ner re­quires a bit of prepa­ra­tion. To un­der­stand pho­ton wave func­tions, an un­der­stand­ing of a few key con­cepts of clas­si­cal elec­tro­mag­net­ics is es­sen­tial. And the Her­mit­ian op­er­a­tors that act on these wave func­tions are quite dif­fer­ent from the typ­i­cal op­er­a­tors nor­mally used in this book. In par­tic­u­lar, they in­volve op­er­a­tors that cre­ate and an­ni­hi­late pho­tons. Cre­ation and an­ni­hi­la­tion of par­ti­cles is a purely rel­a­tivis­tic ef­fect, de­scribed by so-called quan­tum field the­ory.

Also, af­ter the field has been quan­tized, then of course you want to see what the ef­fects of the quan­ti­za­tion re­ally are, in terms of ob­serv­able quan­ti­ties.

A.23.1 Prop­er­ties of clas­si­cal elec­tro­mag­netic fields

Clas­si­cal elec­tro­mag­net­ics is dis­cussed in con­sid­er­able de­tail in chap­ter 13.2 and 13.3. Here only a few se­lected re­sults are needed.

The clas­si­cal elec­tro­mag­netic field is a com­bi­na­tion of a so-called elec­tric field $\skew3\vec{\cal E}$ and a mag­netic field $\skew2\vec{\cal B}$. These are mea­sures for the forces that the field ex­erts on any charged par­ti­cles in­side the field. The clas­si­cal ex­pres­sion for the force on a charged par­ti­cle is the so-called Lorentz force law

$$q \left(\skew3\vec{\cal E}+ \vec v\times \skew2\vec{\cal B}\right)$$

where $q$ is the charge of the par­ti­cle and $\vec{v}$ its ve­loc­ity. How­ever, this is not re­ally im­por­tant here since quan­tum me­chan­ics uses nei­ther forces nor ve­loc­i­ties.

What is im­por­tant is that elec­tro­mag­netic fields carry en­ergy. That is how the sun heats up the sur­face of the earth. The elec­tro­mag­netic en­ergy in a vol­ume ${\cal V}$ is given by, chap­ter 13.2 (13.11):

$$E_{\cal V}={\textstyle\frac{1}{2}} \epsilon_0 \int_{\cal V... ...E}^2+c^2\skew2\vec{\cal B}^2\right){ \rm d}^3{\skew0\vec r} %$$ (A.152)

where $\epsilon_0$ $\vphantom0\raisebox{1.5pt}{$=$}$ 8.85 10$\POW9,{-12}$ C$\POW9,{2}$/J m is called the per­mit­tiv­ity of space and $c$ $\vphantom0\raisebox{1.5pt}{$=$}$ 3 10$\POW9,{8}$ m/s the speed of light. As you might guess, the en­ergy per unit vol­ume is pro­por­tional to the square fields. Af­ter all, no fields, no en­ergy; also the en­ergy should al­ways be pos­i­tive. The pres­ence of the per­mit­tiv­ity of space is needed to get proper units of en­ergy. The ad­di­tional fac­tor $\frac12$ is not so triv­ial; it is typ­i­cally de­rived from ex­am­in­ing the en­ergy stored in­side con­densers and coils. That sort of de­tail is out­side the scope of this book.

Quan­tum me­chan­ics is in terms of po­ten­tials in­stead of forces. As al­ready noted in chap­ter 1.3.2, in clas­si­cal elec­tro­mag­net­ics there is both a scalar po­ten­tial $\varphi$ as well as a vec­tor po­ten­tial $\skew3\vec A$. In clas­si­cal elec­tro­mag­net­ics these po­ten­tials by them­selves are not re­ally im­por­tant. What is im­por­tant is that their de­riv­a­tives give the fields. Specif­i­cally:

$$\skew3\vec{\cal E}= - \nabla \varphi - \frac{\partial \skew... ...l t} \qquad \skew2\vec{\cal B}= \nabla \times \skew3\vec A %$$ (A.153)

Here the op­er­a­tor

$$\nabla = {\hat\imath}\frac{\partial}{\partial x} + {\hat\j... ...ac{\partial}{\partial y} + {\hat k}\frac{\partial}{\partial z}$$

is called nabla or del. As an ex­am­ple, for the $z$ com­po­nents of the fields:

$${\cal E}_z = - \frac{\partial\varphi}{\partial z} - \frac{\... ...ac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y}$$

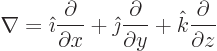
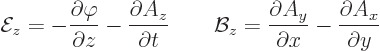
Quan­tum me­chan­ics is all about the po­ten­tials. But the po­ten­tials are not unique. In par­tic­u­lar, for any ar­bi­trary func­tion $\chi$ of po­si­tion and time, you can find two dif­fer­ent po­ten­tials $\varphi'$ and $\skew3\vec A'$ that pro­duce the ex­act same elec­tric and mag­netic fields as $\varphi$ and $\skew3\vec A$. These po­ten­tials are given by

$$\varphi' = \varphi - \frac{\partial\chi}{\partial t} \qquad \skew3\vec A' = \skew3\vec A+ \nabla \chi %$$ (A.154)

(To check that the fields for these po­ten­tials are in­deed the same, note that $\nabla$ $\times$ $\nabla\chi$ is zero for any func­tion $\chi$.) This in­de­ter­mi­nacy in po­ten­tials is the fa­mous gauge prop­erty of the elec­tro­mag­netic field. The ar­bi­trary func­tion $\chi$ is the gauge func­tion.

Clas­si­cal rel­a­tivis­tic me­chan­ics likes to com­bine the four scalar po­ten­tials in a four-di­men­sion­al vec­tor, or four-vec­tor, chap­ter 1.3.2:

$${\buildrel\raisebox{-1.5pt}[0pt][0pt] {\hbox{\hspace{2.5pt}... ...(\begin{array}{c}\varphi/c\ A_x\ A_y\ A_z\end{array}\right)$$

A.23.2 Pho­ton wave func­tions

The wave func­tion of pho­tons was dis­cussed in ad­den­dum {A.21}. A sum­mary of the key re­sults will be given here.

Su­per­fi­cially, the pho­ton wave func­tion ${\buildrel\raisebox{-1.5pt}[0pt][0pt] {\hbox{\hspace{2.5pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over A}_{\kern-1pt\gamma}$ takes the same form as an elec­tro­mag­netic po­ten­tial four-vec­tor like in the pre­vi­ous sub­sec­tion. How­ever, where clas­si­cal po­ten­tials are real, the pho­ton wave func­tion is in gen­eral com­plex. And un­like phys­i­cal po­ten­tials, the de­riv­a­tives of the pho­ton wave func­tion are not phys­i­cally ob­serv­able.

Fur­ther­more, to use the pho­ton wave func­tion in an rea­son­ably ef­fi­cient man­ner, it is es­sen­tial to sim­plify it. The gauge prop­erty of the pre­vi­ous sub­sec­tion im­plies that the wave func­tion is not unique. So among all the pos­si­ble al­ter­na­tives, it is smart to se­lect the sim­plest. And in empty space, as dis­cussed here, the sim­plest pho­ton wave func­tion is of the form:

$${\buildrel\raisebox{-1.5pt}[0pt][0pt] {\hbox{\hspace{2.5pt}... ...d{array}\right) \qquad \nabla \cdot \skew3\vec A_\gamma = 0 %$$

The gauge func­tion cor­re­spond­ing to this wave func­tion is called the Coulomb-Lorenz gauge. Seen from a mov­ing co­or­di­nate sys­tem, this form of the wave func­tion gets messed up, so do not do that.

The real in­ter­est is in quan­tum states of def­i­nite en­ergy. Now for a non­rel­a­tivis­tic par­ti­cle, wave func­tions with def­i­nite en­ergy must be eigen­func­tions of the so-called Hamil­ton­ian eigen­value prob­lem. That eigen­value prob­lem is also known as the time-in­de­pen­dent Schrö­din­ger equa­tion. How­ever, a rel­a­tivis­tic par­ti­cle of zero rest mass like the pho­ton must sat­isfy a dif­fer­ent eigen­value prob­lem, {A.21}:

$$- \nabla^2 \skew3\vec A_\gamma^{\rm {e}} = k^2 \skew3\vec A... ...= \frac{p}{\hbar} \qquad E = \hbar \omega \quad p = \hbar k %$$ (A.155)

Here $\skew3\vec A_\gamma^{\rm {e}}$ is the en­ergy eigen­func­tion. Fur­ther $p$ is the mag­ni­tude of the lin­ear mo­men­tum of the pho­ton. The sec­ond-last equa­tion is the so-called Planck-Ein­stein re­la­tion that gives the pho­ton en­ergy $E$ in terms of its fre­quency $\omega$, while the last equa­tion is the de Broglie re­la­tion that gives the pho­ton mo­men­tum $p$ in terms of its wave num­ber $k$. The re­la­tion be­tween fre­quency and wave num­ber is $\omega$ $\vphantom0\raisebox{1.5pt}{$=$}$ $kc$ with $c$ the speed of light.

The sim­plest en­ergy eigen­func­tions are those that have def­i­nite lin­ear mo­men­tum. A typ­i­cal ex­am­ple of such an en­ergy eigen­func­tion is

$$\skew3\vec A_\gamma^{\rm {e}} = {\hat k}e^{{\rm i}k y}$$ (A.156)

This wave func­tion has def­i­nite lin­ear mo­men­tum ${\hat\jmath}{\hbar}k$, as you can see from ap­ply­ing the com­po­nents of the lin­ear mo­men­tum op­er­a­tor $\hbar\nabla$$\raisebox{.5pt}{$/$}$​${\rm i}$ on it. And it is an en­ergy eigen­func­tion, as you can ver­ify by sub­sti­tu­tion in (A.155). Fur­ther, since the wave func­tion vec­tor is in the $z$-​di­rec­tion, it is called lin­early po­lar­ized in the $z$-​di­rec­tion.

Now the pho­ton wave func­tion ${\buildrel\raisebox{-1.5pt}[0pt][0pt] {\hbox{\hspace{2.5pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over A}_{\kern-1pt\gamma}$ is not a clas­si­cal elec­tro­mag­netic po­ten­tial. The “elec­tric and mag­netic fields” $\skew3\vec{\cal E}_\gamma$ and $\skew2\vec{\cal B}_\gamma$ that you would find by us­ing the clas­si­cal ex­pres­sions (A.153) are not phys­i­cally ob­serv­able quan­ti­ties. So they do not have to obey the clas­si­cal ex­pres­sion (A.152) for the en­ergy in an elec­tro­mag­netic field.

How­ever, you make life a lot sim­pler for your­self if you nor­mal­ize the pho­ton wave func­tions so that they do sat­isfy it. That pro­duces a nor­mal­ized wave func­tion and cor­re­spond­ing un­ob­serv­able fields of the form, {A.21}:

$$\skew3\vec A_\gamma^{\rm n}= \frac{\varepsilon_k}{{\rm i}kc... ...ilon_k}{{\rm i}k} \nabla\times\skew3\vec A_\gamma^{\rm {e}} %$$ (A.157)

where the con­stant $\varepsilon_k$ is found by sub­sti­tu­tion into the nor­mal­iza­tion con­di­tion:

$${\textstyle\frac{1}{2}} \epsilon_0 \int_{\rm all} \left( ... ...ight\vert^2 \right){ \rm d}^3{\skew0\vec r} = \hbar\omega %$$ (A.158)

Con­sider how this works out for the ex­am­ple eigen­func­tion of def­i­nite lin­ear mo­men­tum men­tioned above. That eigen­func­tion can­not be nor­mal­ized in in­fi­nite space since it does not go to zero at large dis­tances. To nor­mal­ize it, you have to as­sume that the elec­tro­mag­netic field is con­fined to a big pe­ri­odic box of vol­ume ${\cal V}$. In that case the nor­mal­ized eigen­func­tion and un­ob­serv­able fields be­come:

$$\skew3\vec A_\gamma^{\rm n}= \frac{\varepsilon_k}{{\rm i}kc... ...arepsilon_k = \sqrt{\frac{\hbar\omega}{\epsilon_0{\cal V}}} %$$ (A.159)

An­other in­ter­est­ing ex­am­ple is given in {A.21.6}. It is a pho­ton state with def­i­nite an­gu­lar mo­men­tum $\hbar$ in the di­rec­tion of mo­tion. Such a pho­ton state is called right-cir­cu­larly po­lar­ized. In this ex­am­ple the lin­ear mo­men­tum is taken to be in the $z$-​di­rec­tion, rather than the $y$-​di­rec­tion. The nor­mal­ized wave func­tion and un­ob­serv­able fields are:

$$\skew3\vec A_\gamma^{\rm n}= \frac{\varepsilon_k}{{\rm i}kc... ...arepsilon_k = \sqrt{\frac{\hbar\omega}{\epsilon_0{\cal V}}} %$$ (A.160)

It will be in­ter­est­ing to see what the ob­serv­able fields for this pho­ton state look like.

A.23.3 The elec­tro­mag­netic op­er­a­tors

The pre­vi­ous sub­sec­tion has iden­ti­fied the form of the wave func­tion of a pho­ton in an en­ergy eigen­state. The next step is to iden­tify the Hamil­ton­ian op­er­a­tors of the ob­serv­able elec­tric and mag­netic fields.

But first there is a prob­lem. If you have ex­actly one pho­ton, the wave func­tions as dis­cussed in the pre­vi­ous sub­sec­tion would do just fine. If you had ex­actly two pho­tons, you could read­ily write a wave func­tion for them too. But a state with an ex­act num­ber $i$ of pho­tons is an en­ergy eigen­state. It has en­ergy $i\hbar\omega$, tak­ing the zero of en­ergy as the state of no pho­tons. En­ergy eigen­states are sta­tion­ary, chap­ter 7.1.4. They never change. All the in­ter­est­ing me­chan­ics in na­ture is due to un­cer­tainty in en­ergy. As far as pho­tons are con­cerned, that re­quires un­cer­tainty in the num­ber of pho­tons. And there is no way to write a wave func­tion for an un­cer­tain num­ber of par­ti­cles in clas­si­cal quan­tum me­chan­ics. The math­e­mat­i­cal ma­chin­ery is sim­ply not up to it.

The math­e­mat­ics of quan­tum field the­ory is needed, as dis­cussed in ad­den­dum {A.15}. The key con­cepts will be briefly sum­ma­rized here. The math­e­mat­ics starts with Fock space kets. Con­sider a sin­gle en­ergy eigen­func­tion for pho­tons, like one of the ex­am­ples given in the pre­vi­ous sub­sec­tion. The Fock space ket

$${\left\vert i\right\rangle}$$

in­di­cates the wave func­tion if there are ex­actly $i$ pho­tons in the con­sid­ered en­ergy eigen­func­tion. The num­ber $i$ is called the oc­cu­pa­tion num­ber of the state. (If more than one pho­ton state is of in­ter­est, an oc­cu­pa­tion num­ber is added to the ket for each state. How­ever, the dis­cus­sion here will stay re­stricted to a sin­gle state.)

The Fock space ket for­mal­ism al­lows wave func­tions to be writ­ten for any num­ber of par­ti­cles in the state. And by tak­ing lin­ear com­bi­na­tions of kets with dif­fer­ent oc­cu­pa­tion num­bers, un­cer­tainty in the num­ber of pho­tons can be de­scribed. So un­cer­tainty in en­ergy can be de­scribed.

Kets are taken to be or­tho­nor­mal. The in­ner prod­uct ${\left\langle i_1\right.\hspace{-\nulldelimiterspace}}{\left\vert i_2\right\rangle}$ of two kets with dif­fer­ent oc­cu­pa­tion num­bers $i_1$ and $i_2$ is zero. The in­ner prod­uct of a ket with it­self is taken to be one. That is ex­actly the same as for en­ergy eigen­func­tions in clas­si­cal quan­tum me­chan­ics,

Next, it turns out that op­er­a­tors that act on pho­ton wave func­tions are in­trin­si­cally linked to op­er­a­tors that an­ni­hi­late and cre­ate pho­tons. Math­e­mat­i­cally, at least. These op­er­a­tors are de­fined by the re­la­tions

$$\widehat a{\left\vert i\right\rangle} = \sqrt{i} {\left\ver... ...t i{-}1\right\rangle} = \sqrt{i} {\left\vert i\right\rangle} %$$ (A.161)

for any num­ber of pho­tons $i$. In words, the an­ni­hi­la­tion op­er­a­tor $\widehat a$ takes a state of $i$ pho­tons and turns it into a state with one less pho­ton. The cre­ation op­er­a­tor $\widehat a^\dagger$ puts the pho­ton back in. The scalar fac­tors $\sqrt{i}$ are a mat­ter of con­ve­nience. If you did not put them in here, you would have to do it else­where.

At first it may seem just weird that there are phys­i­cal op­er­a­tors like that. But a bit more thought may make it more plau­si­ble. First of all, na­ture pretty much forces the Fock space kets on us. Clas­si­cal quan­tum me­chan­ics would like to num­ber par­ti­cles such as pho­tons just like clas­si­cal physics likes to do: pho­ton 1, pho­ton 2, ... But na­ture makes a farce out of that with the sym­metriza­tion re­quire­ment. It al­lows ab­solutely no dif­fer­ence in the way one pho­ton oc­cu­pies a state com­pared to an­other one. In­deed, na­ture goes to such a length of pre­vent­ing us to, God for­bid, make a dis­tinc­tion be­tween one pho­ton and an­other that she puts every sin­gle pho­ton in the uni­verse partly in every sin­gle mi­cro­scopic pho­ton state on earth. Now Fock space kets are the only way to ex­press how many pho­tons are in a given state with­out say­ing which pho­tons. And if the sym­bols of na­ture are then ap­par­ently Fock space kets, the op­er­a­tors of na­ture are pretty un­avoid­ably an­ni­hi­la­tion and cre­ation op­er­a­tors. There is not much else you can do with Fock space kets than change the num­ber of par­ti­cles.

The an­ni­hi­la­tion and cre­ation op­er­a­tors are not Her­mit­ian. They can­not be taken un­changed to the other side of an in­ner prod­uct of kets. How­ever, they are Her­mit­ian con­ju­gates: they change into each other when taken to the other side of an in­ner prod­uct:

$$\Big\langle {\left\vert i_2\right\rangle} \Big\vert\widehat... ...}\right\vert} \widehat a^\dagger {\left\vert i_2\right\rangle}$$

To see this, note that the in­ner prod­ucts are only nonzero if $i_2$ $\vphantom0\raisebox{1.5pt}{$=$}$ $i_1-1$ be­cause of the or­thog­o­nal­ity of kets with dif­fer­ent num­bers of pho­tons. And if $i_2$ $\vphantom0\raisebox{1.5pt}{$=$}$ $i_1-1$, then (A.161) shows that all four in­ner prod­ucts above equal $\sqrt{i_1}$.

That is im­por­tant be­cause it shows that Her­mit­ian op­er­a­tors can be formed from com­bi­na­tions of the two op­er­a­tors. For ex­am­ple, $\widehat a+\widehat a^\dagger$ is a Her­mit­ian op­er­a­tor. Each of the two op­er­a­tors changes into the other when taken to the other side of an in­ner prod­uct. So the sum stays un­changed. More gen­er­ally, if $c$ is any real or com­plex num­ber, $\widehat a{c}+\widehat a^\dagger {c}^*$ is Her­mit­ian.

And that then is the ba­sic recipe for find­ing the op­er­a­tors of the ob­serv­able elec­tric and mag­netic fields. Take $\widehat a$ times the un­ob­serv­able field of the nor­mal­ized pho­ton state, (A.157) with (A.158) and (A.155). Add the Her­mit­ian con­ju­gate of that. And put in the usual 1$\raisebox{.5pt}{$/$}$​$\sqrt{2}$ fac­tor of quan­tum me­chan­ics for av­er­ag­ing states. In to­tal

$$\fbox{$\displaystyle \skew6\widehat{\skew3\vec{\cal E}}= \... ...hat a^\dagger \skew2\vec{\cal B}_\gamma^{\rm{n}*}\right) $} %$$ (A.162)

You might won­der why there are two terms in the op­er­a­tors, one with a com­plex con­ju­gate wave func­tion. Math­e­mat­i­cally that is def­i­nitely needed to get Her­mit­ian op­er­a­tors. That in turn is needed to get real ob­served fields. But what does it mean phys­i­cally? One way of think­ing about it is that the ob­served field is real be­cause it does not just in­volve an in­ter­ac­tion with an $e^{{\rm i}({\vec k}\cdot{\skew0\vec r}-{\omega}t)}$ pho­ton, but also with an $e^{-{\rm i}({\vec k}\cdot{\skew0\vec r}-{\omega}t)}$ an­tipho­ton.

Of course, just be­cause the above op­er­a­tors are Her­mit­ian does not prove that they are the right ones for the ob­serv­able elec­tric and mag­netic fields. Un­for­tu­nately, there is no straight­for­ward way to de­duce quan­tum me­chan­ics op­er­a­tors from mere knowl­edge of the clas­si­cal ap­prox­i­ma­tion. Vice-versa is not a prob­lem: given the op­er­a­tors, it is fairly straight­for­ward to de­duce the cor­re­spond­ing clas­si­cal equa­tions for a macro­scopic sys­tem. It is much like at the start of this book, where it was pos­tu­lated that the mo­men­tum of a par­ti­cle cor­re­sponds to the op­er­a­tor $\hbar\partial$$\raisebox{.5pt}{$/$}$​${\rm i}\partial{x}$. That was a leap of faith. How­ever, it was even­tu­ally seen that it did pro­duce the cor­rect clas­si­cal mo­men­tum for macro­scopic sys­tems, chap­ter 7.2.1 and 7.10, as well as cor­rect quan­tum re­sults like the en­ergy lev­els of the hy­dro­gen atom, chap­ter 4.3. A sim­i­lar leap of faith will be needed to quan­tize the elec­tro­mag­netic field.

A.23.4 Prop­er­ties of the ob­serv­able elec­tro­mag­netic field

The pre­vi­ous sub­sec­tion pos­tu­lated the op­er­a­tors (A.162) for the ob­serv­able elec­tric and mag­netic fields. This sub­sec­tion will ex­am­ine the con­se­quences of these op­er­a­tors, in or­der to gain con­fi­dence in them. And to learn some­thing about the ef­fects of quan­ti­za­tion of the elec­tro­mag­netic field.

Con­sider first a sim­ple wave func­tion where there are ex­actly $i$ pho­tons in the con­sid­ered pho­ton state. In terms of Fock space kets, the wave func­tion is then:

$$\Psi = c_i e^{-{\rm i}i\omega t} {\left\vert i\right\rangle}$$

where $c_i$ is a con­stant with mag­ni­tude 1. This fol­lows the Schrö­din­ger rule that the time de­pen­dence in a wave func­tion of def­i­nite en­ergy $E$ is given by $e^{-{{\rm i}}Et/\hbar}$, with in this case $E$ $\vphantom0\raisebox{1.5pt}{$=$}$ $i\hbar\omega$.

The ex­pec­ta­tion value of the elec­tric field at a given po­si­tion and time is then by de­f­i­n­i­tion

$$\langle \skew3\vec{\cal E}\rangle = \Big\langle\Psi\Big\ve... ...\right) c_i e^{-{\rm i}i\omega t} {\left\vert i\right\rangle}$$

That is zero be­cause $\widehat a$ and $\widehat a^\dagger$ turn the right hand ket into ${\left\vert i{-}1\right\rangle}$ re­spec­tively ${\left\vert i{+}1\right\rangle}$. These are or­thog­o­nal to the left hand ${\left\langle i\hspace{0.3pt}\right\vert}$. The same way, the ex­pec­ta­tion mag­netic field will be zero too.

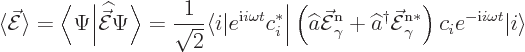
Oops.

Zero elec­tric and mag­netic fields were not ex­actly ex­pected if there is a nonzero num­ber of pho­tons present.

No panic please. This is an en­ergy eigen­state. Of­ten these do not re­sem­ble clas­si­cal physics at all. Think of a hy­dro­gen atom in its ground state. The ex­pec­ta­tion value of the lin­ear mo­men­tum of the elec­tron is zero in that state. That is just like the elec­tric and mag­netic fields are zero here. But the ex­pec­ta­tion value of the square mo­men­tum of the hy­dro­gen elec­tron is not zero. In fact, that gives the nonzero ex­pec­ta­tion value of the ki­netic en­ergy of the elec­tron, 13.6 eV. So maybe the square fields need to be ex­am­ined here.

Come to think of it, the first thing to check should ob­vi­ously have been the en­ergy. It bet­ter be $i\hbar\omega$ for $i$ pho­tons. Fol­low­ing the New­ton­ian anal­ogy for the clas­si­cal en­ergy in­te­gral (A.152), the Hamil­ton­ian should be

$$H = {\textstyle\frac{1}{2}} \epsilon_0 \int_{\rm all} \left... ...\widehat{\skew2\vec{\cal B}}^2\right){ \rm d}^3{\skew0\vec r}$$

This can be greatly sim­pli­fied by plug­ging in the given ex­pres­sions for the op­er­a­tors and iden­ti­fy­ing the in­te­grals, {D.40}:

$$\fbox{$\displaystyle H = {\textstyle\frac{1}{2}}\hbar\omeg... ...hat a^\dagger \widehat a+ \widehat a\widehat a^\dagger ) $} %$$ (A.163)

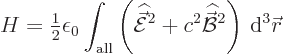
Now ap­ply this Hamil­ton­ian on a state with $i$ pho­tons. First, us­ing the de­f­i­n­i­tions (A.161) of the an­ni­hi­la­tion and cre­ation op­er­a­tors

$$\widehat a^\dagger \widehat a{\left\vert i\right\rangle} = ... ...t\vert i{+}1\right\rangle}) = (i+1){\left\vert i\right\rangle}$$

This shows that the op­er­a­tors $\widehat a$ and $\widehat a^\dagger$ do not com­mute; their or­der makes a dif­fer­ence. In par­tic­u­lar, ac­cord­ing to the above their com­mu­ta­tor equals

$$[\widehat a,\widehat a^\dagger ]\equiv \widehat a\widehat a^\dagger - \widehat a^\dagger \widehat a= 1 %$$ (A.164)

Any­way, us­ing the above re­la­tions the ex­pres­sion for the Hamil­ton­ian ap­plied on a Fock space ket be­comes

$$H {\left\vert i\right\rangle} = \hbar\omega(i+{\textstyle\frac{1}{2}}) {\left\vert i\right\rangle}$$

The fac­tor in front of the fi­nal ket is the en­ergy eigen­value. It is more or less like ex­pected, which was $i\hbar\omega$ for $i$ pho­tons. But there is an­other one-half pho­ton worth of en­ergy.

That, how­ever, may be cor­rect. It closely re­sem­bles what hap­pened for the har­monic os­cil­la­tor, chap­ter 4.1. Ap­par­ently the en­ergy in the elec­tro­mag­netic field is never zero, just like a har­monic os­cil­la­tor is never at rest. The en­ergy in­creases by $\hbar\omega$ for each ad­di­tional pho­ton as it should.

Ac­tu­ally, the half pho­ton vac­uum en­ergy is some­what of a prob­lem. If you start sum­ming these half pho­tons over all in­fi­nitely many fre­quen­cies, you end up, of course, with in­fin­ity. Now the ground state en­ergy does not af­fect the dy­nam­ics. But if you do mea­sure­ments of the elec­tric or mag­netic fields in vac­uum, you will get nonzero val­ues. So ap­par­ently there is real en­ergy there. Pre­sum­ably that should af­fect grav­ity. Maybe the ef­fect would not be in­fi­nite, if you cut off the sum at fre­quen­cies at which quan­tum me­chan­ics might fail, but it should cer­tainly be ex­tremely dra­matic. So why is it not ob­served? The an­swer is un­known. See chap­ter 8.7 for one sug­ges­tion.

The vac­uum en­ergy also has con­se­quences if you place two con­duct­ing plates ex­tremely closely to­gether. The con­duct­ing plates re­strict the vac­uum field be­tween the plates. (Or at least the rel­a­tively low en­ergy part of it. Be­yond say the X-ray range pho­tons will not no­tice the plates.) Be­cause of the re­stric­tion of the plates, you would ex­pect the vac­uum en­ergy to be less than ex­pected. Be­cause of en­ergy con­ser­va­tion, that must mean that there is an at­trac­tive force be­tween the plates. That is the so-called “Casimir force.” This weird force has ac­tu­ally been mea­sured ex­per­i­men­tally. Once again it is seen that the half pho­ton of vac­uum en­ergy in each state is not just a math­e­mat­i­cal ar­ti­fact.

Be­cause of the in­fi­nite en­ergy, some au­thors de­scribe the vac­uum as a “seething caul­dron” of elec­tro­mag­netic waves. These au­thors may not be aware that the vac­uum state, be­ing a ground state, is sta­tion­ary. Or they may not have ac­cess to a dic­tio­nary of the Eng­lish lan­guage.

The next test of the field op­er­a­tors is to re­con­sider the ex­pec­ta­tion elec­tric field when there is un­cer­tainty in en­ergy. Also re­mem­ber to add an­other half pho­ton of en­ergy now. Then the gen­eral wave func­tion takes the form:

$$\Psi = \sum_i c_i e^{-{\rm i}(i+\frac12)\omega t} {\left\vert i\right\rangle}$$

The ex­pec­ta­tion value of the elec­tric field fol­lows as

$$\langle \skew3\vec{\cal E}\rangle = \sum_i \sum_j \frac{1}{... ..._j e^{-{\rm i}(j+\frac12)\omega t} {\left\vert j\right\rangle}$$

Us­ing the de­f­i­n­i­tions of the an­ni­hi­la­tion and cre­ation op­er­a­tors and the or­tho­nor­mal­ity of the kets, this can be worked out fur­ther to

$$\langle \skew3\vec{\cal E}\rangle = Ce^{-{\rm i}\omega t}\... ...d C \equiv \frac{1}{\sqrt{2}} \sum_i c_{i-1}^* c_i \sqrt{i} %$$ (A.165)

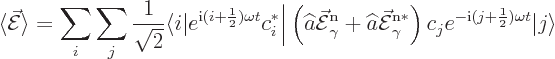
Well, the field is no longer zero. Note that the first term in the elec­tric field is more or less what you would ex­pect from the un­ob­serv­able field of a sin­gle pho­ton. But the ob­serv­able field adds the com­plex con­ju­gate. That makes the ob­serv­able field real.

The prop­er­ties of the ob­serv­able fields can now be de­ter­mined. For ex­am­ple, con­sider the pho­ton wave func­tion (A.159) given ear­lier. This wave func­tion had its lin­ear mo­men­tum in the $y$-​di­rec­tion. It was “lin­early po­lar­ized” in the $z$-​di­rec­tion. Ac­cord­ing to the above ex­pres­sion, the ob­serv­able elec­tric field is:

$$\langle \skew3\vec{\cal E}\rangle = {\hat k}\varepsilon_k ... ...^{{\rm i}(ky-\omega t)} + C^* e^{-{\rm i}(ky-\omega t)}\right)$$

The first term is roughly what you would want to write down for the un­ob­serv­able elec­tric field of a sin­gle pho­ton. The sec­ond term, how­ever, is the com­plex con­ju­gate of that. It makes the ob­serv­able field real. Writ­ing $C$ in the form $\vert C\vert e^{{\rm i}\alpha}$ and us­ing the Euler for­mula 2.5 to clean up gives:

$$\langle \skew3\vec{\cal E}\rangle = {\hat k}2 \varepsilon_k \vert C\vert \cos(ky-\omega t + \alpha)$$

That is a real elec­tro­mag­netic wave. It is still po­lar­ized in the $z$-​di­rec­tion, and it trav­els in the $y$-​di­rec­tion.

The cor­re­spond­ing mag­netic field goes ex­actly the same way. The only dif­fer­ence in (A.159) is that ${\hat k}$ gets re­placed by ${\hat\imath}$. There­fore

$$\langle c \skew2\vec{\cal B}\rangle = {\hat\imath}2 \varepsilon_k \vert C\vert \cos(ky-\omega t + \alpha)$$

Note that like for the pho­ton wave func­tion, the ob­serv­able fields are nor­mal to the di­rec­tion of wave prop­a­ga­tion, and to each other.

As an­other ex­am­ple, con­sider the “cir­cu­larly po­lar­ized” pho­ton wave func­tion (A.160). This wave func­tion had its lin­ear mo­men­tum in the $z$-​di­rec­tion, and it had def­i­nite an­gu­lar mo­men­tum $\hbar$ around the $z$-​axis. Here the ob­serv­able fields are found to be

$$\begin{eqnarray*} & \langle \skew3\vec{\cal E}\rangle = \sqrt{2} \varepsilon_k ... ...z-\omega t +\alpha)+{\hat\jmath}\cos(kz-\omega t +\alpha)\right] \end{eqnarray*}$$

Like for lin­early po­lar­ized light, the elec­tric and mag­netic fields are nor­mal to the di­rec­tion of wave prop­a­ga­tion and to each other. But here the elec­tric and mag­netic field vec­tors ro­tate around in a cir­cle when seen at a fixed po­si­tion $z$. Seen at a fixed time, the end points of the elec­tric vec­tors that start from the $z$-​axis form a he­lix. And so do the mag­netic ones.

The fi­nal ques­tion is un­der what con­di­tions you would get a clas­si­cal elec­tro­mag­netic field with rel­a­tively lit­tle quan­tum un­cer­tainty. To an­swer that, first note that the square quan­tum un­cer­tainty is given by

$$\sigma_\skew3\vec{\cal E}^2 = \langle\skew3\vec{\cal E}^2\rangle - \langle\skew3\vec{\cal E}\rangle^2$$

(This is the square of chap­ter 4.4.3 (4.44) mul­ti­plied out and iden­ti­fied.)

To eval­u­ate this un­cer­tainty re­quires the ex­pec­ta­tion value of the square elec­tric field. That can be found much like the ex­pec­ta­tion value (A.165) of the elec­tric field it­self. The an­swer is

$$\langle \skew3\vec{\cal E}^2 \rangle = 2 D_0 \vert\skew3\v... ...* e^{2{\rm i}\omega t}(\skew3\vec{\cal E}_\gamma^{\rm {n}*})^2$$

where

$$D_0 \equiv \frac{1}{2} \sum_i \vert c_i\vert^2 (i+{\textsty... ...equiv \frac{1}{2} \sum_i c_{i-1}^* c_{i+1} \sqrt{i} \sqrt{i+1}$$

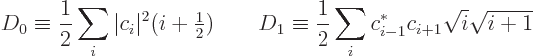
Note that when this is sub­sti­tuted into the in­te­gral (A.152) for the en­ergy, the $D_0$ term gives half the ex­pec­ta­tion value of the en­ergy. In par­tic­u­lar, the co­ef­fi­cient $D_0$ it­self is half the ex­pec­ta­tion value of the $i+\frac12$ num­ber of pho­tons of en­ergy. The other half comes from the cor­re­spond­ing term in the mag­netic field. The $D_1$ terms above in­te­grate away against the cor­re­spond­ing terms in the mag­netic field, {D.40}.

To de­ter­mine the un­cer­tainty in the elec­tric field, it is con­ve­nient to write the ex­pec­ta­tion square elec­tric field above in real form. To do so, the co­ef­fi­cient $D_1$ is writ­ten in the form $\vert D_1\vert e^{2{\rm i}\beta}$. Also, the square un­ob­serv­able elec­tric field $(\skew3\vec{\cal E}_\gamma^{\rm {n}})^2$ is writ­ten in the form $\vert\skew3\vec{\cal E}_\gamma^{\rm {n}}\vert^2e^{2{\rm i}\gamma}$. Here $\gamma$ will nor­mally de­pend on po­si­tion; for ex­am­ple $\gamma$ $\vphantom0\raisebox{1.5pt}{$=$}$ $ky$ for the given ex­am­ple of lin­early po­lar­ized light.

Then the ex­pec­ta­tion square elec­tric field be­comes, us­ing the Euler for­mula (2.5) and some trig,

$$\langle \skew3\vec{\cal E}^2 \rangle = 2 (D_0-\vert D_1\ve... ...cal E}_\gamma^{\rm {n}}\vert^2 \cos^2(\gamma-\omega t + \beta)$$

with $D_0$ and $D_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\vert D_1\vert e^{2{\rm i}\beta}$ as given above. Sim­i­larly the square of the ex­pec­ta­tion elec­tric field, as given ear­lier in (A.165), can be writ­ten as

$$\langle \skew3\vec{\cal E}\rangle^2 = 4 \vert C\vert^2 \ve... ...m i}\alpha} = \frac{1}{\sqrt{2}} \sum_i c_{i-1}^* c_i \sqrt{i}$$

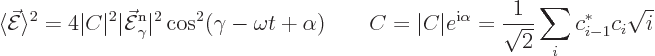
For a field with­out quan­tum un­cer­tainty, $\langle\skew3\vec{\cal E}^2\rangle$ and $\langle\skew3\vec{\cal E}\rangle^2$ as given above must be equal. Note that first of all this re­quires that $\vert D_1\vert$ $\vphantom0\raisebox{1.5pt}{$=$}$ $D_0$, be­cause oth­er­wise $\langle\skew3\vec{\cal E}^2\rangle$ does not be­come zero pe­ri­od­i­cally like $\langle\skew3\vec{\cal E}\rangle^2$ does. Also $\beta$ will have to be $\alpha$, up to a whole mul­ti­ple of $\pi$, oth­er­wise the ze­ros are not at the same times. Fi­nally, $\vert C\vert$ will have to be equal to $D_0$ too, or the am­pli­tudes will not be the same.

How­ever, re­gard­less of un­cer­tainty, the co­ef­fi­cients must al­ways sat­isfy

$$\vert D_1\vert \mathrel{\raisebox{-.7pt}{$\leqslant$}}D_0 \... ...pt}{$\leqslant$}}{\textstyle\frac{1}{2}} (D_0+\vert D_1\vert)$$

The first in­equal­ity ap­plies be­cause oth­er­wise $\langle\skew3\vec{\cal E}^2\rangle$ would be­come neg­a­tive when­ever the co­sine is zero. The sec­ond ap­plies be­cause $\langle\skew3\vec{\cal E}\rangle^2$ can­not be larger than $\langle\skew3\vec{\cal E}^2\rangle$; the square un­cer­tainty can­not be neg­a­tive. For quan­tum cer­tainty then, the above re­la­tions must be­come equal­i­ties. How­ever, a care­ful analy­sis shows that they can­not be­come equal­i­ties, {D.40}.

So there is al­ways some quan­tum un­cer­tainty left. Max­i­mum un­cer­tainty oc­curs when the num­ber of pho­tons has a def­i­nite value. Then $D_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ $C$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0.

If there is al­ways at least some un­cer­tainty, the real ques­tion is un­der what con­di­tions it is rel­a­tively small. Analy­sis shows that the un­cer­tainty in the fields is small un­der the fol­low­ing con­di­tions, {D.40}:

• The ex­pec­ta­tion value of the num­ber of pho­tons $\left\langle{i}\right\rangle$ is large enough.
• Non­neg­li­gi­ble co­ef­fi­cients $c_i$ are lim­ited to a rel­a­tively small range around $i$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\left\langle{i}\right\rangle$. How­ever, that range must still con­tain a rel­a­tively large num­ber of co­ef­fi­cients.
• The co­ef­fi­cients for suc­ces­sive val­ues of $i$ are dif­fer­ent by a fac­tor that is ap­prox­i­mately equal to $e^{{\rm i}\alpha}$.

In that case clas­si­cal elec­tric and mag­netic field re­sult with lit­tle quan­tum un­cer­tainty. Note that the above con­di­tions ap­ply for pho­tons re­stricted to a sin­gle quan­tum state. In a real elec­tro­mag­netic field, many quan­tum states would be oc­cu­pied and things would be much messier still.

It may also be noted that the above con­di­tions bear a strik­ing re­sem­blance to the con­di­tions that pro­duce a par­ti­cle with a fairly co­her­ent po­si­tion and mo­men­tum in clas­si­cal quan­tum me­chan­ics, chap­ter 7.10.