| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.24 Quantum spontaneous emission
Chapter 7.8 explained the general interaction between
atoms and electromagnetic fields. However, spontaneous emission of
radiation was found using a dirty trick due to Einstein. He peeked at
the solution for blackbody radiation. This addendum will give a
proper quantum description. Warning: while this addendum tries to be
reasonably self-contained, to really appreciate the details you may
have to read some other addenda too.
The problem with the descriptions of emission and absorption of
radiation in chapter 7.7 and 7.8 is that they
assume that the electromagnetic field is given. The electromagnetic
field is not given; it changes by one photon. That is rather
important for spontaneous emission, where it changes from no photons
to one photon. To account for that correctly requires that the
electromagnetic field is properly quantized. That is done in this
note.
To keep it simple, it will be assumed that the atom is a hydrogen one.
Then there is just one electron to worry about. (The general analysis
can be found in {A.25}). The hydrogen atom is
initially in some high energy state 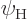 . Then it
emits a photon and transitions to a lower energy state
. Then it
emits a photon and transitions to a lower energy state
 . The emitted photon comes out in a state with
energy
. The emitted photon comes out in a state with
energy
Recall that the photon energy is given in terms of its frequency
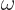 by the Planck-Einstein relation. This photon energy is
approximately the difference between the atomic energies. It does not
have to be exact; there can be some energy slop, chapter
7.6.1.
by the Planck-Einstein relation. This photon energy is
approximately the difference between the atomic energies. It does not
have to be exact; there can be some energy slop, chapter
7.6.1.
Only a single photon energy state needs to be considered at a time.
At the end of the story, the results can be summed over all possible
photon states. To allow for stimulated emission, it will be assumed
that initially there may already be  preexisting photons present.
For spontaneous emission,
preexisting photons present.
For spontaneous emission, 
 0. The initial system state will be
indicated as:
0. The initial system state will be
indicated as:
Here the so-called Fock space ket 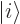 is simply a concise way of
indicating that there are
is simply a concise way of
indicating that there are  photons in the considered photon quantum
state.
photons in the considered photon quantum
state.
In the final state the atom has decayed to a lower energy state
 . In doing so it has released 1 more photon into
the considered photon state. So the final wave function is
. In doing so it has released 1 more photon into
the considered photon state. So the final wave function is
The key to the emission process is now the set of Hamiltonian
coefficients, chapter 7.6,
Here 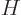 is the Hamiltonian. All that really needs to be done in this
note is to identify these coefficients, and in particular the
so-called matrix element
is the Hamiltonian. All that really needs to be done in this
note is to identify these coefficients, and in particular the
so-called matrix element 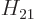 . With the matrix element
known, Fermi’s golden rule can be used to find the precise
transition rate, chapter 7.6.1.
. With the matrix element
known, Fermi’s golden rule can be used to find the precise
transition rate, chapter 7.6.1.
To identify the Hamiltonian coefficients, first the Hamiltonian must
be identified. Recall that the Hamiltonian is the operator of the
total energy of the system. It will take the form
The first term in the right hand side is the inherent energy of the
hydrogen atom. This Hamiltonian was written down way back in chapter
4.3. However, its precise form is of no interest here. The
second term in the right hand side is the energy in the
electromagnetic field. Electromagnetic fields too have inherent
energy, about 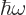 per photon in fact. The third term is the
energy of the interaction between the atomic electron and the
electromagnetic field.
per photon in fact. The third term is the
energy of the interaction between the atomic electron and the
electromagnetic field.
Unlike the first term in the Hamiltonian, the other two are inherently
relativistic: the number of photons is hardly a conserved quantity.
Photons are readily created or absorbed by a charged particle, like
the electron here. And it turns out that Hamiltonians for photons are
intrinsically linked to operators that annihilate and create photons.
Mathematically, at least. These operators are defined by the
relations
 |
(A.166) |
for any number of photons  . In words, the annihilation
operator
. In words, the annihilation
operator 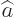 takes a state of
takes a state of  photons and turns it into a state
with one less photon. The creation operator
photons and turns it into a state
with one less photon. The creation operator  puts the photon
back in. The scalar factors
puts the photon
back in. The scalar factors 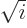 are a matter of convenience.
If you did not put them in here, you would have to do it elsewhere.
are a matter of convenience.
If you did not put them in here, you would have to do it elsewhere.
The Hamiltonian that describes the inherent energy in the electromagnetic
field turns out to be, {A.23},
As a sanity check, this Hamiltonian can be applied on a state of  photons. Using the definitions of the annihilation and creation
operators given above,
photons. Using the definitions of the annihilation and creation
operators given above,
The factor in front of the final ket is the energy eigenvalue. So
the energy in the field increases by one unit 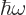 for each
photon added, exactly as it should. The additional half photon is the
ground state energy of the electromagnetic field. Even in its ground
state, the electromagnetic field has some energy left. That is much
like a one-dimensional harmonic oscillator still has
for each
photon added, exactly as it should. The additional half photon is the
ground state energy of the electromagnetic field. Even in its ground
state, the electromagnetic field has some energy left. That is much
like a one-dimensional harmonic oscillator still has
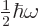 of energy left in its ground state, chapter
4.1.
of energy left in its ground state, chapter
4.1.
Finally the energy of the interaction between the electron and
electromagnetic field is needed. This third part of the total
Hamiltonian is the messiest. To keep it as simple as possible, it
will assumed that the transition is of the normal electric dipole
type. In such transitions the electron interacts only with the
electric part of the electromagnetic field. In addition, just like in
the analysis of chapter 7.7.1 using a classical
electromagnetic field, it will be assumed that the electric field is
in the  -direction and propagates in the
-direction and propagates in the  -direction. (The
general multipole analysis can be found in {A.25}).
-direction. (The
general multipole analysis can be found in {A.25}).
Now recall that in quantum mechanics, observable properties of
particles are the eigenvalues of Hermitian operators, chapter
3.3. For example, the observable values of linear momentum
of an electron in the  -direction are the eigenvalues of the linear
momentum operator
-direction are the eigenvalues of the linear
momentum operator 

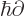

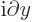 .
This operator acts on the electron wave function.
.
This operator acts on the electron wave function.
Similarly, the electric field 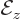 that the electron interacts with
is an observable property of the corresponding photons. So the
observable values of the electric field must be the eigenvalues of a
Hermitian electric field operator
that the electron interacts with
is an observable property of the corresponding photons. So the
observable values of the electric field must be the eigenvalues of a
Hermitian electric field operator 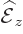 . And this operator acts on
photon wave functions.
. And this operator acts on
photon wave functions.
In the analysis using a classical electromagnetic field, the energy of
interaction between the electron and the electromagnetic field was
taken to be approximately 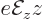 . That is similar to the
. That is similar to the 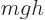 potential of a particle due to gravity. The electron electric charge
potential of a particle due to gravity. The electron electric charge

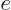 takes the place of the mass
takes the place of the mass  , the electric field
, the electric field 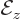 that of the acceleration of gravity
that of the acceleration of gravity 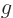 , and
, and  that of the height
that of the height
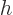 . Using the quantized electric field, there is no given classical
field
. Using the quantized electric field, there is no given classical
field 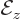 , and instead the operator
, and instead the operator 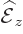 must be used:
must be used:
The operator 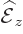 acts on the ket part of the combined atom-photon
wave function. (And, although you may not think of it that way, the
factor
acts on the ket part of the combined atom-photon
wave function. (And, although you may not think of it that way, the
factor  is really an operator that acts on the electron wave
function part. That is true even in the analysis using the classical
field.)
is really an operator that acts on the electron wave
function part. That is true even in the analysis using the classical
field.)
The electric field operator 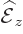 can be identified from the
appropriate photon wave function. The photon wave function here is
assumed to have its linear momentum in the
can be identified from the
appropriate photon wave function. The photon wave function here is
assumed to have its linear momentum in the  -direction and its
unobservable electric field in the
-direction and its
unobservable electric field in the  -direction. The
corresponding normalized wave function and unobservable electric field
were given in {A.21.6} (A.95):
-direction. The
corresponding normalized wave function and unobservable electric field
were given in {A.21.6} (A.95):
Here 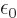 is the permittivity of space. Also
is the permittivity of space. Also 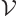 is the
volume of the large periodic box in which the entire system will be
assumed to be located. In truly infinite space the analysis would be
extremely messy, littered with ugly delta functions.
is the
volume of the large periodic box in which the entire system will be
assumed to be located. In truly infinite space the analysis would be
extremely messy, littered with ugly delta functions.
The rules to get the operator of the observable electric field were
discussed in addendum {A.23}. First the unobservable
electric field above is multiplied by the annihilation operator, then
the Hermitian conjugate of that product is added, and the sum is
divided by 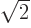 :
:
(Note that for the usual Schrödinger approach followed here, time
dependence is described by the wave function. Most sources switch
here to a Heisenberg approach where the time-dependence is pushed into
the operators. There is however no particular need to do so.)
In the electric dipole approximation, it is assumed that the atom is
so small compared to the wave length of the photon that 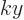 can be
assumed to be zero. Therefore
can be
assumed to be zero. Therefore
The combined Hamiltonian is then
with the first two terms as described earlier.
Next the Hamiltonian matrix coefficients are needed. The first one is
Now the atomic part of the Hamiltonian produces a mere factor
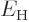 when it acts on the atomic part of the right hand wave
function. Further, as discussed above, the electromagnetic
Hamiltonian produces a factor
when it acts on the atomic part of the right hand wave
function. Further, as discussed above, the electromagnetic
Hamiltonian produces a factor 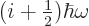 when it acts on
the right hand ket. Finally the interaction part of the Hamiltonian
does not produce a contribution. One way to see that is from the
atomic inner product. The atomic inner product is zero because
negative values of
when it acts on
the right hand ket. Finally the interaction part of the Hamiltonian
does not produce a contribution. One way to see that is from the
atomic inner product. The atomic inner product is zero because
negative values of  integrate away against positive ones. Another
way to see it is from the electromagnetic inner product. The
operators
integrate away against positive ones. Another
way to see it is from the electromagnetic inner product. The
operators 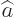 and
and  produce states
produce states 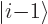 respectively
respectively
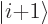 when they act on the right hand ket. And those are
orthogonal to the left hand ket; inner products between kets with
different numbers of photons are zero. Kets are by definition
orthonormal.
when they act on the right hand ket. And those are
orthogonal to the left hand ket; inner products between kets with
different numbers of photons are zero. Kets are by definition
orthonormal.
All together then
The same way
Finally the matrix element:
In this case the atomic part of the Hamiltonian produces zero. The
reason is that this Hamiltonian produces a simple scalar factor
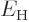 when it acts on the right hand state. It leaves the
state
when it acts on the right hand state. It leaves the
state 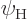 itself unchanged. And this state produces zero
in an inner product with the atomic state
itself unchanged. And this state produces zero
in an inner product with the atomic state  ;
energy eigenstates are orthonormal. Similarly, the electromagnetic
Hamiltonian produces zero. It leaves the ket
;
energy eigenstates are orthonormal. Similarly, the electromagnetic
Hamiltonian produces zero. It leaves the ket 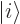 in the right
hand wave wave function unchanged, and that is orthogonal to the left
hand
in the right
hand wave wave function unchanged, and that is orthogonal to the left
hand 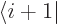 . However, in this case the interaction
Hamiltonian produces a nonzero contribution:
. However, in this case the interaction
Hamiltonian produces a nonzero contribution:
The reason is that the creation operator  acting on the right
hand ket produces a multiple
acting on the right
hand ket produces a multiple 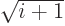 times the left hand ket.
The remaining inner product
times the left hand ket.
The remaining inner product
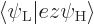 is called
the
is called
the atomic matrix element,
as it only depends on what
the atomic states are.
The task laid out in chapter 7.6.1 has been accomplished:
the relativistic matrix element has been found. A final expression
for the spontaneous emission rate can now be determined.
Before doing so, however, it is good to first compare the obtained
result with that of chapter 7.7.1. That section used a
classical given electromagnetic field, not a quantized one. So the
comparison will show up the effect of the quantization of the
electromagnetic field. The section defined a modified matrix element
This matrix element determined the entire evolution of the system.
For the quantized electric field discussed here, this coefficient
works out to be
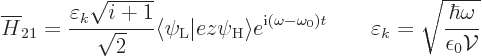 |
(A.167) |
where 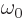

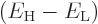

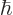 .
.
That is essentially the same form as for the classical field. Recall
that the second term in (7.44) for the classical field can
be ignored. The first term is the same as above, within a constant.
To see the real difference in the constants, note that the transition
probability is proportional to the square magnitude of the matrix
element. The square magnitudes are:
Now if there is a large number  of photons in the state, the two
expressions are approximately the same. The electromagnetic energy of
the wave according to classical physics,
of photons in the state, the two
expressions are approximately the same. The electromagnetic energy of
the wave according to classical physics,
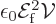
 2, {A.23}, is then
approximately the number of photons
2, {A.23}, is then
approximately the number of photons 
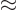
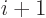 times
times
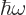 .
.
But for spontaneous emission there is a big difference. In that case,
classical physics would take the initial electromagnetic field
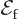 to be zero. And that then implies that the atom stays
in the excited state
to be zero. And that then implies that the atom stays
in the excited state 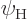 for always. There is no
electromagnetic field to move it out of the state. So there is no
spontaneous emission.
for always. There is no
electromagnetic field to move it out of the state. So there is no
spontaneous emission.
Instead quantum mechanics takes the initial field to have 
 0
photons. But note the square matrix element above. It is not zero!
The matrix element is as if there is still a full photon left in the
electromagnetic field. So spontaneous emission can and does occur in
the quantized electromagnetic field. Also, as noted in chapter
7.8, one full photon is exactly what is needed to explain
spontaneous emission. Einstein’s
0
photons. But note the square matrix element above. It is not zero!
The matrix element is as if there is still a full photon left in the
electromagnetic field. So spontaneous emission can and does occur in
the quantized electromagnetic field. Also, as noted in chapter
7.8, one full photon is exactly what is needed to explain
spontaneous emission. Einstein’s  coefficient has been found
using pure quantum analysis. Without peeking at the black body
spectrum.
coefficient has been found
using pure quantum analysis. Without peeking at the black body
spectrum.
That can also be seen without detouring through the messy analysis of
chapter 7.7 and 7.8. To find the spontaneous
emission rate directly, the matrix element above can be plugged into
Fermi’s Golden Rule (7.38) of chapter
7.6.1. The density of states needed in it was given
earlier in chapter 6.3 (6.7) and
6.19. Do note that these modes include all directions of
the electric field, not just the  -direction. To account for that,
you need to average the square atomic matrix element over all three
Cartesian directions. That produces the spontaneous transition rate
-direction. To account for that,
you need to average the square atomic matrix element over all three
Cartesian directions. That produces the spontaneous transition rate
The above result is the same as Einstein’s, (7.47) and
(7.48). (To see why a simple average works in the final
term, first note that it is obviously the right average for photons
with axial linear momenta and fields. Then note that the average is
independent of the angular orientation of the axis system in which the
photons are described. So it also works for photons that are axial in
any rotated coordinate system. To verify that the average is
independent of angular orientation does not really require linear
algebra; it suffices to show that it is true for rotation about one
axis, say the  -axis.)
-axis.)
Some additional observations may be interesting. You might think of
the spontaneous emission as caused by excitation from the ground state
electromagnetic field. But as seen earlier, the actual energy of
the ground state is half a photon, not one photon. And the zero level
of energy should not affect the dynamics anyway. According to the
analysis here, spontaneous emission is a twilight effect, chapter
5.3. The Hamiltonian coefficient 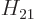 is the energy
if the atom is not excited and there is a photon if the atom is
excited and there is no photon. In quantum mechanics, the twilight
term allows the excited atom to interact with the photon that would be there if it was not excited. Sic.
is the energy
if the atom is not excited and there is a photon if the atom is
excited and there is no photon. In quantum mechanics, the twilight
term allows the excited atom to interact with the photon that would be there if it was not excited. Sic.
![]() .
.![]() .
.![]()
![]()
![]()
![]() .
.![]() -
-![]() -
-![]() -
-![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.![]() ,
,![]()
![]()
![]() -
-![]() -
-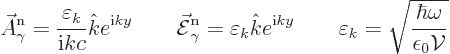
![]() :
:![]()
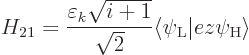
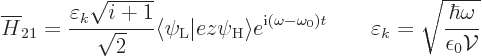
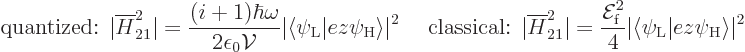
![]()
![]()
![]()
![]()
![]()
![]() -
-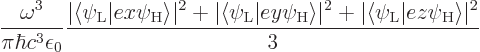
![]()