| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
7.6 Asymmetric Two-State Systems
Two-state systems are quantum systems for which just two states
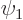 and
and 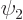 are relevant. If the two states have different
expectation energy, or if the Hamiltonian depends on time, the
two-state system is asymmetric. Such systems must be considered to
fix the problems in the description of spontaneous emission that
turned up in the previous section.
are relevant. If the two states have different
expectation energy, or if the Hamiltonian depends on time, the
two-state system is asymmetric. Such systems must be considered to
fix the problems in the description of spontaneous emission that
turned up in the previous section.
The wave function of a two state system is of the form
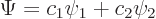 |
(7.33) |
where 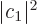 and
and  are the probabilities that the system is
in state
are the probabilities that the system is
in state 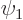 , respectively
, respectively 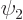 .
.
The coefficients 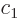 and
and 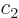 evolve in time according to
evolve in time according to
 |
(7.34) |
where
with 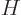 the Hamiltonian. The Hamiltonian coefficients
the Hamiltonian. The Hamiltonian coefficients
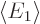 and
and 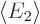 are the expectation
energies of states
are the expectation
energies of states 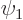 and
and 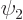 . The Hamiltonian
coefficients
. The Hamiltonian
coefficients 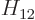 and
and 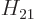 are complex conjugates. Either one
is often referred to as the
are complex conjugates. Either one
is often referred to as the matrix element.
To derive
the above evolution equations, plug the two-state wave function 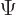 into the Schrödinger equation and take inner products with
into the Schrödinger equation and take inner products with 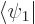 and
and  , using orthonormality of the states.
, using orthonormality of the states.
It will be assumed that the Hamiltonian is independent of time. In
that case the evolution equations can be solved analytically. To do
so, the analysis of chapter 5.3 can be used to find the
energy eigenstates and then the solution is given by the Schrödinger
equation, section 7.1.2. However, the final solution is
messy. The discussion here will restrict itself to some general
observations about it.
It will be assumed that the solution starts out in the state
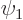 . That means that initially
. That means that initially 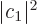
 1 and
1 and

 0. Then in the symmetric case discussed in the
previous section, the system oscillates between the two states. But
that requires that the states have the same expectation energy.
0. Then in the symmetric case discussed in the
previous section, the system oscillates between the two states. But
that requires that the states have the same expectation energy.
This section addresses the asymmetric case, in which there is a
nonzero difference  between the two expectation energies:
between the two expectation energies:
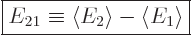 |
(7.35) |
In the asymmetric case, the system never gets into state 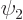 completely. There is always some probability for state
completely. There is always some probability for state 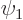 left.
That can be seen from energy conservation: the expectation value of
energy must stay the same during the evolution, and it would not if
the system went fully into state 2. However, the system will
periodically return fully to the state
left.
That can be seen from energy conservation: the expectation value of
energy must stay the same during the evolution, and it would not if
the system went fully into state 2. However, the system will
periodically return fully to the state 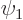 . That is all
that will be said about the exact solution here.
. That is all
that will be said about the exact solution here.
The remainder of this section will use an approximation called
“time-dependent perturbation theory.” It assumes that the
system stays close to a given state. In particular, it will be
assumed that the system starts out in state 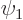 and stays close
to it.
and stays close
to it.
That assumption results in the following probability for the system to
be in the state 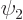 , {D.38}:
, {D.38}:
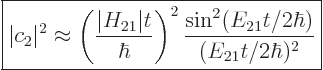 |
(7.36) |
For this expression to be a valid approximation, the parenthetical
ratio must be small. Note that the final factor shows the effect of
the asymmetry of the two state system;  is the difference in
expectation energy between the states. For a symmetric two-state
system, the final factor would be 1, (using l’Hôpital).
is the difference in
expectation energy between the states. For a symmetric two-state
system, the final factor would be 1, (using l’Hôpital).
Key Points

- If the states in a two-state system have different expectation
energies, the system is asymmetric.

- If the system is initially in the state
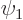 , it will
never fully get into the state
, it will
never fully get into the state 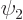 .
.

- If the system is initially in the state
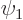 and remains
close to it, then the probability of the state
and remains
close to it, then the probability of the state 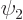 is given by
(7.36)
is given by
(7.36)
7.6.1 Spontaneous emission revisited
Decay of excited atomic or nuclear states was addressed in the
previous section using symmetric two-state systems. But there were
some issues. They can now be addressed.
The example is again an excited atomic state that transitions to a
lower energy state by emitting a photon. The state 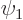 is the
excited atomic state. The state
is the
excited atomic state. The state 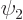 is the atomic state of
lowered energy plus the emitted photon. These states seem states of
definite energy, but if they really were, there would not be any
decay. Energy states are stationary. There is a slight uncertainty
in energy in the states.
is the atomic state of
lowered energy plus the emitted photon. These states seem states of
definite energy, but if they really were, there would not be any
decay. Energy states are stationary. There is a slight uncertainty
in energy in the states.
Since there is, clearly it does not make much sense to say that the
initial and final expectation energies must be the same
exactly.
In decay processes, a bit of energy slop  must be allowed
between the initial and final expectation values of energy.
must be allowed
between the initial and final expectation values of energy.
In practical terms, that means that the energy of the emitted photon
can vary a bit. So its frequency can vary a bit.
Now in infinite space, the possible photon frequencies are infinitely
close together. So you are now suddenly dealing with not just one
possible decay process, but infinitely many. That would require
messy, poorly justified mathematics full of so-called delta functions.
Instead, in this subsection it will be assumed that the atom is not in
infinite space, but in a very large periodic box, chapter
6.17. The decay rate in infinite space can then be found by
taking the limit that the box size becomes infinite. The advantage of
a finite box is that the photon frequencies, and so the corresponding
energies, are discrete. So you can sum over them rather than
integrate.
Each possible photon state corresponds to a different final state
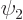 , each with its own coefficient
, each with its own coefficient 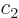 . The square
magnitude of that coefficient gives the probability that the system
can be found in that state
. The square
magnitude of that coefficient gives the probability that the system
can be found in that state 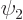 . And in the approximation
of time-dependent perturbation theory, the coefficients
. And in the approximation
of time-dependent perturbation theory, the coefficients 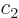 do not
interact; the square magnitude of each is given by (7.36).
The total probability that the system can be found in some
decayed state at a time
do not
interact; the square magnitude of each is given by (7.36).
The total probability that the system can be found in some
decayed state at a time 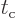 is then
is then
The time 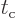 will again model the time between
will again model the time between
collisions,
interactions with the surroundings that
measure
whether the atom has decayed or not. The
decay rate, the number of transitions per unit time, is found from
dividing by the time:
The final factor in the sum for the decay rate depends on the energy
slop  . This factor is plotted graphically in figure
7.7. Notice that only a limited range around the point of
zero slop contributes much to the decay rate. The spikes in the
figure are intended to qualitatively indicate the discrete photon
frequencies that are possible in the box that the atom is in. If the
box is extremely big, then these spikes will be extremely close
together.
. This factor is plotted graphically in figure
7.7. Notice that only a limited range around the point of
zero slop contributes much to the decay rate. The spikes in the
figure are intended to qualitatively indicate the discrete photon
frequencies that are possible in the box that the atom is in. If the
box is extremely big, then these spikes will be extremely close
together.
Figure 7.7:
Energy slop diagram.
 |
Now suppose that you plot the energy slop diagram against the actual
photon energy instead of the scaled energy slop
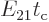

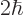 . Then the center of the diagram
will be at the nominal energy of the emitted photon and
. Then the center of the diagram
will be at the nominal energy of the emitted photon and  will
be the deviation from that nominal energy. The spike at the center
then represents the transition of atoms where the photon comes out
with exactly the nominal energy. And those surrounding spikes whose
height is not negligible represent slightly different photon energies
that have a reasonable probability of being observed. So the energy
slop diagram, plotted against photon energy, graphically represents
the uncertainty in energy of the final state that will be observed.
will
be the deviation from that nominal energy. The spike at the center
then represents the transition of atoms where the photon comes out
with exactly the nominal energy. And those surrounding spikes whose
height is not negligible represent slightly different photon energies
that have a reasonable probability of being observed. So the energy
slop diagram, plotted against photon energy, graphically represents
the uncertainty in energy of the final state that will be observed.
Normally, the observed uncertainty in energy is very small in physical
terms. The energy of the emitted photon is almost exactly the nominal
one; that allows spectral analysis to identify atoms so well. So the
entire diagram figure 7.7 is extremely narrow horizontally
when plotted against the photon energy.
Figure 7.8:
Schematized energy slop diagram.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,87...
...kebox(0,0)[b]{1}}
\put(112,18){\makebox(0,0)[b]{0}}
\end{picture}
\end{figure}](img1723.gif) |
That suggests that you can simplify things by replacing the energy
slop diagram by the schematized one of figure 7.8. This
diagram is zero if the energy slop is greater than
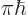

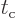 , and otherwise it is one. And it
integrates to the same value as the original function. So, if the
spikes are very closely spaced, they still sum to the same value as
before. To be sure, if the square matrix element
, and otherwise it is one. And it
integrates to the same value as the original function. So, if the
spikes are very closely spaced, they still sum to the same value as
before. To be sure, if the square matrix element  varied
nonlinearly over the typical width of the diagram, the transition rate
would now sum to something else. But it should not; if the variation
in photon energy is negligible, then so should the one in the matrix
element be.
varied
nonlinearly over the typical width of the diagram, the transition rate
would now sum to something else. But it should not; if the variation
in photon energy is negligible, then so should the one in the matrix
element be.
Using the schematized energy slop diagram, you only need to sum over
the states whose spikes are equal to 1. That are the states 2 whose
expectation energy is no more than 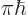

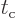 different
from the initial expectation energy. And inside this summation range,
the final factor can be dropped because it is now 1. That gives:
different
from the initial expectation energy. And inside this summation range,
the final factor can be dropped because it is now 1. That gives:
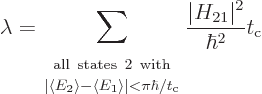 |
(7.37) |
This can be cleaned up further, assuming that 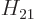 is constant and
can be taken out of the sum:
is constant and
can be taken out of the sum:
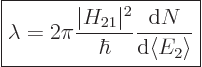 |
(7.38) |
This formula is known as “Fermi’s golden rule.” The final factor is the number of
photon states per unit energy range. It is to be evaluated at the
nominal photon energy. The formula simply observes that the number of
terms in the sum is the number of photon states per unit energy range
times the energy range. The equation is considered to originate from
Dirac, but Fermi is the one who named it “golden rule number
two.”
Actually, the original sum (7.37) may be easier to handle
in practice since the number of photon states per unit energy range is
not needed. But Fermi’s rule is important because it shows that
the big problem of the previous section with decays has been resolved.
The decay rate does no longer depend on the time between collisions
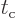 . Atoms can have specific values for their decay
rates despite the minute details of their surroundings. Shorter
collision times do produce less transitions per unit time for a given
state. But they also allow more slop in energy, so the number of
states that achieve a significant amount of transitions per unit time
goes up. The net effect is that the decay rate stays the same, though
the uncertainty in energy goes up.
. Atoms can have specific values for their decay
rates despite the minute details of their surroundings. Shorter
collision times do produce less transitions per unit time for a given
state. But they also allow more slop in energy, so the number of
states that achieve a significant amount of transitions per unit time
goes up. The net effect is that the decay rate stays the same, though
the uncertainty in energy goes up.
The other problem remains; the evaluation of the matrix element
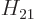 requires relativistic quantum mechanics. But it is not hard
to guess the general ideas. When the size of the periodic box that
holds the system increases, the electromagnetic field of the photons
decreases; they have the same energy in a larger volume. That results
in smaller values for the matrix element
requires relativistic quantum mechanics. But it is not hard
to guess the general ideas. When the size of the periodic box that
holds the system increases, the electromagnetic field of the photons
decreases; they have the same energy in a larger volume. That results
in smaller values for the matrix element 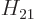 . On the other
hand, the number of photons per unit energy range
. On the other
hand, the number of photons per unit energy range
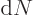

 increases, chapter
6.3. The net result will be that the decay rate remains
finite when the box becomes infinite.
increases, chapter
6.3. The net result will be that the decay rate remains
finite when the box becomes infinite.
That is verified by the relativistic analysis in addendum
{A.24}. That addendum completes the analysis in this
section by computing the matrix element using relativistic quantum
mechanics. Using a description in terms of photon states of definite
linear momentum, the matrix element is inversely proportional to the
volume of the box, but the density of states is directly proportional
to it. (It is somewhat different using a description in terms of
photon states of definite angular momentum, {A.25}.
But the idea remains the same.)
One problem of section 7.5.3 that has now disappeared is
the photon being reabsorbed again. For each individual transition
process, the interaction is too weak to produce a finite reversal
time. But quantum measurement
remains required to
explain the experiments. The time-dependent perturbation theory used
does not apply if the quantum system is allowed to evolve undisturbed
over a time long enough for a significant transition probability (to
any state) to evolve, {D.38}. That would affect the
specific decay rate. If you are merely interested in the average
emission and absorption of a large number of atoms, it is not a big
problem. Then you can substitute a classical description in terms of
random collisions for the quantum measurement process. That will be
done in derivation {D.41}. But to describe what
happens to individual atoms one at a time, while still explaining the
observed statistics of many of such individual atoms, is another
matter.
So far it has been assumed that there is only one atomic initial state
of interest and only one final state. However, either state might
have a net angular momentum quantum number  that is not zero. In
that case, there are
that is not zero. In
that case, there are 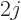 + 1 atomic states that differ only in
magnetic quantum number. The magnetic quantum number describes the
component of the angular momentum in the chosen
+ 1 atomic states that differ only in
magnetic quantum number. The magnetic quantum number describes the
component of the angular momentum in the chosen  -direction. Now if
the atom is in empty space, the direction of the
-direction. Now if
the atom is in empty space, the direction of the  -axis should not
make a difference. Then these
-axis should not
make a difference. Then these 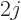 + 1 states will have the same
energy. So you cannot include one and not the other. If this happens
to the initial atomic state, you will need to average the decay rates
over the magnetic states. The physical reason is that if you have a
large number
+ 1 states will have the same
energy. So you cannot include one and not the other. If this happens
to the initial atomic state, you will need to average the decay rates
over the magnetic states. The physical reason is that if you have a
large number  of excited atoms in the given energy state, their
magnetic quantum numbers will be randomly distributed. So the average
decay rate of the total sample is the average over the initial magnetic
quantum numbers. But if it happens to the final state, you have to
sum over the final magnetic quantum numbers. Each final magnetic
quantum number gives an initial excited atom one more state that it
can decay to. The general rule is:
of excited atoms in the given energy state, their
magnetic quantum numbers will be randomly distributed. So the average
decay rate of the total sample is the average over the initial magnetic
quantum numbers. But if it happens to the final state, you have to
sum over the final magnetic quantum numbers. Each final magnetic
quantum number gives an initial excited atom one more state that it
can decay to. The general rule is:
Sum over the final atomic states, then average over the initial
atomic states.
The averaging over the initial states is typically trivial. Without a
preferred direction, the decay rate will not depend on the initial
orientation.
It is interesting to examine the limitations of the analysis in this
subsection. First, time-dependent perturbation theory has to be
valid. It might seem that the requirement of (7.36) that


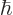 is small is automatically satisfied,
because the matrix element
is small is automatically satisfied,
because the matrix element 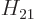 goes to zero for infinite box
size. But then the number of states 2 goes to infinity. And if you
look a bit closer at the analysis, {D.38}, the
requirement is really that there is little probability of any
transition in time interval
goes to zero for infinite box
size. But then the number of states 2 goes to infinity. And if you
look a bit closer at the analysis, {D.38}, the
requirement is really that there is little probability of any
transition in time interval 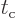 . So the time between
collisions must be small compared to the lifetime of the state. With
typical lifetimes in the range of nanoseconds, atomic collisions are
typically a few orders of magnitude more rapid. However, that depends
on the relative vacuum.
. So the time between
collisions must be small compared to the lifetime of the state. With
typical lifetimes in the range of nanoseconds, atomic collisions are
typically a few orders of magnitude more rapid. However, that depends
on the relative vacuum.
Second, the energy slop diagram figure 7.7 has to be narrow
on the scale of the photon energy. It can be seen that this is true
if the time between collisions 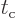 is large compared to the
inverse of the photon frequency. For emission of visible light, that
means that the collision time must be large when expressed in
femtoseconds. Collisions between atoms will easily meet that
requirement.
is large compared to the
inverse of the photon frequency. For emission of visible light, that
means that the collision time must be large when expressed in
femtoseconds. Collisions between atoms will easily meet that
requirement.
The width of the energy slop diagram figure 7.7 should give
the observed variation  in the energy of the final state. The
diagram shows that roughly
in the energy of the final state. The
diagram shows that roughly
Note that this takes the form of the all-powerful energy-time
uncertainty equality (7.9). To be sure, the equality
above involves the artificial time between collisions, or
measurements,
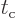 . But you could
assume that this time is comparable to the mean lifetime
. But you could
assume that this time is comparable to the mean lifetime 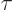 of the
state. Essentially that supposes that interactions with the
surroundings are infrequent enough that the atomic evolution can
evolve undisturbed for about the typical decay time. But that nature
will definitely commit itself whether or not a decay has occurred as
soon as there is a fairly reasonable probability that a photon has
been emitted.
of the
state. Essentially that supposes that interactions with the
surroundings are infrequent enough that the atomic evolution can
evolve undisturbed for about the typical decay time. But that nature
will definitely commit itself whether or not a decay has occurred as
soon as there is a fairly reasonable probability that a photon has
been emitted.
That argument then leads to the definition of the typical uncertainty
in energy, or width,
of a state as 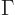

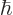

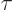 , as mentioned in section 7.4.1. In
addition, if there are frequent interactions between the atom and its
surroundings, the shorter collision time
, as mentioned in section 7.4.1. In
addition, if there are frequent interactions between the atom and its
surroundings, the shorter collision time 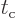 should be
expected to increase the uncertainty in energy to more than the width.
should be
expected to increase the uncertainty in energy to more than the width.
Note that the wavy nature of the energy slop diagram figure
7.7 is due to the assumption that the time between
collisions
is always the same. If you start averaging
over a more physical random set of collision times, the waves will
smooth out. The actual energy slop diagram as usually given is of the
form
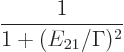 |
(7.39) |
That is commonly called a [Cauchy] “Lorentz[ian] profile” or distribution or function, or a
“Breit-Wigner distribution.” Hey, don’t blame the messenger.
In any case, it still has the same inverse quadratic decay for large
energy slop as the diagram figure 7.7. That means that if
you start computing the standard deviation in energy, you end up with
infinity. That would be a real problem for versions of the
energy-time relationship like the one of Mandelshtam and Tamm. Such
versions take the uncertainty in energy to be the standard deviation
in energy. But it is no problem for the all-powerful energy-time
uncertainty equality (7.9), because the standard deviation
in energy is not needed.
Key Points

- Some energy slop occurs in decays.

- Taking that into account, meaningful decay rates may be computed
following Fermi’s golden rule.
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,,
.
![]()
![]()
![]() ,
,![]() .
.![]() .
.![]()
![]()
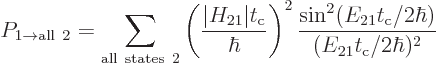
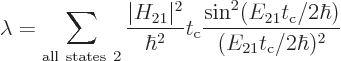
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() -
-![]() -
-![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()