|
|
|
|
|
Next: 7.6 Asymmetric Two-State Systems |
|
This section will look at the simplest quantum systems that can have nontrivial time variation. They are called symmetric two-state systems. Despite their simplicity, a lot can be learned from them.
Symmetric two-state systems were encountered before in chapter 5.3. They describe such systems as the hydrogen molecule and molecular ion, chemical bonds, and ammonia. This section will show that they can also be used as a model for the fundamental forces of nature. And for the spontaneous emission of radiation by say excited atoms or atomic nuclei.
Two-state systems are characterized by just two basic states; these
states will be called ![]()
![]() .
.
For example, for the hydrogen molecular ion ![]()
![]()
The interesting quantum mechanics arises from the fact that the two
states ![]()
![]()
![]() ,
,![]()
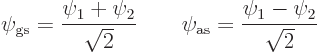
The above expressions may be inverted to give the states ![]()
![]()
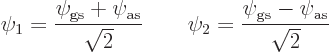
That makes their expectation energy ![]()
![]()
The question in this section is how the system evolves in time. In
general the wave function is, section 7.1,
However, this section will be more concerned with what happens to the
basic states ![]()
![]() ,
,![]()
![]()
![\begin{displaymath}
\Psi = e^{-{\rm i}\langle E \rangle t/\hbar}
\left[
c_{\r...
...rm i}\Delta E t/\hbar} \frac{\psi_1 - \psi_2}{\sqrt2}
\right]
\end{displaymath}](img1673.gif)
This expression is of the general form
The most interesting case is the one in which the system is in the
state ![]()
![]()
![]()
At time zero, the above probabilities produce state ![]()
![]() .
.![]()
![]() .
.
Key Points
- Symmetric two-state systems are described by two quantum states
and that have the same expectation energy .
- The two states have an uncertainty in energy
that is not zero.
- The probabilities of the two states are given in (7.27). This assumes that the system is initially in state
.
- The system oscillates between states
and .
Consider a simple example of the oscillatory behavior of symmetric
two-state systems. The example system is the particle inside a closed
pipe as discussed in chapter 3.5. It will be assumed that
the wave function is of the form
The above wave function is a valid solution of the Schrödinger equation since the two terms have the correct exponential dependence on time. And since the two terms have different energies, there is uncertainty in energy.
The relative probability to find the particle at a given position is
given by the square magnitude of the wave function. That works out to
The probability for finding the particle is plotted at four representative times in figure 7.6. After time (d) the evolution repeats at (a). The wave function blob is sloshing back and forth in the pipe. That is much like a classical frictionless particle with kinetic energy would bounce back and forth between the ends of the pipe.
In terms of symmetric two-state systems, you can take the state
![]()
![]()
Key Points
- A graphical example of a simple two-state system was give.
An important two-state system very similar to the simple example in the previous subsection is the hydrogen molecular ion. This ion consists of two protons and one electron.
The molecular ion can show oscillatory behavior very similar to that
of the example. In particular, assume that the electron is initially
in the ground state around the first proton, corresponding to state
![]() .
.![]() ,
,![]() .
.![]() ,
,
That may be fun, but there is something more serious that can be learned. As is, there is no (significant) force between the two protons. However, there is a second similar play-catch solution in which the electron is initially around the second proton instead of around the first. If these two solutions are symmetrically combined, the result is the ground state of the molecular ion. In this state of lowered energy, the protons are bound together. In other words, there is now a force that holds the two protons together:
If two particles play catch, it can produce forces between these two particles.
A play catch
mechanism as described above is used in
more advanced quantum mechanics to explain the forces of nature. For
example, consider the correct, relativistic, description of
electromagnetism, given by “quantum electrodynamics”. In it, the electromagnetic
interaction between two charged particles comes about largely through
processes in which one particle creates a photon that the other
particle absorbs and vice versa. Charged particles play catch using
photons.
That is much like how the protons in the molecular ion get bound together by exchanging the electron. Note however that the solution for the ion was based on the Coulomb potential. This potential implies instantaneous interaction at a distance: if, say, the first proton is moved, the electron and the other proton notice this instantaneously in the force that they experience. Classical relativity, however, does not allow effects that propagate at infinite speed. The highest possible propagation speed is the speed of light. In classical electromagnetics, charged particles do not really interact instantaneously. Instead charged particles interact with the electromagnetic field at their location. The electromagnetic field then communicates this to the other charged particles, at the speed of light. The Coulomb potential is merely a simple approximation, for cases in which the particle velocities are much less than the speed of light.
In a relativistic quantum description, the electromagnetic field is quantized into photons. (A concise introduction to this advanced topic is in addendum {A.23}.) Photons are bosons with spin 1. Similarly to classical electrodynamics, in the quantum description charged particles interact with photons at their location. They do not interact directly with other charged particles.
These are three-particle interactions, a boson and two fermions. For example, if an electron absorbs a photon, the three particles involved are the photon, the electron before the absorption, and the electron after the absorption. (Since in relativistic applications particles may be created or destroyed, a particle after an interaction should be counted separately from an identical particle that may exist before it.)
The ideas of quantum electrodynamics trace back to the early days of quantum mechanics. Unfortunately, there was the practical problem that the computations came up with infinite values. A theory that got around this problem was formulated in 1948 independently by Julian Schwinger and Sin-Itiro Tomonaga. A different theory was proposed that same year by Richard Feynman based on a more pictorial approach. Freeman Dyson showed that the two theories were in fact equivalent. Feynman, Schwinger, and Tomonaga received the Nobel prize in 1965 for this work, Dyson was not included. (The Nobel prize in physics is limited to a maximum of three recipients.)
Following the ideas of quantum electrodynamics and pioneering work by Sheldon Glashow, Steven Weinberg and Abdus Salam in 1967 independently developed a particle exchange model for the so called “weak force.” All three received the Nobel prize for that work in 1979. Gerardus ’t Hooft and Martinus Veltman received the 1999 Nobel Prize for a final formulation of this theory that allows meaningful computations.
The weak force is responsible for the beta decay of atomic nuclei,
among other things. It is of key importance for such nuclear
reactions as the hydrogen fusion that keeps our sun going. In weak
interactions, the exchanged particles are not photons, but one of
three different bosons of spin 1: the negatively charged ![]() ,
,![]() ,
,![]()
massives
because they have a nonzero rest mass, unlike
the photons of electromagnetic interactions. In fact, they have
gigantic rest masses. The ![]()
![]()
massives
is of
course completely unacceptable in physics. And neither would be
weak-force carriers,
because it is accurate and to the
point. So physicists call them the “intermediate vector bosons.” That is also three words, but
completely meaningless to most people and almost meaningless to the
rest, {A.20}. It meets the requirements of physics
well.
A typical weak interaction might involve the creation of say a
![]()
The theory of “quantum chromedynamics” describes the so-called “strong force” or “color force.” This force is responsible for such things as keeping atomic nuclei together.
The color force acts between “quarks.” Quarks are the constituents of “baryons” like the proton and the neutron, and of “mesons” like the pions. In particular, baryons consist of
three quarks, while mesons consist of a quark and an antiquark. For
example, a proton consists of two so-called up quarks
and a third down quark.
Since up quarks have electric
charge ![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,
Quarks are fermions with spin ![]()
colors
called, you guessed it, red, green and blue.
There are also three corresponding anticolors
called
cyan, magenta, and yellow.
Now the electric charge of quarks can be observed, for example in the
form of the charge of the proton. But their color charge cannot be
observed in our macroscopic world. The reason is that quarks can only
be found in colorless
combinations. In particular, in
baryons each of the three quarks takes a different color. (For
comparison, on a video screen full-blast red, green and blue produces
a colorless white.) Similarly, in antibaryons, each of the antiquarks
takes on a different anticolor. In mesons the quark takes on a color
and the antiquark the corresponding anticolor. (For example on a
video screen, if you define antigreen as magenta, i.e. full-blast red
plus blue, then green and antigreen produces again white.)
Actually, it is a bit more complicated still than that. If you had a
green and magenta flag, you might call it color-balanced, but you
would definitely not call it colorless. At least not in this book.
Similarly, a green-antigreen meson would not be colorless, and such a
meson does not exist. An actual meson is an quantum superposition of
the three possibilities red-antired, green-antigreen, and
blue-antiblue. The meson color state is
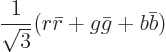
In addition, the meson color state above is a one-of-a-kind, or
“singlet” state. To see why, suppose that, say, the final
![]()
![]()
![]()
Similarly, an rgb
baryon with the first quark red, the
second green, and the third blue would be color-balanced but not
colorless. So such a baryon does not exist. For baryons there are
six different possible color combinations: there are three
possibilities for which of the three quarks is red, times two
possibilities which of the remaining two quarks is green. An actual
baryon is a quantum superposition of these six possibilities.
Moreover, the combination is antisymmetric under color exchange:
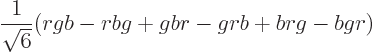
It is believed that baryons and mesons cannot be taken apart into separate quarks to study quarks in isolation. In other words, quarks are subject to “confinement” inside colorless baryons and mesons. The problem with trying to take these apart is that the force between quarks does not become zero with distance like other forces. If you try to take a quark out of a baryon or meson, presumably eventually you will put in enough energy to create a quark-antiquark pair in between. That kills off the quark separation that you thought you had achieved.
The color force between quarks is due to the exchange of so-called “gluons.” Gluons are massless bosons with spin 1 like photons. However, photons do not carry electric charge. Gluons do carry color/anticolor combinations. That is one reason that quantum chromedynamics is enormously more difficult than quantum electrodynamics. Photons cannot move electric charge from one fermion to the next. But gluons allow the interchange of colors between quarks.
Also, because photons have no charge, they do not interact with other photons. But since gluons themselves carry color, gluons do interact with other gluons. In fact, both three-gluon and four-gluon interactions are possible. In principle, this makes it conceivable that “glueballs,” colorless combinations of gluons, might exist. However, at the time of writing, 2012, only baryons, antibaryons, and mesons have been solidly established.
Gluon-gluon interactions are related to an effective strengthening of the color force at larger distances. Or as physicists prefer to say, to an effective weakening of the interactions at short distances called “asymptotic freedom.” This helps a bit because it allows some analysis to be done at very short distances, i.e. at very high energies.
Normally you would expect nine independent color/anticolor gluon states: there are three colors times three anticolors. But in fact only eight independent gluon states are believed to exist. Recall the colorless meson state described above. If a gluon could be in such a colorless state, it would not be subject to confinement. It could then be exchanged between distant protons and neutrons, giving rise to a long-range nuclear force. Since such a force is not observed, it must be concluded that gluons cannot be in the colorless state. So if the nine independent orthonormal color states are taken to be the colorless state plus eight more states orthogonal to it, then only the latter eight states can be observable. In terms of section 7.3, the relevant symmetry of the color force must be SU(3), not U(3).
Many people contributed to the theory of quantum chromedynamics.
However Murray Gell-Mann seemed to be involved in pretty much every
stage. He received the 1969 Nobel Prize at least in part for his work
on quantum chromedynamics. It is also he who came up with the name
quark.
The name is really not bad compared to many
other terms in physics. However, Gell-Mann is also responsible for
not spelling color” as “qolor.
That
would have saved countless feeble explanations that, “No, this
color has absolutely nothing to do with the color that you see in
nature.” So far nobody has been able to solve that problem, but
David Gross, David Politzer and Frank Wilczek did manage to discover
the asymptotic freedom mentioned above. For that they were awarded
the 2004 Nobel Prize in Physics.
It may be noted that Gell-Mann initially called the three colors red, white, and blue. Just like the colors of the US flag, in short. Or of the Netherlands and Taiwan, to mention a few others. Huang, [27, p. 167], born in China, with a red and yellow flag, claims red, yellow and green are now the conventional choice. He must live in a world different from ours. Sorry, but the honor of having the color-balanced, (but not colorless), flag goes to Azerbaijan.
The force of gravity is supposedly due to the exchange of particles called “gravitons.” They should be massless bosons with spin 2. However, it is hard to experiment with gravity because of its weakness on human scales. The graviton remains unconfirmed. Worse, the exact place of gravity in quantum mechanics remains very controversial.
Key Points
- The fundamental forces are due to the exchange of particles.
- The particles are photons for electromagnetism, intermediate vector bosons for the weak force, gluons for the color force, and presumably gravitons for gravity.
Symmetric two state systems provide the simplest model for spontaneous emission of radiation by atoms or atomic nuclei. The general ideas are the same whether it is an atom or nucleus, and whether the radiation is electromagnetic (like visible light) or nuclear alpha or beta radiation. But to be specific, this subsection will use the example of an excited atomic state that decays to a lower energy state by releasing a photon of electromagnetic radiation. The conservation laws applicable to this process were discussed earlier in section 7.4. This subsection wants to examine the actual mechanics of the emission process.
First, there are some important terms and concepts that must be mentioned. You will encounter them all the time in decay processes.
The big thing is that decay processes are random. A typical atom in
an excited state ![]()
![]()
Still, the decay process is not completely unpredictable. Averages
over large numbers of atoms have meaningful values. In particular,
suppose that you have a very large number ![]()
To be precise, the above decay rate is better called the specific
decay rate. The actual decay rate is usually defined to be simply
![]()
![]()
![]()
![]() .
.constant
is a term
that can mean anything, it really is still far too transparent. How
does “disintegration constant” sound? Especially since the atom
hardly disintegrates in the transition? Why not call it the
[specific] “activity,” come to think of it? Activity is another of these
vague terms. Another good one is “transition probability,” because a probability should be
nondimensional and ![]()
In fact, would it not be a good thing to take the inverse of the decay
rate? That allows another term to be defined for essentially the same
thing: the [mean] “lifetime” of the excited state:
Also, remember, if more than one decay process occurs for the excited state,
Add decay rates, not lifetimes.The sum of the decay rates gives the total decay rate of the atomic state. The reciprocal of that total is the correct lifetime.
Now suppose that initially there is a large number ![]()
![]()
![]()
A quantity with a clearer physical meaning than lifetime is the time
for about half the nuclei in a given large sample of excited atoms to
decay. This time is called the “half-life” ![]() .
.![]() :
:
The purpose in this subsection is now to understand some of the above concepts in decays using the model of a symmetric two-state system.
The initial state ![]()
![]() ,
,![]()
![]()
![]() .
.
The decayed state ![]()
![]()
![]() .
.
The probabilities of the two states were given at the start of this
section. They were:
But note that there is a problem. According to (7.32),
after another time interval ![]()
Effects like that do occur in nuclear magnetic resonance, chapter 13.6, or for atoms in strong laser light and high vacuum, [52, pp. 147-152]. But normally, decayed atoms stay decayed.
To explain that, it must be assumed that the state of the system is
measured
according to the rules of quantum mechanics,
chapter 3.4. The macroscopic surroundings
observes
that a photon is released well before the
original state can be restored. In the presence of such significant
interaction with the macroscopic surroundings, the two-state evolution
as described above is no longer valid. In fact, the macroscopic
surroundings will have become firmly committed to the fact that the
photon has been emitted. Little chance for the atom to get it back
under such conditions.
In an improved model of the transition process, section 7.6.1, the need for measurement remains. However, the reasons get more complex.
Interactions with the surroundings are generically called
collisions.
For example, a real-life atom in a gas
will periodically collide with neighboring atoms and other particles.
If a process is fast enough that no interactions with the surroundings
occur during the time interval of interest, then the process takes
place in the so-called “collisionless regime.” Nuclear magnetic resonance and atoms in
strong laser light and high vacuum may be in this regime.
However, normal atomic decays take place in the so-called “collision-dominated regime.” Here collisions with the surroundings occur almost immediately.
To model that, take the time interval between collisions to be
![]() .
.![]() .
.measured
by its surroundings and it is
either found to be in the initial excited state ![]()
![]() .
.![]()
![]()
![]() .
.
That square magnitude was given in (7.32). But it may be
approximated to:
Note that the decay process has become probabilistic. You cannot say
for sure whether the atom will be decayed or not at time
![]() .
.
However, if you have not just one excited atom, but a large number ![]()
![]()
![]() .
.![]() ,
,![]()
![]()
As mentioned earlier, the relative fraction of excited atoms that
disappears per unit time is called the decay rate ![]() .
.![]()
![]()
Physicists call ![]()
![]() ,
,
The good news is that the assumption of collisions has solved the
problem of decayed atoms undecaying again. Also, the decay process is
now probabilistic. And the decay rate ![]()
Unfortunately, there are a couple of major new problems. One problem
is that the state ![]()
![]() ;
;
An even bigger problem is that the decay rate above is proportional to
the collision time ![]() .
.
The basic problem is that in reality there is not just a single decay process for an excited atom; there are infinitely many. The derivation above assumed that the photon has an energy exactly given by the difference between the atomic states. However, there is uncertainty in energy one way or the other. Decays that produce photons whose frequency is ever so slightly different will occur too. To deal with that complication, asymmetric two-state systems must be considered. That is done in the next section.
Finally, a few words should probably be said about what collisions
really are. Darn. Typically, they are pictured as atomic collisions.
But that may be in a large part because atomic collisions are quite
well understood from classical physics. Atomic collisions do occur,
and definitely need to be taken into account, like later in the
derivations of {D.41}. But in the above description,
collisions take on a second role as doing quantum mechanical
measurements.
In that second role, a collision has
occurred if the system has been measured
to be in one
state or the other. Following the analysis of chapter 8.6,
measurement should be taken to mean that the surroundings has become
firmly committed that the system has decayed. In principle, that does
not require any actual collision with the atom; the surroundings could
simply observe that the photon is present. The bad news is that the
entire process of measurement is really not well understood at all.
In any case, the bottom line to remember is that collisions do not
necessarily represent what you would intuitively call collisions.
Their dual role is to represent the typical moment that the
surroundings commits itself that a transition has occurred.
Key Points
- The two-state system provides a model for the decay of excited atoms or nuclei.
- Interaction with the surroundings is needed to make the decay permanent. That makes decays probabilistic.
- The [specific] decay rate,
is the relative fraction of particles that decays per unit time. Its inverse is the mean lifetime of the particles. The half-life is the time it takes for half the particles in a big sample to decay. It is shorter than the mean lifetime by a factor .
- Always add decay rates, not lifetimes.