|
|
|
|
|
Next: 14. Nuclei [Unfinished Draft] |
|
Nuclear magnetic resonance, or NMR, is a valuable tool for examining nuclei, for probing the structure of molecules, in particular organic ones, and for medical diagnosis, as MRI. This section will give a basic quantum description of the idea. Linear algebra will be used.
First demonstrated independently by Bloch and Purcell in 1946, NMR
probes nuclei with net spin, in particular hydrogen nuclei or other
nuclei with spin ![]() .
.
It is not actually the spin, but the associated magnetic dipole moment of the nucleus that is relevant, for that allows the nuclei to be manipulated by magnetic fields. First the sample is placed in an extremely strong steady magnetic field. Typical fields are in terms of Tesla. (A Tesla is about 20 000 times the strength of the magnetic field of the earth.) In the field, the nucleus has two possible energy states; a ground state in which the spin component in the direction of the magnetic field is aligned with it, and an elevated energy state in which the spin is opposite {N.33}. (Despite the large field strength, the energy difference between the two states is extremely small compared to the thermal kinetic energy at room temperature. The number of nuclei in the ground state may only exceed those in the elevated energy state by say one in 100 000, but that is still a large absolute number of nuclei in a sample.)
Now perturb the nuclei with a second, much smaller and radio
frequency, magnetic field. If the radio frequency is just right, the
excess ground state nuclei can be lifted out of the lowest energy
state, absorbing energy that can be observed. The
resonance
frequency at which this happens then gives
information about the nuclei. In order to observe the resonance
frequency very accurately, the perturbing rf field must be very weak
compared to the primary steady magnetic field.
In Continuous Wave NMR, the perturbing frequency is varied and the absorption examined to find the resonance. (Alternatively, the strength of the primary magnetic field can be varied, that works out to the same thing using the appropriate formula.)
In Fourier Transform NMR, the perturbation is applied in a brief pulse just long enough to fully lift the excess nuclei out of the ground state. Then the decay back towards the original state is observed. An experienced operator can then learn a great deal about the environment of the nuclei. For example, a nucleus in a molecule will be shielded a bit from the primary magnetic field by the rest of the molecule, and that leads to an observable frequency shift. The amount of the shift gives a clue about the molecular structure at the nucleus, so information about the molecule. Additionally, neighboring nuclei can cause resonance frequencies to split into several through their magnetic fields. For example, a single neighboring perturbing nucleus will cause a resonance frequency to split into two, one for spin up of the neighboring nucleus and one for spin down. It is another clue about the molecular structure. The time for the decay back to the original state to occur is another important clue about the local conditions the nuclei are in, especially in MRI. The details are beyond this author's knowledge; the purpose here is only to look at the basic quantum mechanics behind NMR.
The magnetic fields will be assumed to be of the form
The component of the magnetic field in the ![]() -
-![]() ,
,![]() -
-![]() .
.![]()
![]()
![]() ,
,
Now suppose you place a spin ![]()
The bottom line is that you can write the Hamiltonian of the interaction
of the nucleus with the magnetic field in terms of a numerical
gyromagnetic ratio value, spin, and the magnetic field:
Now turning to the wave function of the nucleus, it can be written as
a combination of the spin-up and spin-down states,
You can use the concise notations of linear algebra by combining ![]()
![]()
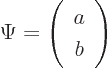
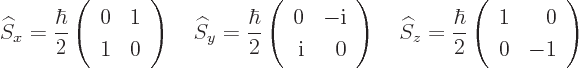 |
(13.46) |
Substitution of these expressions for the spin, and (13.44) for
the magnetic field into (13.45) gives after cleaning up the
final Hamiltonian:
Before looking at the perturbed case, it helps to first look at the
unperturbed solution. If there is just the primary magnetic field
affecting the nucleus, with no radio-frequency perturbation
![]() ,
,
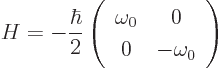
The difference in energy is in relativistic terms exactly equal to a
photon with the Larmor frequency ![]() .
.
The unsteady Schrödinger equation tells you that the wave function evolves
in time like ![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
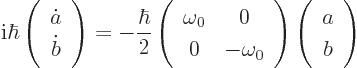
Since ![]()
![]()
![]()
![]()
![]()
![]()
But first, to understand the quantum processes better in terms of the
ideas of nonquantum physics, it will be helpful to write the
unsteady quantum evolution in terms of the expectation values of the angular momentum components. The
expectation value of the ![]() -
-
The expectation values of the angular momenta in the ![]()
![]()
![]()
![]() ,
,
The first thing that can be seen from these results is that the length
of the expectation angular momentum vector is ![]()
![]()
![]() -
-![]() .
.![]()
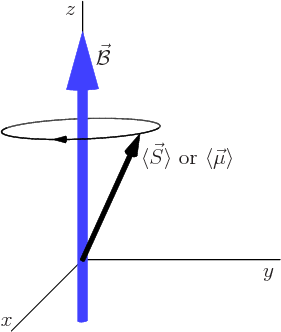 |
The component in the ![]() -
-![]() ,
,![]() -
-![]() .
.![]() -
-
Caution should be used against attaching too much importance to this
classical picture of a precessing magnet. The expectation angular
momentum vector is not a physically measurable quantity. One glaring
inconsistency in the expectation angular momentum vector versus the
true angular momentum is that the square magnitude of the expectation
angular momentum vector is ![]()
![]()
In the presence of the perturbing magnetic field, the unsteady
Schrödinger equation ![]()
![]()
![]()
The above equations can be solved exactly using standard linear
algebra procedures, though the the algebra is fairly stifling
{D.75}. The analysis brings in an additional quantity
that will be called the “resonance factor”
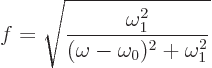 |
(13.49) |
resonance,i.e. when the perturbation frequency
The analysis finds the coefficients of the spin-up and spin-down
states to be:
![$\displaystyle \left[
a_0
\left(
\cos\bigg(\frac{\omega_1 t}{2f}\bigg)
- {\rm i}...
...f \sin\bigg(\frac{\omega_1 t}{2f}\bigg)
\right] e^{{\rm i}\omega t/2}\quad\quad$](img2996.gif) | (13.50) | ||||
![$\displaystyle \left[
b_0
\left(
\cos\bigg(\frac{\omega_1 t}{2f}\bigg)
+ {\rm i}...
... \sin\bigg(\frac{\omega_1 t}{2f}\bigg)
\right] e^{-{\rm i}\omega t/2}\quad\quad$](img2998.gif) | (13.51) |
This solution looks pretty forbidding, but it is not that bad in
application. The primary interest is in nuclei that start out in the
spin-up ground state, so you can set ![]()
![]()
![]()
![]()
| (13.52) |
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,53...
...
\put(-204,35){\makebox(0,0)[bl]{$\vert b\vert^2$}}
\end{picture}
\end{figure}](img3002.gif) |
Continuing the perturbation beyond that time is bad news; it decreases
the probability of elevated states again. As figure 13.19
shows, over extended times, there is a flip-flop between the nuclei
being with certainty in the ground state, and having a probability of
being in the elevated state. The frequency at which the probability
oscillates is called the “Rabi flopping frequency”. The author’s sources differ
about the precise definition of this frequency, but the one that seems
to be most logical is ![]()
![]()
![]() .
.
Anyway, by keeping up the perturbation for the right time you can
raise the probability of elevated energy to a maximum of ![]() .
.![]()
![]()
![]()
![]() .
.spike
in figure 13.20 must be narrow, and
since its width is proportional to ![]()
![]()
![]() ,
,
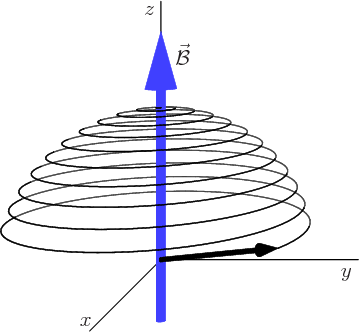 |
There are two qualitative ways to understand the need for the
frequency of the perturbation to equal the Larmor frequency. One is
geometrical and classical: as noted in the previous subsection, the
expectation magnetic moment precesses around the primary magnetic
field with the Larmor frequency. In order for the small perturbation field
to exert a long-term downward torque
on this precessing magnetic
moment as in figure 13.21, it must rotate along
with it. If it rotates at any other frequency, the torque will
quickly reverse direction compared to the magnetic moment,
and the vector will start going up again. The other way to look at it
is from a relativistic quantum perspective: if the magnetic field
frequency equals the Larmor frequency, its photons have exactly the
energy required to lift the nuclei from the ground state to the
excited state.
At the Larmor frequency, it would naively seem that the optimum time to maintain the perturbation is until the expectation spin vector is vertically down; then the nucleus is in the exited energy state with certainty. If you then allow nature the time to probe its state, every nucleus will be found to be in the excited state, and will emit a photon. (If not messed up by some collision or whatever, little in life is ideal, is it?) However, according to actual descriptions of NMR devices, it is better to stop the perturbation earlier, when the expectation spin vector has become horizontal, rather than fully down. In that case, nature will only find half the nuclei in the excited energy state after the perturbation, presumably decreasing the radiation yield by a factor 2. The classical explanation that is given is that when the (expectation) spin vector is precessing at the Larmor frequency in the horizontal plane, the radiation is most easily detected by the coils located in that same plane. And that closes this discussion.