| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.75 Solving the NMR equations
To solve the two coupled ordinary differential equations for the spin
up and down probabilities, first get rid of the time dependence of the
right-hand-side matrix by defining new variables  and
and 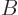 by
by
Then find the eigenvalues and eigenvectors of the now constant matrix.
The eigenvalues can be written as 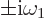

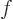 , where
, where
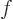 is the resonance factor given in the main text. The solution is
then
is the resonance factor given in the main text. The solution is
then
where  and
and 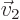 are the eigenvectors. To find the
constants
are the eigenvectors. To find the
constants  and
and  , apply the initial conditions
, apply the initial conditions 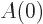

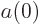

 and
and 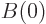

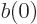

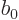 and clean
up as well as possible, using the definition of the resonance factor
and the Euler formula.
and clean
up as well as possible, using the definition of the resonance factor
and the Euler formula.
It's a mess.
![]()
![]()
![]()
![]()
![]() ,
,![]()