| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.74 Electron spin in a magnetic field
If you are curious how the magnetic dipole strength of the electron
can just pop out of the relativistic Dirac equation, this note gives a
quick derivation.
First, a problem must be addressed. Dirac's equation, chapter
12.12, assumes that Einstein's energy square root falls
apart in a linear combination of terms:
which works for the 4  4
4 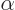 matrices given in that
section. For an electron in a magnetic field, according to chapter
13.1 you want to replace
matrices given in that
section. For an electron in a magnetic field, according to chapter
13.1 you want to replace 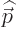 with
with 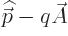 where
where
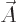 is the magnetic vector potential. But where should you do that,
in the square root or in the linear combination? It turns out that
the answer you get for the electron energy is not the same.
is the magnetic vector potential. But where should you do that,
in the square root or in the linear combination? It turns out that
the answer you get for the electron energy is not the same.
If you believe that the Dirac linear combination is the way physics
really works, and its description of spin leaves little doubt about
that, then the answer is clear: you need to put 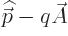 in the
linear combination, not in the square root.
in the
linear combination, not in the square root.
So, what are now the energy levels? That would be hard to say
directly from the linear form, so square it down to 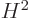 , using
the properties of the
, using
the properties of the 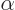 matrices, as given in chapter
12.12 and its note. You get, in index notation,
matrices, as given in chapter
12.12 and its note. You get, in index notation,
where 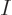 is the four by four unit matrix,
is the four by four unit matrix, 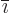 is the index
following
is the index
following  in the sequence 123123..., and
in the sequence 123123..., and 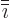 is the one
preceding
is the one
preceding  . The final sum represents the additional squared
energy that you get by substituting
. The final sum represents the additional squared
energy that you get by substituting 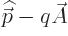 in the linear
combination instead of the square root. The commutator arises because
in the linear
combination instead of the square root. The commutator arises because
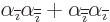
 0, giving
the terms with the indices reversed the opposite sign. Working out
the commutator using the formulae of chapter 4.5.4, and the
definition of the vector potential
0, giving
the terms with the indices reversed the opposite sign. Working out
the commutator using the formulae of chapter 4.5.4, and the
definition of the vector potential 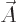 ,
,
By multiplying out the expressions for the 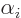 of chapter
12.12, using the fundamental commutation relation for the
Pauli spin matrices that
of chapter
12.12, using the fundamental commutation relation for the
Pauli spin matrices that 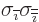

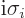 ,
,
It it seen that due to the interaction of the spin with the magnetic
field, the square energy changes by an amount
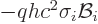 . Since
. Since 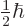 times the Pauli
spin matrices gives the spin
times the Pauli
spin matrices gives the spin 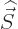 , the square energy due to the
magnetic field acting on the spin is
, the square energy due to the
magnetic field acting on the spin is 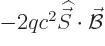 .
.
In the nonrelativistic case, the rest mass energy 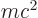 is much
larger than the other terms, and in that case, if the change in square
energy is
is much
larger than the other terms, and in that case, if the change in square
energy is 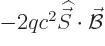 , the change in energy itself is
smaller by a factor
, the change in energy itself is
smaller by a factor 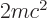 , so the energy due to the magnetic
field is
, so the energy due to the magnetic
field is
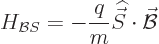 |
(D.52) |
which is what was to be proved.
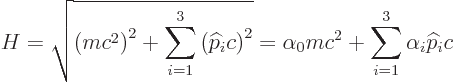
![]()
![]() ,
,![]()
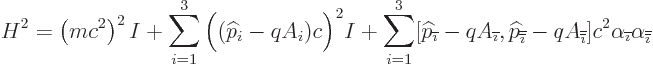
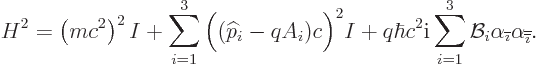
![]()
![]()
![]()
![]() ,
,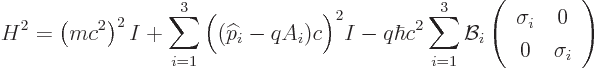
![]()
![]() ,
,![]() ,
,