| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
13.4 Particles in Magnetic Fields
Maxwell’s equations are fun, but back to real quantum mechanics.
The serious question in this section is how a magnetic field 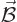 affects a quantum system, like say an electron in an hydrogen atom.
affects a quantum system, like say an electron in an hydrogen atom.
Well, if the Hamiltonian (13.2) for a charged particle
is written out and cleaned up, {D.73}, it is seen that a
constant magnetic field adds two terms. The most important of the two
is
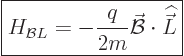 |
(13.35) |
where 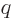 is the charge of the particle,
is the charge of the particle,  its mass,
its mass, 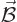 the
external magnetic field, assumed to be constant on the scale of the
atom, and
the
external magnetic field, assumed to be constant on the scale of the
atom, and  is the orbital angular momentum of the particle.
is the orbital angular momentum of the particle.
In terms of classical physics, this can be understood as follows: a
particle with angular momentum 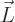 can be pictured to be
circling around the axis through
can be pictured to be
circling around the axis through 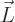 . Now according to
Maxwell’s equations, a charged particle going around in a circle
acts as a little electromagnet. Think of a version of figure
13.6 using a circular path. And a little magnet wants
to align itself with an ambient magnetic field, just like a magnetic
compass needle aligns itself with the magnetic field of earth.
. Now according to
Maxwell’s equations, a charged particle going around in a circle
acts as a little electromagnet. Think of a version of figure
13.6 using a circular path. And a little magnet wants
to align itself with an ambient magnetic field, just like a magnetic
compass needle aligns itself with the magnetic field of earth.
In electromagnetics, the effective magnetic strength of a circling
charged particle is described by the so called orbital “magnetic dipole moment” 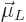 , defined as
, defined as
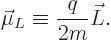 |
(13.36) |
In terms of this magnetic dipole moment, the energy is
 |
(13.37) |
which is the lowest when the magnetic dipole moment is in the same
direction as the magnetic field.
The scalar part of the magnetic dipole moment, to wit,
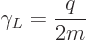 |
(13.38) |
is called the “gyromagnetic ratio.” But since in quantum mechanics the orbital
angular momentum comes in chunks of size 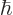 , and the
particle is usually an electron with charge
, and the
particle is usually an electron with charge 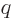


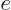 , much
of the time you will find instead the “Bohr magneton”
, much
of the time you will find instead the “Bohr magneton”
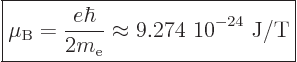 |
(13.39) |
used. Here T stands for Tesla, the kg/C-s unit of magnetic field
strength.
Please, all of this is serious; this is not a story made up by this
book to put physicists in a bad light. Note that the original formula
had four variables in it: 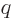 ,
,  ,
, 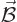 , and
, and
 , and the three new names they want you to remember are
less than that.
, and the three new names they want you to remember are
less than that.
The big question now is: since electrons have spin, build-in angular
momentum, do they still act like little magnets even if not going
around in a circle? The answer is yes; there is an additional term in
the Hamiltonian due to spin. Astonishingly, the energy involved pops
out of Dirac's relativistic description of the electron,
{D.74}. The energy that an electron picks up in a
magnetic field due to its inherent spin is:
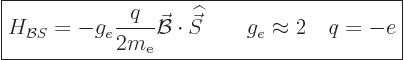 |
(13.40) |
(This section uses again 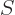 to indicate spin angular momentum.) The
constant
to indicate spin angular momentum.) The
constant 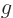 is called the “
is called the “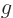 -factor”. Since its value is 2, electron spin
produces twice the magnetic dipole strength as the same amount of
orbital angular momentum would. That is called the “magnetic spin anomaly,” [52, p. 222].
-factor”. Since its value is 2, electron spin
produces twice the magnetic dipole strength as the same amount of
orbital angular momentum would. That is called the “magnetic spin anomaly,” [52, p. 222].
It should be noted that really the 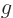 -factor of an electron is
about 0.1% larger than 2 because of the quantization of the
electromagnetic field ignored in the Dirac equation. The quantized
electromagnetic field, whose particle is the photon, has quantum
uncertainty. You can think of it qualitatively as virtual photons
popping up and disappearing continuously according to the energy-time
uncertainty
-factor of an electron is
about 0.1% larger than 2 because of the quantization of the
electromagnetic field ignored in the Dirac equation. The quantized
electromagnetic field, whose particle is the photon, has quantum
uncertainty. You can think of it qualitatively as virtual photons
popping up and disappearing continuously according to the energy-time
uncertainty 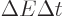
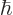 , allowing
particles with energy
, allowing
particles with energy 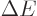 to appear as long as they don't stay
around longer than a very brief time
to appear as long as they don't stay
around longer than a very brief time 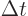 . “Quantum electrodynamics” says that to a better approximation
. “Quantum electrodynamics” says that to a better approximation
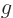
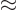
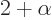

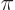 where
where 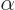

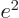

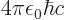
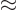 1/137 is called the fine
structure constant. This correction to
1/137 is called the fine
structure constant. This correction to 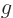 , due to the possible
interaction of the electron with a virtual photon,
[19, p. 116], is called the “anomalous magnetic moment,” [25, p. 273]. (The
fact that physicists have not yet defined potential deviations from
the quantum electrodynamics value to be “magnetic spin anomaly
anomalous magnetic moment anomalies” is an anomaly.) The
prediction of the
, due to the possible
interaction of the electron with a virtual photon,
[19, p. 116], is called the “anomalous magnetic moment,” [25, p. 273]. (The
fact that physicists have not yet defined potential deviations from
the quantum electrodynamics value to be “magnetic spin anomaly
anomalous magnetic moment anomalies” is an anomaly.) The
prediction of the 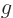 -factor of the electron is a test for the
accuracy of quantum electrodynamics, and so this
-factor of the electron is a test for the
accuracy of quantum electrodynamics, and so this 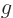 -factor has
been measured to exquisite precision. At the time of writing, (2008),
the experimental value is 2.002 319 304 362, to that many
correct digits. Quantum electrodynamics has managed to get things
right to more than ten digits by including more and more, increasingly
complex interactions with virtual photons and virtual
electron/positron pairs, [19], one of the greatest
achievements of twentieth century physics.
-factor has
been measured to exquisite precision. At the time of writing, (2008),
the experimental value is 2.002 319 304 362, to that many
correct digits. Quantum electrodynamics has managed to get things
right to more than ten digits by including more and more, increasingly
complex interactions with virtual photons and virtual
electron/positron pairs, [19], one of the greatest
achievements of twentieth century physics.
You might think that the above formula for the energy of an electron
in a magnetic field should also apply to protons and neutrons, since
they too are spin 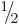 particles. However, this turns out to be
untrue. Protons and neutrons are not elementary particles, but
consist of three “quarks.” Still, for both electron and proton spin the
gyromagnetic ratio can be written as
particles. However, this turns out to be
untrue. Protons and neutrons are not elementary particles, but
consist of three “quarks.” Still, for both electron and proton spin the
gyromagnetic ratio can be written as
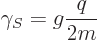 |
(13.41) |
but while the 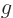 -factor of the electron is 2, the measured one for
the proton is 5.59.
-factor of the electron is 2, the measured one for
the proton is 5.59.
Do note that due to the much larger mass of the proton, its actual
magnetic dipole moment is much less than that of an electron despite
its larger 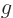 -factor. Still, under the right circumstances, like in
nuclear magnetic resonance, the magnetic dipole moment of the proton
is crucial despite its relative small size.
-factor. Still, under the right circumstances, like in
nuclear magnetic resonance, the magnetic dipole moment of the proton
is crucial despite its relative small size.
For the neutron, the charge is zero, but the magnetic moment is not,
which would make its 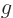 -factor infinite! The problem is that
the quarks that make up the neutron do have charge, and so the
neutron can interact with a magnetic field even though its
net charge is zero. When the proton mass and charge are
arbitrarily used in the formula, the neutron's
-factor infinite! The problem is that
the quarks that make up the neutron do have charge, and so the
neutron can interact with a magnetic field even though its
net charge is zero. When the proton mass and charge are
arbitrarily used in the formula, the neutron's 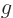 -factor is
-3.83. More generally, nuclear magnetic moments are expressed in
terms of the “nuclear magneton”
-factor is
-3.83. More generally, nuclear magnetic moments are expressed in
terms of the “nuclear magneton”
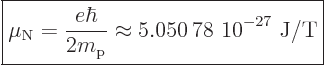 |
(13.42) |
that is based on proton charge and mass. Therefore nuclear
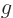 -factors are simply twice the nuclear magnetic moment in magnetons.
(Needless to say, some authors leave out the factor 2 for that
additional touch of confusion.)
-factors are simply twice the nuclear magnetic moment in magnetons.
(Needless to say, some authors leave out the factor 2 for that
additional touch of confusion.)
At the start of this subsection, it was noted that the Hamiltonian for
a charged particle has another term. So, how about it? It is called
the “diamagnetic contribution,” and it is given by
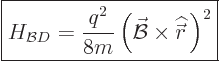 |
(13.43) |
Note that a system, like an atom, minimizes this contribution by
staying away from magnetic fields: it is positive and proportional to
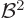 .
.
The diamagnetic contribution can usually be ignored if there is net
orbital or spin angular momentum. To see why, consider the following
numerical values:
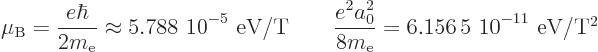
The first number gives the magnetic dipole energy, for a quantum of
angular momentum, per Tesla, while the second number gives the
diamagnetic energy, for a Bohr-radius spread around the magnetic axis,
per square Tesla.
It follows that it takes about a million Tesla for the diamagnetic
energy to become comparable to the dipole one. Now at the time of
this writing, (2008), the world record magnet that can operate
continuously is right here at the Florida State University. It
produces a field of 45 Tesla, taking in 33 MW of electricity and
4 000 gallons of cooling water per minute. The world record magnet
that can produce even stronger brief magnetic pulses is also here, and
it produces 90 Tesla, going on 100. (Still stronger magnetic fields
are possible if you allow the magnet to blow itself to smithereens
during the fraction of a second that it operates, but that is so
messy.) Obviously, these numbers are way below a million Tesla. Also
note that since atom energies are in electron volts or more, none of
these fields are going to blow an atom apart.
![]()
![]()
![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() -
-![]()
![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() -
-![]() -
-![]()
![]() -
-![]() -
-![]() -
-