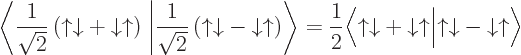5.5.6.1 So­lu­tion com­plexse-a

Ques­tion:

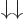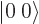Like the states ${\uparrow}{\uparrow}$, ${\uparrow}{\downarrow}$, ${\downarrow}{\uparrow}$, and ${\downarrow}{\downarrow}$; the triplet and sin­glet states are an or­tho­nor­mal quar­tet. For ex­am­ple, check that the in­ner prod­uct of ${\left\vert 1\:0\right\rangle}$ and ${\left\vert\:0\right\rangle}$ is zero.

An­swer:

By de­f­i­n­i­tion, the in­ner prod­uct is

$$\left\langle\frac 1{\sqrt 2}\left({\uparrow}{\downarrow}+ {\... ...\vert{\uparrow}{\downarrow}- {\downarrow}{\uparrow}\Big\rangle$$

and mul­ti­ply­ing out, that be­comes

$$\frac 12\left( \langle{\uparrow}{\downarrow}\vert{\uparrow}{... ...\downarrow}{\uparrow}\vert{\downarrow}{\uparrow}\rangle\right)$$

and us­ing or­tho­nor­mal­ity of the ar­row com­bi­na­tions, that is

$$\frac 12(1 - 0 + 0 - 1) = 0$$