5.5.5.1 So­lu­tion com­plexsc-a

Ques­tion:

Show that the nor­mal­iza­tion re­quire­ment for 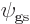$\psi_{\rm {gs}}$ means that

$$\vert a_{++}\vert^2 + \vert a_{+-}\vert^2 + \vert a_{-+}\vert^2 + \vert a_{-}\vert^2 = 1$$

An­swer:

For brevity, write

$$\psi_{{\rm gs},0} = a \left[ \psi_{\rm {l}}({\skew0\vec r}_1... ...{r}}({\skew0\vec r}_1)\psi_{\rm {l}}({\skew0\vec r}_2) \right]$$

so that

$$\psi_{\rm gs} = a_{++}\psi_{{\rm gs},0}{\uparrow}{\uparrow}+... ...w}{\uparrow}+ a_{-}\psi_{{\rm gs},0}{\downarrow}{\downarrow}.$$

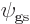For $\psi_{\rm {gs}}$ to be nor­mal­ized, its square norm must be one:

$$\langle\psi_{\rm gs}\vert\psi_{\rm gs}\rangle = 1.$$

Ac­cord­ing to the pre­vi­ous sub­sec­tion, this in­ner prod­uct eval­u­ates as the sum of the in­ner prod­ucts of the match­ing spin com­po­nents:

$$\langle a_{++}\psi_{{\rm gs},0}\vert a_{++}\psi_{{\rm gs},0}... ..._{-}\psi_{{\rm gs},0}\vert a_{-}\psi_{{\rm gs},0}\rangle = 1$$

Now the con­stants 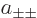$a_{\pm\pm}$ can be pulled out of the in­ner prod­ucts as 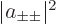$\vert a_{\pm\pm}\vert^2$, and the in­ner prod­ucts that are left, all 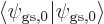$\langle\psi_{{\rm {gs}},0}\vert\psi_{{\rm {gs}},0}\rangle$, are one since 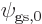$\psi_{{\rm {gs}},0}$ was nor­mal­ized through the choice of the con­stant $a$. So the claimed ex­pres­sion re­sults.