5.5.2.2 So­lu­tion com­plex­sai-b

Ques­tion:

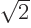As­sume that $\psi_{\rm {l}}$ and $\psi_{\rm {r}}$ are nor­mal­ized spa­tial wave func­tions. Now show that a com­bi­na­tion of the two like $\left(\psi_{\rm {l}}{\uparrow}+\psi_{\rm {r}}{\downarrow}\right)$$\raisebox{.5pt}{$/$}$​$\sqrt 2$ is a nor­mal­ized wave func­tion with spin.

An­swer:

You have

$$\left\langle\frac{\psi_{\rm {l}}{\uparrow}+\psi_{\rm {r}}{\d... ..._{\rm {l}}{\uparrow}+\psi_{\rm {r}}{\downarrow}\right\rangle ,$$

and mul­ti­ply­ing out the in­ner prod­uct ac­cord­ing to the rule spin-up com­po­nents to­gether and spin-down com­po­nents to­gether,

$$= \frac 12 \Big( \left\langle\psi_{\rm {l}}\right .\left\ver... ...i_{\rm {r}}\right .\left\vert\psi_{\rm {r}}\right\rangle\Big),$$

and since it is given that $\psi_{\rm {l}}$ and $\psi_{\rm {r}}$ are nor­mal­ized

$$= \frac 12\left(1+1\right) = 1.$$