5.5.1.1 So­lu­tion com­plexsa-a

Ques­tion:

What is the nor­mal­iza­tion re­quire­ment of the wave func­tion of a spin 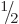$\leavevmode \kern.03em\raise.7ex\hbox{\the\scriptfont0 1}\kern-.2em /\kern-.21em\lower.56ex\hbox{\the\scriptfont0 2}\kern.05em$ par­ti­cle in terms of 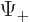$\Psi_+$ and $\Psi_-$?

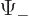An­swer:

The par­ti­cle must be found some­where, ei­ther with spin up or with spin down. The to­tal prob­a­bil­ity of find­ing it some­where with spin up is 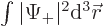$\int\vert\Psi_+\vert^2{\rm d}^3{\skew0\vec r}$, and the to­tal prob­a­bil­ity of find­ing it some­where with spin down is 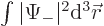$\int\vert\Psi_-\vert^2{\rm d}^3{\skew0\vec r}$. The sum of the two in­te­grals must be one to ex­press the fact that the prob­a­bil­ity of find­ing the par­ti­cle some­where, ei­ther with spin up or spin down, must be one, cer­tainty.