|
|
|
|
|
Next: 14.13 Draft: Collective Structure |
|
The liquid drop model gives a very useful description of many nuclear properties. It helps understand alpha decay quite well. Still, it has definite limitations. Quantum properties such as the stability of individual nuclei, spin, magnetic moment, and gamma decay can simply not be explained using a classical liquid model with a couple of simple fixes applied.
Historically, a major clue about a suitable quantum model came from
the magic numbers. Nuclei tend to be unusually stable if
the number of protons and/or neutrons is one of the
| (14.14) |
If an additional proton is added to a nucleus with a magic number of protons, or an additional neutron to a nucleus with a magic number of neutrons, then that additional nucleon is much more weakly bound.
The doubly magic ![]()
![]()
![]()
That is very reminiscent of the electron structure of the helium atom. The two electrons in the helium atom are very tightly bound, making helium into an inert noble gas. In fact, it takes 25 eV of energy to remove an electron from a helium atom. However, for lithium, with one more electron, the third electron is very loosely bound, and readily given up in chemical reactions. It takes only 5.4 eV to remove the third electron from lithium. Similar effects appear for the other noble gasses, neon with 10 electrons, argon with 18, krypton with 36, etcetera. The numbers 2, 10, 18, 36, ..., are magic for electrons in atoms.
For atoms, the unusual stability could be explained in chapter 5.9 by ignoring the direct interactions between electrons. It was assumed that for each electron, the complicated effects of all the other electrons could be modeled by some average potential that the electron moves in. That approximation produced single-electron energy eigenfunctions for the electrons. They then had to occupy these single-electron states one by one on account of Pauli’s exclusion principle. Noble gasses completely fill up an energy level, requiring any additional electrons to go into the next available, significantly higher energy level. That greatly decreases the binding energy of these additional electrons compared to those already there.
The similarity suggests that the protons and neutrons in nuclei might be described similarly. There are now two types of particles but in the approximation that each particle is not directly affected by the others it does not make much of a difference. Also, antisymmetrization requirements only apply when the particles are identical, either both protons or both neutrons. Therefore, protons and neutrons can be treated completely separately. Their interactions occur only indirectly through whatever is used for the average potential that they move in. The next subsections work out a model along these lines.
The first step will be to identify a suitable average potential for the nucleons. One obvious difference distinguishing nuclei from atoms is that the Coulomb potential is not going to hack it. In the electron structure of an atom the electrons repel each other, and the only reason the atom stays together is that there is a nucleus to attract the electrons. But inside a nucleus, the nucleons all attract each other and there is no additional attractive core. Indeed, a Coulomb potential like the one used for the electrons in atoms would get only the first magic number, 2, right, predicting 10, instead of 8, total particles for a filled second energy level.
A better potential is needed. Now in the center of a nucleus, the
attractive forces come from all directions and the net force will be
zero by symmetry. Away from the center, the net force will be
directed inwards towards the center to keep the nucleons together
inside the nucleus. The simplest potential that describes this is the
harmonic oscillator one. For that potential, the inward force is
simply proportional to the distance from the center. That makes the
potential energy ![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,70...
...]{\em (c)}}
\put(150,70){\makebox(0,0)[t]{\em (d)}}
\end{picture}
\end{figure}](img3144.gif) |
The energy eigenvalues of the harmonic oscillator are
spin-upstate with
(It may be noted that the above spherical eigenfunctions are different from the Cartesian ones derived in chapter 4.1, except for the ground state. However, the spherical eigenfunctions at a given energy level can be written as combinations of the Cartesian ones at that level, and vice-versa. So there is no fundamental difference between the two. It just works out that the spherical versions are much more convenient in the rest of the story.)
Compared to the Coulomb potential of the hydrogen electron as solved
in chapter 4.3, the major difference is in the number of
energy states at a given energy level ![]() .
.![]()
![]() ,
,![]()
![]()
It does not make a difference for the lowest energy level ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]() .
.
In particular, helium-4 has the lowest energy level for protons completely filled with its two protons, and the lowest level for neutrons completely filled with its two neutrons. That makes helium-4 the first doubly-magic nucleus. It is just like the two electrons in the helium atom completely fill the lowest energy level for electrons, making helium the first noble gas.
At the second energy level ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
It makes oxygen-16 with 8 protons and 8 neutrons the second
doubly-magic nucleus. Note that for the electrons in atoms, the
second energy level would also include two ![]()
![]()
Before checking the other magic numbers, first a problem with the
above procedure of counting states must be addressed. It is too easy.
Everybody can evaluate ![]()
spectroscopic notation
in which they do not tell you
the value of ![]() .
.![]()
![]()
However, physicists figured that this would not provide challenge
enough, since most students already practiced it for atoms. The above
notation follows the one that physicists use for atoms. In this
notation, the leading number is ![]() ,
,![]() ,
,official
eigenfunction designations will be listed in the final results where
appropriate. Most but not all references will follow the official
designations.
In these terms, the energy levels and numbers of states for the harmonic oscillator potential are as shown in figure 14.14. The third energy level has 2 3s states and 10 3d states. Added to the 8 from the first two energy levels, that brings the total count to 20, the third magic number.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,27...
...\tt 40?}}
\put(243,199){\makebox(0,0)[ct]{\tt 70?}}
\end{picture}
\end{figure}](img3154.gif) |
Unfortunately, this is where it stops. The fourth energy level should have only 8 states to reach the next magic number 28, but in reality the fourth harmonic oscillator level has 6 4p states and 14 4f ones. Still, getting 3 magic numbers right seems like a good start.
The logical next step is to try to improve upon the harmonic oscillator potential. In an average nucleus, it can be expected that the net force on a nucleon pretty much averages out to zero everywhere except in a very thin layer at the outer surface. The reason is that the nuclear forces are very short range; therefore the forces seem to come equally from all directions unless the nucleon is very close to the surface. Only right at the surface do the particles experience a net inward attraction because of the deficit of particles beyond the surface to provide the full compensating outward force. This suggests a picture in which the nucleons do not experience a net force within the confines of the nucleus. However, at the surface, the potential ramps up very steeply. As an idealization the potential beyond the surface can be taken infinite.
That reasoning results in the impenetrable-shell
potential shown in figure 14.13. It too is analytically
solvable, {D.77}. The energy levels are shown in
figure 14.14. Unfortunately, it does not help any
explaining the fourth magic number 28.
It does help understand why the shell model works at all, [[15]]. That is not at all obvious; for a long time physicists really believed it would not work. For the electrons in an atom, the nucleus at least produces some potential that is independent of the relative positions of the electrons. In a nucleus, there is nothing: the potential experienced by the nucleons is completely dependent on relative nucleon positions and spins. So what reasonable justification could there possibly be to assume that the nucleons act as if they move in an average potential that is independent of the other nucleons? However, first assume that the only potential energy is the one that keeps the nucleons within the experimental nuclear radius. That is the impenetrable shell model. In that case, the energy eigenfunctions are purely kinetic energy ones, and these have a shell structure. Now restore the actual complex interactions between nucleons. You would at first guess that these should greatly change the energy eigenstates. But if they really do that, it would bring in large amounts of unoccupied kinetic energy states. That would produce a significant increase in kinetic energy, and that is not possible because the binding energy is fairly small compared to the kinetic energy. In particular, therefore, removing the last nucleon should not require an energy very different from a shell model value regardless of however complex the true potential energy really is.
Of course, the impenetrable-shell potential too is open to criticism.
A nucleus has maybe ten nucleons along a diameter. Surely the
thickness of the surface layer cannot reasonably be much less than the
spacing between nucleons. Or much less than the range of the nuclear
forces, for that matter. Also, the potential should not be infinite
outside the nucleus; nucleons do escape from, or enter nuclei without
infinite energy. The truth is clearly somewhere in between the
harmonic oscillator and impenetrable shell potentials. A more
realistic potential along such lines is the “Woods-Saxon” potential
Typical energy levels are sketched in figure 14.14. As expected, they are somewhere in between the extreme cases of the harmonic oscillator and the impenetrable shell.
The signs behind the realistic energy levels in 14.14
denote the predicted “parity” of the states. Parity is a very helpful mathematical
quantity for studying nuclei. The parity of a wave function is
one,” or “positive,
or
even,
if the wave function stays the same when the
positive direction of the three Cartesian axes is inverted. That
replaces every ![]()
![]()
![]() .
.minus one,”, or “negative,
or
odd,
if the wave function merely changes sign under an
exes inversion. Parity is uncertain when the wave function changes in
any other way; however, nuclei have definite parity as long as the
weak force of beta decay does not play a role. It turns out that s,
d, g, ...states have positive parity while p, f, h, ...states
have negative parity, {D.14} or
{D.76}. Therefore, the harmonic oscillator shells
have alternatingly positive and negative parity.
For the wave functions of complete nuclei, the net parity is the product of the parities, (taking them to be one or minus one), of the individual nucleons. Now physicist can experimentally deduce the parity of nuclei in various ways. It turns out that the parities of the nuclei up to the third magic number agree perfectly with the values predicted by the energy levels of figure 14.14. (Only three unstable, artificially created, nuclei disagree.) It really appears that the model is onto something.
Unfortunately, the fourth magic number remains unexplained. In fact, any reasonable spherically symmetric spatial potential will not get the fourth magic number right. There are 6 4p states and 14 4f ones; how could the additional 8 states needed for the next magic number 28 ever be extracted from that? Twiddling with the shape of a purely spatial potential is not enough.
Eventually, Mayer in the U.S., and independently Jensen and his co-workers in Germany, concluded that spin had to be involved in explaining the magic numbers above 20. To understand why, consider the six 4p and fourteen 4f energy states at the fourth energy level of the harmonic oscillator model. Clearly, the six 4p states cannot produce the eight states of the energy shell needed to explain the next magic number 28. And neither can the fourteen 4f states, unless for some reason they split into two different groups whose energy is no longer equal.
Why would they split? In nonquantum terms, all fourteen states have orbital and spin angular momentum vectors of exactly the same lengths. What is different between states is only the direction of these vectors. And the absolute directions cannot be relevant since the physics cannot depend on the orientation of the axis system in which it is viewed. What it can depend on is the relative alignment between the orbital and spin angular momentum vectors. This relative alignment is characterized by the dot product between the two vectors.
Therefore, the logical way to get an energy splitting between states
with differently aligned orbital and spin angular momentum is to
postulate an additional contribution to the Hamiltonian of the form
spin-orbitinteraction, because it couples spin with orbital angular momentum. Spin-orbit interaction was already known from improved descriptions of the energy levels of the hydrogen atom, addendum {A.39}. However, that electromagnetic effect is far too small to explain the observed spin-orbit interaction in nuclei. Also, it would get the sign of the correction wrong for neutrons.
While nuclear forces remain incompletely understood, there is no doubt
that it is these much stronger forces, and not electromagnetic ones,
that provide the mechanism. Still, in analogy to the electronic case,
the constant of proportionality is usually taken to include the net
force ![]()
![]()
![]()
![]()
![]()
To correctly understand the effect of spin-orbit interaction on the
energy levels of nucleons is not quite trivial. Consider the fourteen
![]()
![]() -
-![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.
With spin-orbit interaction, energy eigenfunctions of nonzero orbital angular momentum no longer have definite orbital momentumTherefore the energy eigenfunctions can no longer be taken to be of the formin a chosen direction. And neither do they have definite spin -
in such a direction.
However, consider the net angular momentum operator
Now a quick review is needed of the weird way in which angular momenta
combine into net angular momentum in quantum mechanics, chapter
12.7. In classical mechanics, the sum of an angular
momentum vector with length ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
For the 4f energy level ![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
The spin-orbit interaction raises the energy of the six
4![]()
![]()
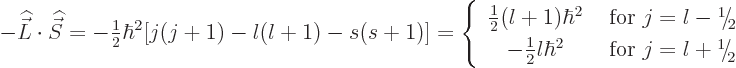
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,27...
... 70}}
\put(240,212.4){\makebox(0,0)[ct]{\tt\bf 82}}
\end{picture}
\end{figure}](img3179.gif) |
Figure 14.15 shows how the spin-orbit splitting of the
energy levels gives rise to the remaining magic numbers. In the
figure, the coefficient of the spin orbit term was simply taken to
vary linearly with the energy level ![]() .
.
The major shells, terminated by magic numbers, are shown as grey
bands. In the numbering system followed here, a subshell with a
different number as the others in the same major shell comes from a
different harmonic oscillator energy level. Figure 14.15
also shows the official
enumeration of the states.
You be the judge which numbering system makes the most sense to you.
As sketched in figure 14.15, spin-orbit interaction pushes
the 5![]()
![]()
The detailed ordering of the subshells above 50 varies with author and even for a single author. There is no unique answer, because the shell model is only a simple approximation to a system that does not follow simple rules when examined closely enough. Still, a specific ordering must be adopted if the shell model is to be compared to the data. This book will use the orderings:
The ordering for protons follows [36, table 7-1],
but not [36, p. 223], to Z=92, and then
[31], whose table seems to come from Mayer and Jensen. The
ordering for neutrons follows [36], with the
subshells beyond 136 taken from [[10]]. However, the
7![]()
![]()
![]()
![]()
The purpose of this section is to explore how the shell model works out for sample nuclei.
Figure 14.16 shows experimental energy spectra of various nuclei at the left. The energy values are in MeV. The ground state is defined to be the zero level of energy. The length and color of the energy lines indicates the spin of the nucleus, and the parity is indicated by a plus or minus sign. Some important spin values are also listed explicitly. Yellow lines indicate states for which no unique spin and/or parity are determined or are established with reservations. At the right in the figure, a sketch of the occupation levels according to the shell model is displayed for easy reference.
The top of the figure shows data for oxygen-16, the normal oxygen that makes up 99.8% of the oxygen in the atmosphere. Oxygen-16 is a doubly-magic nucleus with 8 protons and 8 neutrons. As the right-hand diagram indicates, these completely fill up the lowest two major shells.
As the left-hand spectrum shows, the oxygen-16 nucleus has zero net spin in the ground state. That is exactly what the shell model predicts. In fact, it is a consequence of quantum mechanics that:
Completely filled subshells have zero net angular momentum.Since the shell model says all shells are filled, the zero spin follows. The shell model got the first one right. Indeed, it passes this test with flying colors for all doubly-magic nuclei.
Next,
Subshells with an even number of nucleons have even parity.That is just a consequence of the fact that even if the subshell is a negative parity one, negative parities multiply out pairwise to positive ones. Since all subshells of oxygen-16 contain an even number of nucleons, the combined parity of the complete oxygen-16 nucleus should be positive. It is. And it is for the other doubly-magic nuclei.
The shell model implies that a doubly-magic nucleus like oxygen-16 should be be particularly stable. So it should require a great deal of energy to excite it. Indeed it does: figure 14.16 shows that exciting oxygen-16 takes over 6 MeV of energy.
Following the shell model picture, one obvious way to excite the
nucleus would be to kick a single proton or neutron out of the
2![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Still, the exited ![]()
Next consider oxygen-17 and fluorine-17 in figure 14.16.
These two are examples of so-called mirror nuclei;
they have the numbers of protons and neutrons reversed. Oxygen-17 has
8 protons and 9 neutrons while its twin fluorine-17 has 9 protons and
8 neutrons. The similarity in energy levels between the two
illustrates the idea of charge symmetry: nuclear forces are the same if the protons are turned
into neutrons and vice versa. (Of course, this swap does mess up the
Coulomb forces, but Coulomb forces are not very important for light
nuclei.)
Each of these two nuclei has one more nucleon in addition to an
oxygen-16 core
. Since the filled subshells of the
oxygen-16 core have zero spin, the net nuclear spin should be that of
the odd nucleon in the 3![]()
This is a big test for the shell model, because if a doubly-magic-plus-one nucleus did not have the predicted spin and parity of the final odd nucleon, there would be no reasonable way to explain it. Fortunately, all nuclei of this type pass the test.
For both oxygen-17 and fluorine-17, there is also a low-energy ![]()
![]()
![]()
![]()
However, from the shell model, in particular figure 14.15,
you would expect the spacing between the 3![]()
![]()
![]()
![]()
Then there are the odd parity states. These are not so easy to
understand: they require a nucleon to be kicked up past a major shell
boundary. That should require a lot of energy according to the ideas
of the shell model. It seems to make them hard to reconcile with the
much higher energy of the ![]()
The fourth nucleus in figure 14.16 is nitrogen-14. This
is an odd-odd nucleus, with both an odd number of protons and of
neutrons. The odd proton and odd neutron are in the 2![]()
![]() .
.![]()
![]()
The most obvious way to further excite the nucleus with minimal energy
would be to kick up a nucleon from the 2![]()
![]()
![]()
![]()
Holes in an otherwise filled subshell have the same possible angular momentum values as particles in an otherwise empty shell.Therefore the hole must have the spin
The next higher ![]()
![]()
![]()
![]()
![]()
This section examines some nuclei with more than a single nucleon in an unfilled shell.
Consider first oxygen-18 in figure 14.17, with both an
even number of protons and an even number of neutrons. As always, the
filled subshells have no angular momentum. That leaves the two
3![]()
Now the basic shell model is an “independent particle model:” there are no direct interactions between the particles. Each particle moves in a given average potential, regardless of what the others are doing. Therefore, if the shell model as covered so far would be strictly true, all three spin states 0, 2, and 4 of oxygen-18 should have equal energy. Then the ground state should be any combination of these spins. But that is untrue. The ground-state has zero spin:
All even-even nuclei have zero spin and even parity in the ground state.There are zero known exceptions to this rule among either the stable or unstable nuclei.
So physicists have concluded that besides the average potential
included in the shell model, there must be an additional
pairing energy
that makes nucleons of the same type
want to combine pairwise into states of zero spin. In order to treat
this effect mathematically without losing the basic shell model, the
pairing energy must be treated as a relatively small perturbation to
the shell model energy. Theories that do so are beyond the scope of
this book, although the general ideas of perturbation theories can be
found in addendum {A.38}. Here it must be suffice to note
that the pairing effect exists and is due to interactions between
nucleons not included in the basic shell model potential.
Therefore the basic shell model will from here on be referred to as the “unperturbed” shell model. The “perturbed shell model” will refer to the shell model in which additional energy corrections are assumed to exist that account for nontrivial interactions between individual nucleons. These corrections will not be explicitly discussed, but some of their effects will be demonstrated by means of experimental energy spectra.
If the pairing energy is a relatively small perturbation to the shell
model, then for oxygen-18 you would expect that besides the zero spin
ground state, the other possibilities of spin 2 and 4 would show up as
low-lying excited states. Indeed the experimental spectrum in figure
14.17 shows ![]()
![]()
![]()
![]()
If one neutron of the pair is kicked up to the 3![]()
![]()
![]()
![]()
Like for oxygen-16, there is again an excited ![]()
![]()
![]()
The pairing energy increases with the angular momentum of the subshell.When the neutron pair is kicked from the 3
It seems therefore that the perturbed shell model can give a plausible explanation for the various features of the energy spectrum. However, care must be taken not to attach too much finality to such explanations. Section 14.13 will give a very different take on the excited states of oxygen-18. Presumably, neither explanation will be very accurate. Only additional considerations beyond mere energy levels can decide which explanation gives the better description of the excited states.
The purpose in this section is to examine what features seem to have a reasonable explanation within a shell model context, not how absolutely accurate that explanation really is.
Consider again the ![]()
![]()
![]()
![]()
Similarly, the relatively low energy ![]()
![]()
![]()
So what to make of the next ![]()
![]()
![]()
![]()
![]()
![]()
![]()
How about nuclei with an odd number of neutrons and/or protons in a subshell that is greater than one? For these:
TheThat leaves only the final odd nucleon to provide any nonzero spin and corresponding nontrivial electromagnetic properties.odd-particle shell modelpredicts that even if the number of nucleons in a subshell is odd, in the ground state all nucleons except the final odd one still combine into spherically symmetric states of zero spin.
Figure 14.17 shows the example of oxygen-19, with three
neutrons in the unfilled 3![]()
It is important to recognize that the odd-particle shell model only
applies to the ground state. This is not always sufficiently
stressed. Theoretically, three 3![]()
![]()
![]()
It is also important to recognize that the odd-particle shell model is
only a prediction. It does fail for a fair number of nuclei. That is
true even excluding the very heavy nuclei for which the shell model
does not apply period. For example, note in figure
14.17 how close together are the ![]()
![]()
It should be noted that different terms are used in literature for the
odd-particle shell model. The term “shell model with
pairing” is accurate and understandable, so that is not used.
Some authors use the term “extreme independent particle model.” You read that right.
While the unperturbed shell model is an independent particle model,
the shell model with pairing has become a dependent particle
model: there are now postulated direct interactions between the
nucleons causing them to pair. So what better way to confuse students
than to call a dependent particle model an extreme
independent particle model? However, this term is too blatantly
wrong even for some physicists. So, some other books use instead
“extreme single-particle model,” and still others use “one-particle shell model.” Unfortunately, it is fundamentally a
multiple-particle model. You cannot have particle interactions with a
single particle. Only physicists would come up with three different
names for the same model and get it wrong in each single case. This
book uses the term odd-particle shell model, (with odd in dictionary
rather than mathematical sense), since it is not wrong and sounds much
like the other names being bandied around. (The official names could
be fixed up by adding the word almost,
like in
extreme almost independent particle model.
This book
will not go there, but you could substitute
asymptotically” for “almost
to sound
more scientific.)
While the odd-particle model applies only to the ground state,
some excited states can still be described as purely
odd-particle effects. In particular, for the oxygen-19 example, the
odd 3![]()
![]()
![]()
![]()
![]()
It may further be noted that pairing
is not really the
right quantum term. If two nucleons have paired into the combination
of zero net spin, the next two cannot just enter the same combination
without violating the antisymmetrization requirements between the
pairs. What really happens is that all four as a group combine into a
state of zero spin. However, everyone uses the term pairing, and so
will this book.
Examples that highlight the perturbation effects of the shell model
are shown in figure 14.18. These nuclei have unfilled
4![]()
First observe that all three nuclei have a final odd 4![]()
As far as calcium-41 is concerned, one obvious minimal-energy
excitation would be that the odd neutron is kicked up from the
4![]()
![]()
![]()
Another obvious minimal-energy excitation would be that a nucleon is
kicked up from the filled 3![]()
![]()
![]()
![]()
![]()
The unstable mirror twin of calcium-41, scandium-41 has energy levels that are very much the same.
Next consider calcium-43. The odd-particle shell model correctly
predicts that in the ground state, the first two 4![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The lowest ![]()
![]()
![]()
Scandium-43 has one proton and two neutrons in the 4![]()
![]()
![]() .
.![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
Note how low the lowest ![]()
![]()
The difference between the energy levels of scandium-41 versus
scandium-43 is dramatic. After all, the unperturbed shell model would
almost completely ignore the two additional neutrons that scandium-43
has. Protons and neutrons are solved for independently in the model.
It brings up a point that is often not sufficiently emphasized in
other expositions of nuclear physics. The odd-particle shell model is
not an only the last odd particle is important
model. It is a “the last odd particle provides the ground-state
spin and electromagnetic properties, because the other particles are
paired up in spherically symmetric states” model. The
theoretical justification for the model, which is weak enough as it is
already, only applies to the second statement.
To better understand the shell model and its limitations, combinations of states must be considered.
Take once again the excited ![]()
![]()
![]()
First of all, there are two ways to do it: either the
2![]()
![]()
![]()
![]() .
.
Quantum mechanics allows for linear combinations of the two wave
functions:
But now consider the possibility that both the protons and the
neutrons would be in the 3![]()
Of course, the four nucleons are not all in the
3![]()
![]()
twilight
terms, chapter 5.3. These act
in some sense as if all four nucleons are indeed in the
3![]()
![]()
![]()
The amount of energy lowering is hard to predict. It depends on the
amount of nucleon positions that have a reasonable probability for
both states and the amount of interaction of the nucleons. Intuition
still suggests it should be quite considerable. And there is a more
solid argument. If the strictly unperturbed shell model applies,
there should be two ![]()
![]()
Of course, a weird excited state at 6 MeV in a nucleus is not such a
big deal. But there is more. Consider figure 14.19. It
gives the excitation energy of the lowest ![]()
For all nuclei except the crossed-out ones, the ![]()
![]()
![]()
The alternative way to excite an even-even nucleus with minimal energy
would break up a pair, but leave them in the same subshell. This
would at the minimum create a ![]()
![]()
Then there is the magnitude of the ![]()
But for nuclei that are not close to any magic number for either protons and neutrons all hell breaks loose. Break-up energies one to two orders of magnitude less than the von Weizsäcker value are common. How can the pairing energy just suddenly stop to exist?
Consider a couple of examples in figure 14.20. In
case of ruthenium-104, it takes a measly 0.36 MeV to excite the ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Consider now the following simplistic model. Assume that the nucleus
can be in any of ![]()
To get an idea of what can happen, assume for now that the
![]()
![]()
![]() .
.![]()
![]()
Of course, the coefficients ![]()
The picture that emerges then is that the ![]()
![]()
![]()
![]()
When the energy of the excitation hits zero, the bottom quite
literally drops out of the shell model. In fact, even if the energy
merely becomes low, the shell model must crash. If energy states are
almost degenerate, the slightest thing will throw the nucleus from one
to the other. In particular, small perturbation theory shows that
originally small effects blow up as the reciprocal of the energy
difference, addendum {A.38}. Physicists have found that
nuclei in the rough ranges 150 ![]()
![]()
![]()
![]()
![]()
The previous subsection already indicated two cases in which the shell model has major problems with the excited states. But in a number of cases the shell model may also predict an incorrect ground state. Figure 14.21 shows some typical examples.
In case of titanium-47, the shell model predicts that there will be
five neutrons in an unfilled 4![]()
![]() .
.![]() .
.![]()
In fact, 5 particles in a shell in which the single-particle spin is
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
Fluorine-19 shows a more fundamental failure of the shell model. The
shell model would predict that the odd proton is in the
3![]()
![]()
![]() ,
,![]()
It is the theoretician’s loss, but the experimentalist’s gain. The fact that fluorine has spin one-half makes it a popular target for nuclear magnetic resonance studies. Spin one-half nuclei are easy to analyze and they do not have nontrivial electric fields that mess up the nice sharp signals in nuclei with larger spin.
And maybe the theoretician can take some comfort in the fact that this complete failure is rare among the light nuclei. In fact, the main other example is fluorine-19’s mirror twin neon-19. Also, there is an excited state with the correct spin and parity just above the ground state. But no funny business here; if you are going to call fluorine-19 almost right, you have to call fluorine-17 almost wrong.
Note also how low the ![]()
![]()
And note that formulating a perturbed shell model from physical principles is not easy anyway, because the basic shell model already includes the interactions between nucleons in an average sense. The perturbations must not just identify the interactions, but more importantly, what part of these interactions is still missing from the unperturbed shell model.
For the highly unstable beryllium-11 and nitrogen-11 mirror nuclei,
the shell model gets the spin right, but the parity wrong! In shell
model terms, a change of parity requires the crossing of a major shell
boundary. Beryllium-11 is known to be a “halo nucleus,” a nucleus whose radius is noticeably larger than
that predicted by the liquid drop formula (14.9). This is
associated with a gross inequality between the number of protons and
neutrons. Beryllium-11 has only 4 protons, but 7 neutrons; far too
many for such a light nucleus. Beryllium-13 with 9 neutrons
presumably starts to simply throw the bums out. Beryllium-11 does not
do that, but it keeps one neutron at arms length. The halo of
beryllium-11 is a single neutron one. (That of its beta-decay parent
lithium-11 is a two-neutron one. Such a nucleus is called “Borromean,” after the three interlocking rings in the shield of
the princes of Borromeo. Like the rings, the three-body system
lithium-9 plus two neutrons hangs together but if any of the three is
removed, the other two fall apart too. Both lithium-10 and the
dineutron are not bound.) Halo nucleons tend to prefer states of low
orbital angular momentum, because in classical terms it reduces the
kinetic energy they need for angular motion. The potential energy is
less significant so far out. In shell model terms, the beryllium-11
neutron has the 3![]()
![]()
![]()
For much heavier nuclei, the subshells are often very close together.
Also, unlike for the 3![]()
![]()
Selenium-77 illustrates a more fundamental reason why the odd particle
may end up in the wrong state. The final odd neutron would normally
be the third one in the 5![]()
![]()
![]()
![]()
![]()
![]()
![]()
Tantalum-181 is an example nucleus that is not spherical. For it, the
shell model simply does not apply as derived here. So there is no
need to worry about it. Which is a good thing, because it does not
seem easy to justify a ![]()
Preston & Bhaduri [36, p. 224ff] give an
extensive table of nucleons with odd mass number, listing shell
occupation numbers and spin. Notable is iron-57, believed to have
three neutrons in the 4![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()