| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
14.11 Draft: Alpha Decay
In alpha decay a nucleus emits an “alpha particle,” later identified to be simply a helium-4
nucleus. Since the escaping alpha particle consists of two protons
plus two neutrons, the atomic number 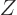 of the nucleus decreases by
two and the mass number
of the nucleus decreases by
two and the mass number  by four. This section explains why alpha
decay occurs.
by four. This section explains why alpha
decay occurs.
14.11.1 Draft: Decay mechanism
Figure 14.10 gives decay data for the nuclei that decay
exclusively through alpha decay. Nuclei are much like cherries: they
have a variable size that depends mainly on their mass number
 , and a charge
, and a charge 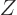 that can be shown as different shades of
red. You can even define a
that can be shown as different shades of
red. You can even define a stem
for them, as
explained later. Nuclei with the same atomic number 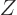 are joined by
branches.
are joined by
branches.
Figure 14.10:
Half-life versus energy release for the atomic nuclei
marked in NUBASE 2003 as showing pure alpha decay with
unqualified energies. Top: only the even values of the mass and
atomic numbers cherry-picked, omitting
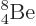 . Inset: really cherry-picking,
only a few even mass numbers for thorium and uranium! Bottom:
all the nuclei except
. Inset: really cherry-picking,
only a few even mass numbers for thorium and uranium! Bottom:
all the nuclei except 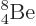 (67 as,
0.092 MeV).
[pdf]
(67 as,
0.092 MeV).
[pdf]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,37...
...ebox(0,0)[b]{5}}
\put(-66,210){\makebox(0,0)[b]{6}}
\end{picture}
\end{figure}](img3114.gif) |
Not shown in figure 14.10 is the unstable beryllium
isotope 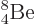 , which has a half-life of only
67 as, (i.e. 67 10
, which has a half-life of only
67 as, (i.e. 67 10 s), and a decay energy of only 0.092 MeV. As
you can see from the graph, these numbers are wildly different from
the other, much heavier, alpha-decay nuclei, and inclusion would make
the graph very messy.
s), and a decay energy of only 0.092 MeV. As
you can see from the graph, these numbers are wildly different from
the other, much heavier, alpha-decay nuclei, and inclusion would make
the graph very messy.
Note the tremendous range of half-lives in figure 14.10,
from mere nanoseconds to quintillions of years. And that excludes
beryllium’s attoseconds. In the early history of alpha decay, it
seemed very hard to explain how nuclei that do not seem that different
with respect to their numbers of protons and neutrons could have such
dramatically different half-lives. The energy that is released in the
decay process does not vary that much, as figure 14.10
also shows.
To add to the mystery in those early days of quantum mechanics, if an
alpha particle was shot back at the nucleus with the same energy that
it came out, it would not go back in! It was reflected by the
electrostatic repulsion of the positively charged nucleus. So, it
had not enough energy to pass through the region of high potential
energy surrounding the nucleus, yet it did pass through it when
it came out.
Gamow, and independently Gurney & Condon, recognized that the
explanation was quantum tunneling. Tunneling allows a particle to get
through a potential energy barrier even if classically it does not
have enough energy to do so, chapter 7.12.2.
Figure 14.11:
Schematic potential for an alpha particle that tunnels
out of a nucleus.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,13...
...}
\put(-86,64){\makebox(0,0)[r]{$V_{\rm Coulomb}$}}
\end{picture}
\end{figure}](img3115.gif) |
Figure 14.11 gives a rough model of the barrier.The
horizontal line represents the total energy of the alpha particle.
Far from the nucleus, the potential energy 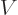 of the alpha particle
can be defined to be zero. Closer to the nucleus, the potential
energy of the alpha particle ramps up due to Coulomb repulsion.
However, right at the outer edge
of the alpha particle
can be defined to be zero. Closer to the nucleus, the potential
energy of the alpha particle ramps up due to Coulomb repulsion.
However, right at the outer edge 

 of the nucleus itself,
the strong but very short-range attractive nuclear force pops up, and
the combined potential energy plummets almost vertically downwards to
some low value
of the nucleus itself,
the strong but very short-range attractive nuclear force pops up, and
the combined potential energy plummets almost vertically downwards to
some low value 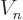 . In between the radial position
. In between the radial position 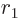
 and some larger radius
and some larger radius  , the potential energy
exceeds the total energy that the alpha particle has available.
Classically, the alpha particle cannot penetrate into this region.
However, in quantum mechanics it retains a very small probability of
doing so.
, the potential energy
exceeds the total energy that the alpha particle has available.
Classically, the alpha particle cannot penetrate into this region.
However, in quantum mechanics it retains a very small probability of
doing so.
The region in between 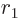 and
and 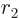 is called the “Coulomb barrier.” It is a poorly chosen name, because the
barrier is only a Coulomb one for an alpha particle trying to get
in the nucleus. For an alpha particle trying to get
out, it is a nuclear force barrier; here the Coulomb force
assists the tunneling particle to get through the barrier and escape.
The term
is called the “Coulomb barrier.” It is a poorly chosen name, because the
barrier is only a Coulomb one for an alpha particle trying to get
in the nucleus. For an alpha particle trying to get
out, it is a nuclear force barrier; here the Coulomb force
assists the tunneling particle to get through the barrier and escape.
The term nuclear barrier
would avoid this ambiguity.
Therefore physicists do not use it.
Now, to get a rough picture of alpha decay, imagine an alpha particle
wave packet rattling around
inside the nucleus trying
to escape. Each time it hits the barrier at 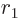 , it has a
small chance of escaping. Eventually it gets lucky.
, it has a
small chance of escaping. Eventually it gets lucky.
Assume that the alpha particle wave packet is small enough that the
motion can be assumed to be one-dimensional. Then the small chance of
escaping each time it hits the barrier is approximately given by the
analysis of chapter 7.13 as
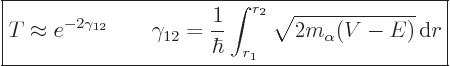 |
(14.12) |
The fact that this probability involves an exponential is the basic
reason for the tremendous range in half-lives: exponentials can vary
greatly in magnitude for relatively modest changes in their argument.
14.11.2 Draft: Comparison with data
The previous subsection explained alpha decay in terms of an
imprisoned alpha particle tunneling out of the nucleus. To verify
whether that is reasonable, the next step is obviously to put in some
ballpark numbers and see whether the experimental data can be
explained.
First, the energy  of the alpha particle may be found from
Einstein’s famous expression
of the alpha particle may be found from
Einstein’s famous expression 

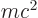 , section
14.6. Just find the difference between the rest mass of the
original nucleus and the sum of that of the final nucleus and the
alpha particle, and multiply by the square speed of light. That gives
the energy release. It comes out primarily as kinetic energy of the
alpha particle, ignoring any excitation energy of the final nucleus.
(A reduced mass can be used to allow for recoil of the nucleus.) Note
that alpha decay cannot occur if
, section
14.6. Just find the difference between the rest mass of the
original nucleus and the sum of that of the final nucleus and the
alpha particle, and multiply by the square speed of light. That gives
the energy release. It comes out primarily as kinetic energy of the
alpha particle, ignoring any excitation energy of the final nucleus.
(A reduced mass can be used to allow for recoil of the nucleus.) Note
that alpha decay cannot occur if  is negative; the kinetic energy
of the alpha particle cannot be negative.
is negative; the kinetic energy
of the alpha particle cannot be negative.
It may be noted that the energy release  in a nuclear process is
generally called the “
in a nuclear process is
generally called the “ -value.” The reason is that one of the most common
other quantities used in nuclear physics is the so-called quadrupole
moment
-value.” The reason is that one of the most common
other quantities used in nuclear physics is the so-called quadrupole
moment  . Also, the total nuclear charge is indicated by
. Also, the total nuclear charge is indicated by
 , as is the quality factor of radiation, while projection and
rotation operators, and second points are often also indicted by
, as is the quality factor of radiation, while projection and
rotation operators, and second points are often also indicted by
 . The underlying idea is that when you are trying to figure
out some technical explanation, then if almost the only mathematical
symbol used is
. The underlying idea is that when you are trying to figure
out some technical explanation, then if almost the only mathematical
symbol used is  , it provides a pretty strong hint that you
are probably reading a book on nuclear physics.
, it provides a pretty strong hint that you
are probably reading a book on nuclear physics.
The nuclear radius  approximately defines the start
approximately defines the start 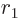 of the
region that the alpha particle has to tunnel through, figure
14.11. It can be ballparked reasonably well from the
number of nucleons
of the
region that the alpha particle has to tunnel through, figure
14.11. It can be ballparked reasonably well from the
number of nucleons  ; according to section 14.10,
; according to section 14.10,
where f, femto, is 10 . That is a lot smaller than the typical
Bohr radius over which electrons are spread out. Electrons are
. That is a lot smaller than the typical
Bohr radius over which electrons are spread out. Electrons are
far away
and are not really relevant.
It should be pointed out that the results are very sensitive to the
assumed value of 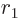 . The simplest assumption would be that
at
. The simplest assumption would be that
at 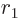 the alpha particle would have its center at the nuclear
radius of the remaining nucleus, computed from the above expression.
But very noticeable improvements are obtained by assuming that at
the alpha particle would have its center at the nuclear
radius of the remaining nucleus, computed from the above expression.
But very noticeable improvements are obtained by assuming that at
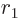 the center is already half the radius of the alpha particle
outside. (In literature, it is often assumed that the alpha particle
is a full radius outside, which means fully outside but still touching
the remaining nucleus. However, half works better and is maybe
somewhat less implausible.)
the center is already half the radius of the alpha particle
outside. (In literature, it is often assumed that the alpha particle
is a full radius outside, which means fully outside but still touching
the remaining nucleus. However, half works better and is maybe
somewhat less implausible.)
The good news about the sensitivity of the results on 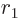 is that
conversely it makes alpha decay a reasonably accurate way to deduce or
verify nuclear radii, [31, p. 57]. You are hardly likely to
get the nuclear radius noticeably wrong without getting into major
trouble explaining alpha decay.
is that
conversely it makes alpha decay a reasonably accurate way to deduce or
verify nuclear radii, [31, p. 57]. You are hardly likely to
get the nuclear radius noticeably wrong without getting into major
trouble explaining alpha decay.
The number of escape attempts per unit time is also needed. If the
alpha particle has a typical velocity 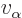 inside the original
nucleus, it will take it a time of about
inside the original
nucleus, it will take it a time of about 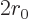

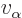 to travel
the
to travel
the 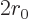 diameter of the nucleus. So it will bounce against the
barrier about
diameter of the nucleus. So it will bounce against the
barrier about 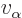

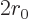 times per second. That is sure to be
a very large number of times per second, the nucleus being so small,
but each time it hits the perimeter, it only has a miniscule
times per second. That is sure to be
a very large number of times per second, the nucleus being so small,
but each time it hits the perimeter, it only has a miniscule
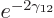 chance of escaping. So it may well take trillions
of years before it is successful anyway. Even so, among a very large
number of nuclei a few will get out every time. Remember that a mol
of atoms represents in the order of 10
chance of escaping. So it may well take trillions
of years before it is successful anyway. Even so, among a very large
number of nuclei a few will get out every time. Remember that a mol
of atoms represents in the order of 10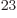 nuclei; among that
many nuclei, a few alpha particles are likely to succeed whatever the
odds against. The relative fraction of successful escape attempts per
unit time is by definition the reciprocal of the lifetime
nuclei; among that
many nuclei, a few alpha particles are likely to succeed whatever the
odds against. The relative fraction of successful escape attempts per
unit time is by definition the reciprocal of the lifetime
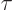 ;
;
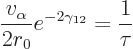 |
(14.13) |
Multiply the lifetime by 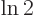 to get the half-life.
to get the half-life.
The velocity 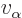 of the alpha particle can be ballparked from
its kinetic energy
of the alpha particle can be ballparked from
its kinetic energy 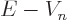 in the nucleus as
in the nucleus as
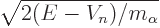 . Unfortunately, finding an accurate
value for the nuclear potential
. Unfortunately, finding an accurate
value for the nuclear potential 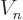 inside the nucleus is not
trivial. But have another look at figure 14.10. Forget
about engineering ideas about acceptable accuracy. A 50% error in
half-life would be invisible seen on the tremendous range of figure
14.10. Being wrong by a factor 10, or even a factor
100, two orders of magnitude, is ho-hum on the scale that the
half-life varies. So, the potential energy
inside the nucleus is not
trivial. But have another look at figure 14.10. Forget
about engineering ideas about acceptable accuracy. A 50% error in
half-life would be invisible seen on the tremendous range of figure
14.10. Being wrong by a factor 10, or even a factor
100, two orders of magnitude, is ho-hum on the scale that the
half-life varies. So, the potential energy 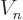 inside the nucleus
can be ballparked. The current results use the typical value of
inside the nucleus
can be ballparked. The current results use the typical value of  35
MeV given in [31, p. 252].
35
MeV given in [31, p. 252].
That leaves the value of 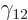 to be found from the integral
over the barrier in (14.12). Because the nuclear forces are
so short-range, they should be negligible over most of the integration
range. So it seems reasonable to simply substitute the Coulomb
potential everywhere for
to be found from the integral
over the barrier in (14.12). Because the nuclear forces are
so short-range, they should be negligible over most of the integration
range. So it seems reasonable to simply substitute the Coulomb
potential everywhere for 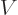 . The Coulomb potential is
inversely proportional to the radial position
. The Coulomb potential is
inversely proportional to the radial position  , and it equals
, and it equals
 at
at 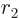 , so
, so 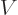 can be written as
can be written as 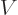

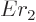

 . Substituting this in, and doing the integral by
making a change of integration variable to
. Substituting this in, and doing the integral by
making a change of integration variable to 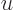 with
with 

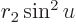 , produces
, produces
The last two terms within the square brackets are typically relatively
small compared to the first one, because 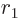 is usually fairly small
compared to
is usually fairly small
compared to 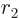 . Then
. Then 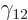 is about proportional to
is about proportional to
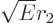 . But
. But 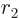 itself is inversely proportional to
itself is inversely proportional to
 , because the total energy of the alpha particle equals its
potential energy at
, because the total energy of the alpha particle equals its
potential energy at 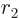 ;
;
That makes 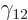 about proportional to 1
about proportional to 1
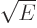 for a
given atomic number
for a
given atomic number 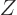 .
.
So if you plot the half-life on a logarithmic scale, and the energy
 on an reciprocal square root scale, as done in figure
14.10, they should vary linearly with each other for a
given atomic number. This does assume that the variations in number
of escape attempts are also ignored. The predicted slope of linear
variation is indicated by the
on an reciprocal square root scale, as done in figure
14.10, they should vary linearly with each other for a
given atomic number. This does assume that the variations in number
of escape attempts are also ignored. The predicted slope of linear
variation is indicated by the stems
on the cherries in
figure 14.10. Ideally, all cherries connected by
branches should fall on a single line with this slope. The figure
shows that this is quite reasonable for even-even nuclei, considering
the rough approximations made. For nuclei that are not even-even, the
deviations from the predicted slope are more significant. The next
subsection discusses the major sources of error.
Figure 14.12:
Half-life predicted by the Gamow / Gurney & Condon
theory versus the true value. Top: even-even nuclei only.
Bottom: all the nuclei except 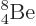 (55
as versus 67 as).
[pdf]
(55
as versus 67 as).
[pdf]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(300,21...
...,0)[b]{1Ey}}
\put(115,-9.5){\makebox(0,0)[b]{true}}
\end{picture}
\end{figure}](img3132.gif) |
The bottom line question is whether the theory, rough as it may be,
can produce meaningful values for the experimental half-lives, within
reason. Figure 14.12 shows predicted half-lives versus
the actual ones. Cherries on the black line indicate that the correct
value is predicted. It is clear that there is no real accuracy to the
predictions in any normal sense; they are easily off by several orders
of magnitude. What can you expect without an accurate model of the
nucleus itself? However, the predictions do successfully reproduce
the tremendous range of half-lives and they do not deviate from the
correct values that much compared to that tremendous range. It is
hard to imagine any other theory besides tunneling that could do the
same.
The worst performance of the theory is for the
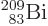 bismuth isotope indicated by the
rightmost dot in figure 14.12. Its true half-life of 19
Ey, 19 10
bismuth isotope indicated by the
rightmost dot in figure 14.12. Its true half-life of 19
Ey, 19 10 years, is grossly underestimated to be just 9 Py, 9 10
years, is grossly underestimated to be just 9 Py, 9 10 years. Then again, since the universe has only existed about 14 10
years. Then again, since the universe has only existed about 14 10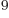 years, who is going to live long enough to complain about it?
Essentially none of the bismuth-209 that has ever been created in the
universe has decayed. It took until 2003 for physicists to observe
that bismuth-209 actually did decay; it is still listed as stable in
many references. For
years, who is going to live long enough to complain about it?
Essentially none of the bismuth-209 that has ever been created in the
universe has decayed. It took until 2003 for physicists to observe
that bismuth-209 actually did decay; it is still listed as stable in
many references. For 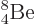 , which is not
shown in the figure, the predicted half-life is 55 as (55 10
, which is not
shown in the figure, the predicted half-life is 55 as (55 10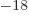 s),
versus a true value of 67 as.
s),
versus a true value of 67 as.
14.11.3 Draft: Forbidden decays
You may wonder why there is so much error in the theoretical
predictions of the half life. Or why the theory seems to work so much
better for even-even nuclei than for others. A deviation by a factor
2 000 like for bismuth-209 seems an awful lot, rough as the theory
may be.
Some of the sources of inaccuracy are self-evident from the
theoretical description as given. In particular, there is the already
mentioned effect of the value of 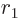 . It is certainly
possible to correct for deviations from the Coulomb potential near the
nucleus by a suitable choice of the value of
. It is certainly
possible to correct for deviations from the Coulomb potential near the
nucleus by a suitable choice of the value of 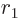 . However,
the precise value that kills off the error is unknown, and
unfortunately the results strongly depend on that value. To fix this
would require an accurate evaluation of the nuclear force potential,
and that is very difficult. Also, the potential of the electrons
would have to be included. The alpha particle does reach a distance
of the order of a tenth of a Bohr radius from the nucleus at the end
of tunneling. The Bohr radius is here taken to be based on the actual
nuclear charge, not the hydrogen one.
. However,
the precise value that kills off the error is unknown, and
unfortunately the results strongly depend on that value. To fix this
would require an accurate evaluation of the nuclear force potential,
and that is very difficult. Also, the potential of the electrons
would have to be included. The alpha particle does reach a distance
of the order of a tenth of a Bohr radius from the nucleus at the end
of tunneling. The Bohr radius is here taken to be based on the actual
nuclear charge, not the hydrogen one.
Also, the picture of a relatively compact wave packet of the alpha
particle rattling around
assumes that that the size of
that wave packet is small compared to the nucleus. That spatial
localization is associated with increased uncertainty in momentum,
which implies increased energy. And the kinetic energy of the alpha
particle is not really known anyway, without an accurate value for the
nuclear force potential.
A very major other problem is the assumption that the final alpha
particle and nucleus end up in their ground states. If either ends up
in an excited state, the energy that the alpha particle has available
for escape will be correspondingly reduced. Now the alpha particle
will most certainly come out in its ground state; it takes over 20 MeV
to excite an alpha particle. But for most nuclei, the remaining
nucleus cannot be in its ground state if the mechanism is as
described.
The main reason is angular momentum conservation. The alpha particle
has no net internal angular angular momentum. Also, it was assumed
that the alpha particle comes out radially, which means that there is
no orbital angular momentum either. So the angular momentum of the
nucleus after emission must be the same as that of the nucleus before
the emission. That is no problem for even-even nuclei, because it is
the same; even-even nuclei all have zero internal angular momentum in
their ground state. So even-even nuclei do not suffer from this
problem.
However, almost all other nuclei do. All even-odd and odd-even nuclei
and almost all odd-odd ones have nonzero angular momentum in their
ground state. Usually the initial and final nuclei have different
values. That means that alpha decay that leaves the final nucleus in
its ground state violates conservation of angular momentum. The decay
process is called “forbidden.” The final nucleus must be excited if the process is
as described. That energy subtracts from that of the alpha particle.
Therefore the alpha particle has less energy to tunnel through, and the
true half-life is much longer than computed.
Note in the bottom half of figure 14.12 how many nuclei
that are not even-even do indeed have half-lifes that are orders of
magnitude larger than predicted by theory. Consider the example of
bismuth-209, with a half-life 2 000 times longer than predicted.
Bismuth-209 has a spin, i.e. an azimuthal quantum number, of  .
However, the decay product thallium-205 has spin
.
However, the decay product thallium-205 has spin 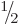 in its ground
state. If you check out the excited states of thallium-205, there is
an excited state with spin
in its ground
state. If you check out the excited states of thallium-205, there is
an excited state with spin  , but its excitation energy would
reduce the energy of the alpha particle from 3.2 MeV to 1.7 MeV,
making the tunneling process very much slower.
, but its excitation energy would
reduce the energy of the alpha particle from 3.2 MeV to 1.7 MeV,
making the tunneling process very much slower.
And there is another problem with that. The decay to the mentioned
exited state is not possible either, because it violates conservation
of parity, chapter 7.3 and 7.4. Saying
the alpha particle comes out radially,
as done above
is not really correct. The proper quantum way to say that the alpha
particle comes out with no orbital angular momentum is to say that its
wave function varies with angular location as the spherical harmonic
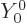 , chapter 4.2.3. In spectroscopic terms, it
, chapter 4.2.3. In spectroscopic terms, it
comes out in an s-wave.
Now the initial bismuth atom
has odd parity; its complete wave function changes sign if you
everywhere replace  by
by 
 . But the alpha particle, the
excited thallium state, and the
. But the alpha particle, the
excited thallium state, and the 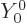 orbital motion all have even
parity; there is no change of sign. That means that the total final
parity is even too, so the final parity is not the same as the initial
parity. That violates conservation of parity so the process cannot
occur.
orbital motion all have even
parity; there is no change of sign. That means that the total final
parity is even too, so the final parity is not the same as the initial
parity. That violates conservation of parity so the process cannot
occur.
Thallium-205 does not have excited states below 3.2 MeV that have been
solidly established to have spin  and odd parity, so you may
start to wonder whether alpha decay for bismuth-209 is possible at
all. However, the alpha particle could of course come out with
orbital angular momentum. In other words it could come out with a
wave function that has an angular dependence according to
and odd parity, so you may
start to wonder whether alpha decay for bismuth-209 is possible at
all. However, the alpha particle could of course come out with
orbital angular momentum. In other words it could come out with a
wave function that has an angular dependence according to 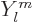 with
the azimuthal quantum number
with
the azimuthal quantum number  equal to one or more. These states
have even parity if
equal to one or more. These states
have even parity if  is even and odd parity when
is even and odd parity when  is odd.
Quantum mechanics then allows the thallium-205 excited state to have
any spin
is odd.
Quantum mechanics then allows the thallium-205 excited state to have
any spin  in the range
in the range 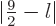
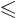

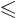
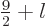 as long as
its parity is odd or even whenever
as long as
its parity is odd or even whenever  is even or odd.
is even or odd.
For example, bismuth-209 could decay to the ground state of
thallium-205 if the orbital angular momentum of the alpha particle is

 5. Or it could decay to an excited
5. Or it could decay to an excited 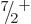 state with an
excitation energy of 0.9 MeV if
state with an
excitation energy of 0.9 MeV if 
 1. The problem is that the
kinetic energy in the angular motion subtracts from that available for
the radial motion, making the tunneling, once again, much slower. In
terms of the radial motion, the angular momentum introduces an
additional effective potential
1. The problem is that the
kinetic energy in the angular motion subtracts from that available for
the radial motion, making the tunneling, once again, much slower. In
terms of the radial motion, the angular momentum introduces an
additional effective potential 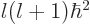

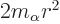 ,
compare the analysis of the hydrogen atom in chapter 4.3.2.
Note that this effect increases rapidly with
,
compare the analysis of the hydrogen atom in chapter 4.3.2.
Note that this effect increases rapidly with  . However, the
decay of bismuth-209 appears to be to the ground state anyway; the
measured energy of the alpha particle turns out to be 3.14 MeV. The
predicted half-life including the effective potential is found to be
4.6 Ey, much better than the one computed in the previous section.
. However, the
decay of bismuth-209 appears to be to the ground state anyway; the
measured energy of the alpha particle turns out to be 3.14 MeV. The
predicted half-life including the effective potential is found to be
4.6 Ey, much better than the one computed in the previous section.
One final source of error should be mentioned. Often alpha decay can
proceed in a number of ways and to different final excitation
energies. In that case, the specific decay rates must be added
together. This effect can make the true half-life shorter than the
one computed in the previous subsection. But clearly, this effect
should be minor on the scale of half-lifes of figure
14.12. Indeed, while the predicted half-lifes of many
nuclei are way below the true value in the figure, few are
significantly above it.
14.11.4 Draft: Why alpha decay?
The final question that begs an answer is why do so many nuclei so
specifically want to eject an helium-4 nucleus? Why none of the other
nuclei? Why not the less tightly bound, but lighter deuteron, or the
more tightly bound, but heavier carbon-12 nucleus? The answer is
subtle.
To understand the reason, reconsider the analysis of the previous
subsection for a more general ejected nucleus. Assume that the
ejected particle has an atomic number 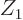 and mass
and mass 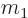 . As
mentioned, the precise number of escape attempts is not really that
important for the half life; almost all the variation in half-life is
through the quantity
. As
mentioned, the precise number of escape attempts is not really that
important for the half life; almost all the variation in half-life is
through the quantity 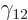 . Also, to a first
approximation the ratio of start to end of the tunneling domain,
. Also, to a first
approximation the ratio of start to end of the tunneling domain,
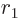

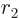 , can be ignored. Under those conditions,
, can be ignored. Under those conditions,
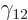 is proportional to
is proportional to
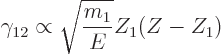
It is pretty much all in there.
As long as the ejected particle has about the usual 8 MeV binding
energy per nucleon, the square root in the expression above does not
vary that much. In such cases the energy release  is about
proportional to the amount of nucleons ejected. Table 14.3
gives some example numbers. That makes
is about
proportional to the amount of nucleons ejected. Table 14.3
gives some example numbers. That makes 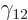 about
proportional to
about
proportional to 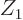 , and the greatest chance of tunneling out
then occurs by far for the lightest nuclei. It explains why the alpha
particle tunnels out instead of heavier nuclei. It is not that a
heavier nucleus like carbon-14 cannot be emitted, it is just
that an alpha particle has already done so long before carbon-14 gets
the chance. In fact, for radium-223 it has been found that one
carbon-14 nucleus is ejected for every billion alpha particles. That
is about consistent with the computed half-lifes of the events as
shown in table 14.3.
, and the greatest chance of tunneling out
then occurs by far for the lightest nuclei. It explains why the alpha
particle tunnels out instead of heavier nuclei. It is not that a
heavier nucleus like carbon-14 cannot be emitted, it is just
that an alpha particle has already done so long before carbon-14 gets
the chance. In fact, for radium-223 it has been found that one
carbon-14 nucleus is ejected for every billion alpha particles. That
is about consistent with the computed half-lifes of the events as
shown in table 14.3.
Table 14.3:
Candidates for nuclei ejected by uranium-238, radium-223, and
fermium-256.
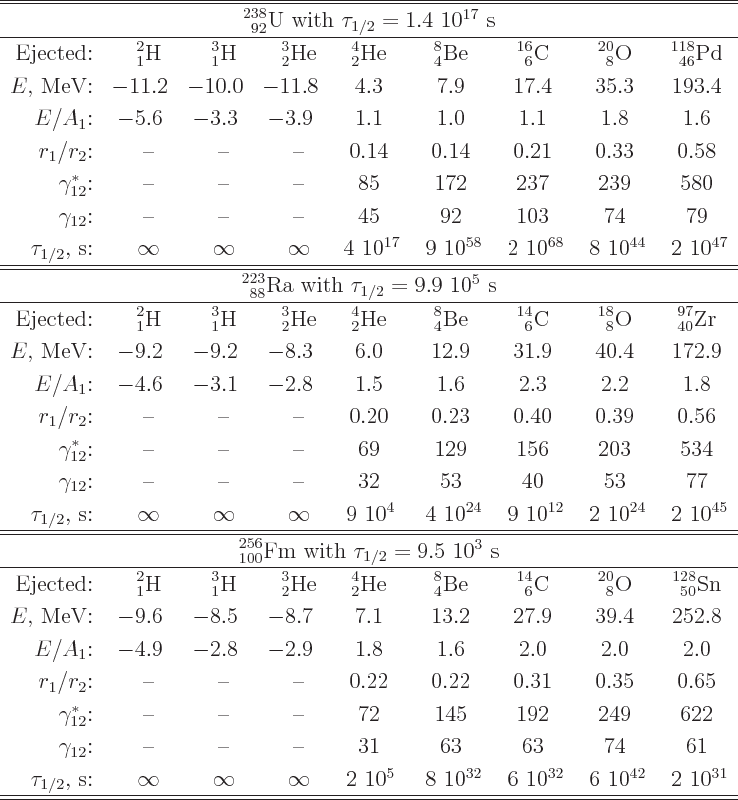 |
But the argument that 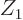 should be as small as possible should make
protons or neutrons, not the alpha particle, the ones that can escape
most easily. However, these do not have any binding energy. While
protons or neutrons are indeed ejected from nuclei that have a very
large proton, respectively neutron excess, normally the energy release
for such emissions is negative. Therefore the emission cannot occur.
Beta decay occurs instead to adjust the ratio between protons and
neutrons to the optimum value. Near the optimum value, you would
still think it might be better to eject a deuteron than an alpha.
However, because the binding energy of the deuteron is only a single
MeV per nucleon, the energy release is again negative. Among the
light nuclei, the alpha is unique in having almost the full 8 MeV of
binding energy per nucleon. It is therefore the only one that produces
a positive energy release.
should be as small as possible should make
protons or neutrons, not the alpha particle, the ones that can escape
most easily. However, these do not have any binding energy. While
protons or neutrons are indeed ejected from nuclei that have a very
large proton, respectively neutron excess, normally the energy release
for such emissions is negative. Therefore the emission cannot occur.
Beta decay occurs instead to adjust the ratio between protons and
neutrons to the optimum value. Near the optimum value, you would
still think it might be better to eject a deuteron than an alpha.
However, because the binding energy of the deuteron is only a single
MeV per nucleon, the energy release is again negative. Among the
light nuclei, the alpha is unique in having almost the full 8 MeV of
binding energy per nucleon. It is therefore the only one that produces
a positive energy release.
The final problem is that the arguments above seem to show that
spontaneous fission cannot occur. For, is the fission of say
fermium-256 into two tin-128 nuclei not just ejection of a tin-128
nucleus, leaving a tin-128 nucleus? The arguments above say that
alpha decay should occur much before this can happen.
The problem is that the analysis of alpha decay is inapplicable to
fission. The numbers for fission-scale half-lifes in table
14.3 are all wrong. Fission is indeed a tunneling event.
However, it is one in which the energy barrier is disintegrating due
to a global instability of the nuclear shape. That instability
mechanism strongly favors large scale division over short scale ones.
The only hint of this in table 14.3 are the large values of
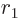

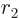 for fission-scale events. When
for fission-scale events. When 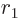

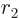 becomes one, the
tunneling region is gone. But long before that happens, the region is
so small compared to the size of the ejected nucleus that the basic
ideas underlying the analysis have become meaningless. Even ignoring
the fact that the nuclear shapes have been assumed spherical and they
are not in fission.
becomes one, the
tunneling region is gone. But long before that happens, the region is
so small compared to the size of the ejected nucleus that the basic
ideas underlying the analysis have become meaningless. Even ignoring
the fact that the nuclear shapes have been assumed spherical and they
are not in fission.
Thus, unlike table 14.3 suggests, fermium-256 does fission.
The two fragments are usually of different size, but not vastly so.
About 92% of fermium-256 nuclei spontaneously fission, while the
other 8% experience alpha decay. Uranium-238 decays for
99.999 95% through 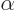 decay, and for only 0.000 05%
through spontaneous fission. Although the amount of fission is very
small, it is not by far as small as the numbers in table
14.3 imply. Fission is not known to occur for radium-223;
this nucleus does indeed show pure alpha decay except for the
mentioned rare carbon-14 emission.
decay, and for only 0.000 05%
through spontaneous fission. Although the amount of fission is very
small, it is not by far as small as the numbers in table
14.3 imply. Fission is not known to occur for radium-223;
this nucleus does indeed show pure alpha decay except for the
mentioned rare carbon-14 emission.
![]()
![]()
![]() ,
,![]()
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,37...
...ebox(0,0)[b]{5}}
\put(-66,210){\makebox(0,0)[b]{6}}
\end{picture}
\end{figure}](img3114.gif)
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() -
-![]() .
.![]() ,
,![]() .
.![]() ,
,![]()
![]()
![]() ;
;![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;![]()
![]()
![]() .
.![]()
![]()
![]() 3
3![]()
![]() .
.![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![\begin{displaymath}
\gamma_{12} = \frac{\sqrt{2m_\alpha E}}{\hbar} r_2
\left[
...
...rac{r_1}{r_2}\right)}
-\arcsin\sqrt{\frac{r_1}{r_2}}
\right]
\end{displaymath}](img3128.gif)
![]()
![]() .
.![]()
![]() .
.![]()
![]() ,
,![]() ;
;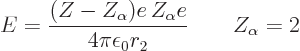
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(300,21...
...,0)[b]{1Ey}}
\put(115,-9.5){\makebox(0,0)[b]{true}}
\end{picture}
\end{figure}](img3132.gif)
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() .
.![]() .
.![]() .
.![]()
![]() ,
,![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]() .
.![]() .
.![]()
![]()
![]() ,
,![]()
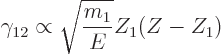
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()