| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
14.10 Draft: Liquid drop model
Nucleons attract each other with nuclear forces that are not
completely understood, but that are known to be short range. That is
much like molecules in a classical liquid drop attract each other with
short-range Van der Waals forces. Indeed, it turns out that a liquid
drop model can explain many properties of nuclei surprisingly well.
This section gives an introduction.
14.10.1 Draft: Nuclear radius
The volume of a liquid drop, hence its number of molecules, is
proportional to the cube of its radius 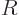 . Conversely, the
radius is proportional to the cube root of the number of molecules.
Similarly, the radius of a nucleus is approximately equal to the cube
root of the number of nucleons:
. Conversely, the
radius is proportional to the cube root of the number of molecules.
Similarly, the radius of a nucleus is approximately equal to the cube
root of the number of nucleons:
![\begin{displaymath}
R \approx R_A \sqrt[3]{A} \qquad R_A = 1.23 \mbox{ fm} %
\end{displaymath}](img3094.gif) |
(14.9) |
Here  is the mass number, equal to the number of protons
is the mass number, equal to the number of protons 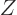 plus
the number of neutrons
plus
the number of neutrons 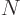 . Also fm stands for
. Also fm stands for
femtometer,
equal to 10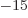 meter; it may be
referred to as a “fermi” in some older references. Enrico Fermi was a great
curse for early nuclear physicists, quickly doing all sorts of things
before they could.
meter; it may be
referred to as a “fermi” in some older references. Enrico Fermi was a great
curse for early nuclear physicists, quickly doing all sorts of things
before they could.
It should be noted that the above nuclear radius is an average one. A
nucleus does not stop at a very sharply defined radius. (And neither
would a liquid drop if it only contained 100 molecules or so.) Also,
the constant 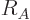 varies a bit with the nucleus and with the method
used to estimate the radius. Values from 1.2 to 1.25 are typical.
This book will use the value 1.23 stated above.
varies a bit with the nucleus and with the method
used to estimate the radius. Values from 1.2 to 1.25 are typical.
This book will use the value 1.23 stated above.
It may be noted that these results for the nuclear radii are quite
solidly established experimentally. Physicists have used a wide
variety of ingenious methods to verify them. For example, they have
bounced electrons at various energy levels off nuclei to probe their
Coulomb fields, and alpha particles to also probe the nuclear forces.
They have examined the effect of the nuclear size on the electron
spectra of the atoms; these effects are very small, but if you
substitute a muon for an electron, the effect becomes much larger
since the muon is much heavier. They have dropped pi mesons on nuclei
and watched their decay. They have also compared the energies of
nuclei with 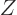 protons and
protons and 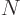 neutrons against the corresponding
neutrons against the corresponding
mirror nuclei
that have with 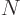 protons and
protons and 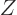 neutrons. There is good evidence that the nuclear force is the same
when you swap neutrons with protons and vice versa, so comparing such
nuclei shows up the Coulomb energy, which depends on how tightly the
protons are packed together. All these different methods give
essentially the same results for the nuclear radii. They also
indicate that the neutrons and protons are well-mixed throughout the
nucleus, [31, pp. 44-59]
neutrons. There is good evidence that the nuclear force is the same
when you swap neutrons with protons and vice versa, so comparing such
nuclei shows up the Coulomb energy, which depends on how tightly the
protons are packed together. All these different methods give
essentially the same results for the nuclear radii. They also
indicate that the neutrons and protons are well-mixed throughout the
nucleus, [31, pp. 44-59]
14.10.2 Draft: von Weizsäcker formula
The binding energy of nuclei can be approximated by the “von Weizsäcker formula,“ or “Bethe-von Weizsäcker formula:”
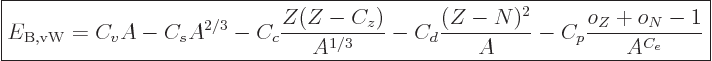 |
(14.10) |
where the 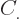 are constants, while
are constants, while 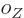 is 1 if the number of
protons is odd and zero if it is even, and similar for
is 1 if the number of
protons is odd and zero if it is even, and similar for 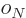 for
neutrons. This book uses values given by [37]
for the constants:
for
neutrons. This book uses values given by [37]
for the constants:
where a MeV (mega electron volt) is 1.602 18 10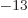 J, equal to the
energy that an electron picks up in a one million volt electric field.
J, equal to the
energy that an electron picks up in a one million volt electric field.
Plugged into the mass-energy relation, the von Weizsäcker formula
produces the so-called “semi-empirical mass formula:”
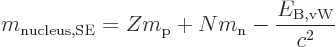 |
(14.11) |
14.10.3 Draft: Explanation of the formula
The various terms in the von Weizsäcker formula of the previous
subsection have quite straightforward explanations. The 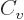 term is
typical for short-range attractive forces; it expresses that the
energy of every nucleon is lowered the same amount by the presence of
the attracting nucleons in its immediate vicinity. The classical
analogue is that the energy needed to boil away a drop of liquid is
proportional to its mass, hence to its number of molecules.
term is
typical for short-range attractive forces; it expresses that the
energy of every nucleon is lowered the same amount by the presence of
the attracting nucleons in its immediate vicinity. The classical
analogue is that the energy needed to boil away a drop of liquid is
proportional to its mass, hence to its number of molecules.
The 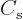 term expresses that nucleons near the surface are not
surrounded by a complete set of attracting nucleons. It raises their
energy. This affects only a number of nucleons proportional to the
surface area, hence proportional to
term expresses that nucleons near the surface are not
surrounded by a complete set of attracting nucleons. It raises their
energy. This affects only a number of nucleons proportional to the
surface area, hence proportional to 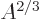 . The effect is
negligible for a classical drop of liquid, which may have a million
molecules along a diameter, but not for a nucleus with maybe ten
nucleons along it. (Actually, the effect is important for a classical
drop too, even if it does not affect its overall energy, as it gives
rise to surface tension.)
. The effect is
negligible for a classical drop of liquid, which may have a million
molecules along a diameter, but not for a nucleus with maybe ten
nucleons along it. (Actually, the effect is important for a classical
drop too, even if it does not affect its overall energy, as it gives
rise to surface tension.)
The 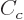 term expresses the Coulomb repulsion between protons. Like
the Coulomb energy of a sphere with constant charge density, it is
proportional to the square net charge, so to
term expresses the Coulomb repulsion between protons. Like
the Coulomb energy of a sphere with constant charge density, it is
proportional to the square net charge, so to 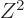 and inversely
proportional to the radius, so to
and inversely
proportional to the radius, so to 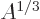 . However, the
empirical constant
. However, the
empirical constant 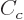 is somewhat different from that of a constant
charge density. Also, a correction
is somewhat different from that of a constant
charge density. Also, a correction 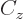
 1 has been thrown in
to ensure that there is no Coulomb repulsion if there is just one
proton.
1 has been thrown in
to ensure that there is no Coulomb repulsion if there is just one
proton.
The last two terms cheat; they try to deviously include quantum
effects in a supposedly classical model. In particular, the 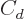 term adds an energy increasing with the square of the difference in
number of protons and neutrons. It simulates the effect of the Pauli
exclusion principle. Assume first that the number of protons and
neutrons is equal, each
term adds an energy increasing with the square of the difference in
number of protons and neutrons. It simulates the effect of the Pauli
exclusion principle. Assume first that the number of protons and
neutrons is equal, each 
 2. In that case the protons will be able
to occupy the lowest
2. In that case the protons will be able
to occupy the lowest 
 2 proton energy levels, and the neutrons the
lowest
2 proton energy levels, and the neutrons the
lowest 
 2 neutron levels. However, if then, say, some of the
protons are turned into neutrons, they will have to move to energy
levels above
2 neutron levels. However, if then, say, some of the
protons are turned into neutrons, they will have to move to energy
levels above 
 2, because the lowest
2, because the lowest 
 2 neutron levels are
already filled with neutrons. Therefore the energy goes up if the
number of protons and neutrons becomes unequal.
2 neutron levels are
already filled with neutrons. Therefore the energy goes up if the
number of protons and neutrons becomes unequal.
The last 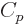 term expresses that nucleons of the same type like to
pair up. When both the number of protons and the number of neutrons
is even, all protons can pair up, and all neutrons can, and the energy
is lower than average. When both the number of protons is odd and the
number of neutrons is odd, there will be an unpaired proton as well as
an unpaired neutron, and the energy is higher than average.
term expresses that nucleons of the same type like to
pair up. When both the number of protons and the number of neutrons
is even, all protons can pair up, and all neutrons can, and the energy
is lower than average. When both the number of protons is odd and the
number of neutrons is odd, there will be an unpaired proton as well as
an unpaired neutron, and the energy is higher than average.
14.10.4 Draft: Accuracy of the formula
Figure 14.9 shows the error in the von Weizsäcker
formula as colors. Blue means that the actual binding energy is
higher than predicted, red that it is less than predicted. For very
light nuclei, the formula is obviously useless, but for the remaining
nuclei it is quite good. Note that the error is in the order of MeV,
to be compared to a total binding energy of about 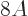 MeV. So for
heavy nuclei the relative error is small.
MeV. So for
heavy nuclei the relative error is small.
Figure 14.9:
Error in the von
Weizsäcker formula.
[pdf][con]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,56...
...]{$>$14 MeV more than estimated}}
}
\end{picture}}
\end{picture}
\end{figure}](img3112.gif) |
Near the magic numbers the binding energy tends to be greater than the
predicted values. This can be qualitatively understood from the
quantum energy levels that the nucleons occupy. When nucleons are
successively added to a nucleus, those that go into energy levels just
below the magic numbers have unusually large binding energy, and the
total nuclear binding energy increases above that predicted by the von
Weizsäcker formula. The deviation from the formula therefore tends
to reach a maximum at the magic number. Just above the magic number,
further nucleons have a much lower energy level, and the deviation
from the von Weizsäcker value decreases again.
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()