|
|
|
|
|
Next: 14.10 Draft: Liquid drop model |
|
This book largely limits itself to relatively simple, but effective, models for nuclei. However, the deuteron, the deuterium nucleus, is the most simple nontrivial nucleus, as it consists of only a single proton. So, to give a rough idea of what sort of more advanced nuclear theories there are out there, this one section will look at the deuteron in some more detail.
Addendum {A.41} explores some of the nuclear potentials that you can write down to model the deuteron. Simple potentials such as those described there give a lot of insight in the deuteron. They give ballpark values for the potential and kinetic energies. They also give an explanation for the observations that the deuteron is only weakly bound and that there is no second bound state. They show the relatively large size of the deuteron: there is a good chance that the proton and neutron can be found way apart. Simple additions to the potential can describe the spin dependence and the violation of orbital angular momentum conservation.
However, there is a problem. These potentials describe a deuteron consisting of a proton and a neutron. But the proton and neutron are not elementary particles: each consists of three quarks.
This internal structure should not be a much of a concern when the proton and neutron are relatively far apart. But if the two get really close? Surely in that case the physics should be described in terms of six quarks that interact through gluons and the Pauli exclusion principle, [5, p. 95]? Eventually the proton and neutron must lose their identity. Then there is no longer any reasonable justification for a picture of a free-space proton interacting with a free-space neutron.
A rough idea of the scales involved may be obtained by looking at charge radii. The charge radius of a particle is a measure of the size of its charge distribution. Now the proton has a charge radius of about 0.88 fm. The deuteron has a charge radius of 2.14 fm. So at least the charge radius of a proton is not that much smaller than the size of the deuteron. And a quantum description of the deuteron needs to consider all possible nucleon spacings. Clearly for the smallest nucleon spacings, the two must intrude nontrivially into each other’s space.
Consider another example of compound structures, noble gas atoms. When such atoms are relatively far apart, they can be modeled well as point particles forming an ideal gas. You might add some simple Van der Waals forces to that picture. However, when the atoms get pushed close together, the electromagnetic interactions between them become much more complex. And if you try to push the atoms even closer together, they resist that very strongly. The reason is the Pauli exclusion principle, chapter 5.10. More than two electrons cannot be pushed in the same spatial state.
The big difference is of course that the electromagnetic interactions of the electrons and nuclei that make up atoms are well understood. There is as yet no good way to describe the color force interactions between the quarks that make up nucleons. (Certainly not at the relatively low energies of importance for nuclear structure.)
Physicists have developed a model that is somewhere intermediate between
that of interacting free-space nucleons and interacting quarks. In the
model, the forces between nucleons are produced by the exchange of
particles called “pions.” That is much like how in relativistic quantum mechanics,
electromagnetic forces are produced by the exchange of photons. Or how
the forces between quarks are believed to be produced by the exchange of
gluons. These exchanged particles are virtual
ones.
Roughly speaking, relativistic mass-energy equivalence combined with quantum uncertainty in energy allows some possibility for these particles to be found near the real particles. (See addendum {A.42} for a more quantitative description of these ideas.)
The picture is now that the proton and neutron are elementary
particles but dressed
in a coat of virtual pions.
Pions consist of two quarks. More precisely, they consist of a quark
and an antiquark. There are three pions; the positively charged
![]() ,
,![]() ,
,![]() .
.
When the neutron and proton exchange a pion, they also exchange its momentum. That produces a force between them.
There are a number of redeeming features to this model:
However, the same result is often derived much quicker and easier in
literature. That derivation does not require any Hamiltonians to be
written down, or even any mathematics above the elementary school
level. It uses the popular so-called “energy-time
uncertainty equality,” chapter 7.2.2,
(OK, someone might object the pions do most decidedly not pop up and disappear again. The ground state of a nucleus is an energy eigenstate and those are stationary, chapter 7.1.4. But why worry about such minor details?)

The magnetic moment of the neutron can similarly be written
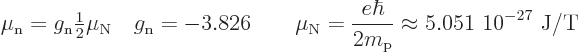
Suppose however that the neutron occasionally briefly flips out a
negatively charged virtual ![]() .
.
Similar ideas apply for the proton. The proton may temporarily flip
out a positively charged ![]() ,
,
Apparently then, the virtual ![]()
![]() -
-![]()
![]() -
-![]() 3
3![]() -
-![]() 3
3
The slightly larger value seems logical enough too. The fact that
the proton turns occasionally into a neutron should decrease its
total magnetic moment. Conversely, the neutron occasionally turns
into a proton. Assume that the neutron has half a unit of spin in
the positive chosen ![]() -
-![]()
![]()
![]() -
-
The more reasonable explanation is that the proton catches a virtual
![]()
![]()
OPEP,for One Pion Exchange Potential, {A.42}.
There are also drawbacks to the pion exchange approach.
For one, the magnetic moments of the neutron and proton can be reasonably explained by simply adding those of the constituent quarks, [31, pp. 74, 745]. To be sure, that does not directly affect the question whether the pion exchange model is useful. But it does make the dressed nucleon picture look quite contrived.
A bigger problem is nucleon spacings that are not so large. One-pion exchange is generally believed to be dominant for nucleon spacings above 3 fm, and reasonable for spacings above 2 fm, [36, p. 135, 159], [5, p. 86, 91]. However, things get much more messy for spacings shorter than that. That includes the vital range of spacings of the primary nucleon attractions and repulsions. For these, two-pion exchange must be considered. In addition, excited pion states and an excited nucleon state need to be included. That is much more complicated. See addendum {A.42} for a brief intro to some of the issues involved.
And for still shorter nucleon spacings, things get very messy indeed, including multi-pion exchanges and a zoo of other particles. Eventually the question must be at what spacing nucleons lose their distinctive character and a model of quarks exchanging gluons becomes unavoidable. Fortunately, very close spacings correspond to very high energies since the nucleons strongly repel each other at close range. So very close spacings may not be that important for most nuclear physics.
Because of the above and other issues, many physicists use a less theoretical approach. The OPEP is still used at large nucleon spacings. But at shorter spacings, relatively simple chosen potentials are used. The parameters of those “phenomenological” potentials are adjusted to match the experimental data.
It makes things a lot simpler. And it is not clear whether the theoretical models used at smaller nucleon spacings are really that much more justified. However, phenomenological potentials do require that large numbers of parameters are fit to experimental data. And they have a nasty habit of not working that well for experimental data different from that used to define their parameters, [32].
Regardless of potential used, it is difficult to come up with an
unambiguous probability for the ![]()
![]()
Then there is the very big problem of generalizing all this to systems of three or more nucleons. One current hope is that closer examination of the underlying quark model may produce a more theoretically justified model in terms of nucleons and mesons, [32].