| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
14.13 Draft: Collective Structure
Some nuclear properties are difficult to explain using the shell model
approach as covered here. Therefore physicists have developed
different models.
For example, nuclei may have excited states with unexpectedly low
energy. One example is ruthenium-104 in figure 14.20,
and many other even-even nuclei with such energies may be found in
figure 14.19. If you try to explain the excitation energy
within a shell model context, you are led to the idea that many shell
model excitations combine forces, as in section 14.12.5.
Then there are nuclei for which the normal shell model does not work
at all. They are called the nonspherical or deformed nuclei. Among
the line of most stable nuclei, they are roughly the “rare
earth” lanthanides and the extremely heavy actinides that are
deformed. In terms of the mass number, the ranges are about 150 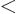

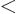 190 and 220
190 and 220 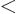
 . (However, various very
unstable lighter nuclei are quite nonspherical too. None of this is
written in stone.) In terms of figure 14.19, they are the
very small squares. Examples are hafnium-176 in figure
14.20 and tantalum-181 in figure
14.21.
. (However, various very
unstable lighter nuclei are quite nonspherical too. None of this is
written in stone.) In terms of figure 14.19, they are the
very small squares. Examples are hafnium-176 in figure
14.20 and tantalum-181 in figure
14.21.
It seems clear that many or all nuclei participate in these effects.
Trying to explain such organized massive nucleon participation based
on a perturbed basic shell model alone would be very difficult, and
mathematically unsound in the case of deformed nuclei. A completely
different approach is desirable.
Nuclei with many nucleons and densely spaced energy levels bear some
similarity to macroscopic systems. Based on that idea, physicists had
another look at the classical liquid drop model for nuclei. That
model was quite successful in explaining the size and ground state
energy levels of nuclei in section 14.10.
But liquid drops are not necessarily static; they can vibrate.
Vibrating states provide a model for low-energy excited states in
which the nucleons as a group participate nontrivially. Furthermore,
the vibrations can become unstable, providing a model for permanent
nuclear deformation or nuclear fission. Deformed nuclei can display
effects of rotation of the nuclei. This section will give a basic
description of these effects.
14.13.1 Draft: Classical liquid drop
This section reviews the mechanics of a classical liquid drop, like
say a droplet of water. However, there will be one additional effect
included that you would be unlikely to see in a drop of water: it will
be assumed that the liquid contains distributed positively charged
ions. This is needed to allow for the very important destabilizing
effect of the Coulomb forces in a nucleus.
It will be assumed that the nuclear liquid
is
homogeneous throughout. That is a somewhat doubtful assumption for a
model of a nucleus; there is no a priori reason to assume that the
proton and neutron motions are the same. But a two-liquid model, such
as found in [40, p. 183ff], is beyond the
current coverage.
It will further be assumed that the nuclear liquid preserves its
volume. This assumption is consistent with the formula
(14.9) for the nuclear radius, and it greatly simplifies
the classical analysis.
The von Weizsäcker formula showed that the nuclear potential energy
increases with the surface area. The reason is that nucleons near the
surface of the nucleus are not surrounded by a full set of attracting
neighboring nucleons. Macroscopically, this effect is explained as
“surface tension.” Surface tension is defined as increased
potential energy per unit surface area. (The work in expanding the
length of a rectangular surface area must equal the increased
potential energy of the surface molecules. From that it is seen that
the surface tension is also the tension force at the perimeter of the
surface per unit length.)
Using the surface term in the von Weizsäcker formula
(14.10) and (14.9), the nuclear equivalent of the
surface tension is
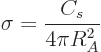 |
(14.17) |
The 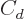 term in the von Weizsäcker formula might also be affected
by the nuclear surface area because of its unavoidable effect on the
nuclear shape, but to simplify things this will be ignored.
term in the von Weizsäcker formula might also be affected
by the nuclear surface area because of its unavoidable effect on the
nuclear shape, but to simplify things this will be ignored.
The surface tension wants to make the surface of the drop as small as
possible. It can do so by making the drop spherical. However, this
also crowds the protons together the closest, and the Coulomb
repulsions resist that. So the Coulomb term fights the trend towards
a spherical shape. This can cause heavy nuclei, for which the Coulomb
term is big, to fission into pieces. It also makes lighter nuclei
less resistant to deformation, promoting nuclear vibrations or even
permanent deformations. To include the Coulomb term in the analysis
of a classical drop of liquid, it can be assumed that the liquid is
charged, with total charge 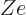 .
.
Infinitesimal vibrations of such a liquid drop can be analyzed,
{A.43}. It is then seen that the drop can vibrate
around the spherical shape with different natural frequencies. For a
single mode of vibration, the radial displacement of the surface of
the drop away from the spherical value takes the form
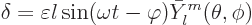 |
(14.18) |
Here 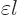 is the infinitesimal amplitude of vibration,
is the infinitesimal amplitude of vibration,
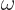 the frequency, and
the frequency, and 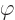 a phase angle. Also
a phase angle. Also 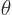 and
and 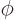 are the coordinate angles of a spherical coordinate system
with its origin at the center of the drop, N.3. The
are the coordinate angles of a spherical coordinate system
with its origin at the center of the drop, N.3. The
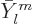 are essentially the spherical harmonics of orbital
angular momentum fame, chapter 4.2.3. However, in the
classical analysis it is more convenient to use the real version of
the
are essentially the spherical harmonics of orbital
angular momentum fame, chapter 4.2.3. However, in the
classical analysis it is more convenient to use the real version of
the 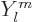 . For
. For 
 0, there is no change, and for
0, there is no change, and for 
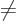 0 they can be obtained from the complex version by taking
0 they can be obtained from the complex version by taking
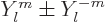 and dividing by
and dividing by 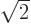 or
or 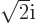 as
appropriate.
as
appropriate.
Vibration with 
 0 is not possible, because it would mean that the
radius increased or decreased everywhere, (
0 is not possible, because it would mean that the
radius increased or decreased everywhere, (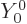 is a constant),
which would change the volume of the liquid. Motion with
is a constant),
which would change the volume of the liquid. Motion with 
 1 is
possible, but it can be seen from the spherical harmonics that this
corresponds to translation of the drop at constant velocity, not to
vibration.
1 is
possible, but it can be seen from the spherical harmonics that this
corresponds to translation of the drop at constant velocity, not to
vibration.
Vibration occurs only for 
 2, and the frequency of vibration
is then, {A.43}:
2, and the frequency of vibration
is then, {A.43}:
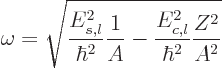 |
(14.19) |
The constants 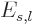 and
and  express the relative strengths
of the surface tension and Coulomb repulsions, respectively. The
values of these constants are, expressed in energy units,
express the relative strengths
of the surface tension and Coulomb repulsions, respectively. The
values of these constants are, expressed in energy units,
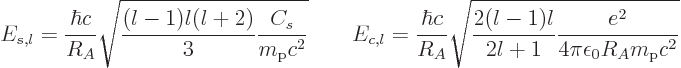 |
(14.20) |
The most important mode of vibration is the one at the lowest
frequency, which means 
 2. In that case the numerical values
of the constants are
2. In that case the numerical values
of the constants are
 |
(14.21) |
Of course a nucleus with a limited number of nucleons and energy
levels is not a classical system with countless molecules and energy
levels. The best you may hope for that there will be some reasonable
qualitative agreement between the two.
It turns out that the liquid drop model significantly overestimates
the stability of nuclei with respect to relatively small deviations
from spherical. However, it does much a better job of estimating the
stability against the large scale deformations associated with nuclear
fission.
Also, the inertia of a nucleus can be quite different from that of a
liquid drop, [36, p. 345, 576]. This however
affects 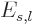 and
and  equally, and so it does not
fundamentally change the balance between surface tension and Coulomb
repulsions.
equally, and so it does not
fundamentally change the balance between surface tension and Coulomb
repulsions.
14.13.2 Draft: Nuclear vibrations
In the previous subsection, the vibrational frequencies of nuclei were
derived using a classical liquid drop model. They apply to vibrations
of infinitely small amplitude, hence infinitesimal energy.
However, for a quantum system like a nucleus, energy should be
quantized. In particular, just like the vibrations of the
electromagnetic field come in photons of energy 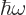 ,
you expect vibrations of matter to come in “phonons” of energy
,
you expect vibrations of matter to come in “phonons” of energy 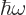 . Plugging in the
classical expression for the lowest frequency gives
. Plugging in the
classical expression for the lowest frequency gives
 |
(14.22) |
That is in the ballpark of excitation energies for nuclei, suggesting
that collective motion of the nucleons is something that must be
considered.
In particular, for light nuclei, the predicted energy is about
35
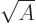 MeV, comparable to the von Weizsäcker approximation
for the pairing energy, 22
MeV, comparable to the von Weizsäcker approximation
for the pairing energy, 22
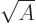 MeV. Therefore, it is in the
ballpark to explain the energy of the 2
MeV. Therefore, it is in the
ballpark to explain the energy of the 2 excitation of light
even-even nuclei in figure 14.19. The predicted energies are
however definitely too high. That reflects the fact mentioned in the
previous subsection that the classical liquid drop overestimates the
stability of nuclei with respect to small deformations. Note also the
big discrete effects of the magic numbers in the figure. Such quantum
effects are completely missed in the classical liquid drop model.
excitation of light
even-even nuclei in figure 14.19. The predicted energies are
however definitely too high. That reflects the fact mentioned in the
previous subsection that the classical liquid drop overestimates the
stability of nuclei with respect to small deformations. Note also the
big discrete effects of the magic numbers in the figure. Such quantum
effects are completely missed in the classical liquid drop model.
It should also be pointed out that now that the energy is quantized,
the basic assumption that the amplitude of the vibrations is
infinitesimal is violated. A quick ballpark shows the peak quantized
surface deflections to be in the fm range, which is not really small
compared to the nuclear radius. If the amplitude was indeed
infinitesimal, the nucleus would electrically appear as a spherically
symmetric charge distribution. Whether you want to call the
deviations from that prediction appreciable,
[36, p. 342, 354] or small,
[31, p. 152], nonzero values should certainly be expected.
As far as the spin is concerned, the classical perturbation of the
surface of the drop is given in terms of the spherical harmonics
 . The overall mass distribution has the same dependence
on angular position. In quantum terms you would associate such an
angular dependence with an azimuthal quantum number 2 and even parity,
hence with a 2
. The overall mass distribution has the same dependence
on angular position. In quantum terms you would associate such an
angular dependence with an azimuthal quantum number 2 and even parity,
hence with a 2 state. It all seems to fit together rather nicely.
state. It all seems to fit together rather nicely.
There is more. You would expect the possibility of a two-phonon
excitation at twice the energy. Phonons, like photons, are bosons; if
you combine two of them in a set of single-particle states of square
angular momentum 
 2, then the net square angular momentum can be
either 0, 2, or 4, table 12.2. So you would expect a
triplet of excited 0
2, then the net square angular momentum can be
either 0, 2, or 4, table 12.2. So you would expect a
triplet of excited 0 , 2
, 2 , and 4
, and 4 states at roughly twice the
energy of the lowest 2
states at roughly twice the
energy of the lowest 2 excited state.
excited state.
And indeed, oxygen-18 in figure 14.17 shows a nicely
compact triplet of this kind at about twice the energy of the lowest
2 state. Earlier, these states were seemingly satisfactorily
explained using single-nucleon excitations, or combinations of a few
of them. Now however, the liquid drop theory explains them, also
seemingly satisfactory, as motion of the entire nucleus!
state. Earlier, these states were seemingly satisfactorily
explained using single-nucleon excitations, or combinations of a few
of them. Now however, the liquid drop theory explains them, also
seemingly satisfactory, as motion of the entire nucleus!
That does not necessarily mean that one theory must be wrong and one
right. There is no doubt that neither theory has any real accuracy
for this nucleus. The complex actual dynamics is quite likely to
include nontrivial aspects of each theory. The question is whether
the theories can reasonably predict correct properties of the nucleus,
regardless of the approximate way that they arrive at those
predictions. Moreover, a nuclear physicist would always want to look
at the decay of the excited states, as well as their electromagnetic
properties where available, before classifying their nature. That
however is beyond the scope of this book.
Figure 14.22:
An
excitation energy ratio for even-even nuclei.
[pdf][con]
 |
Many, but by no means all, even-even nuclei show similar vibrational
characteristics. That is illustrated in figure 14.22. This
figure shows the ratio of the second excited energy level 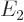 ,
regardless of spin, divided by the energy
,
regardless of spin, divided by the energy 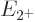 of the lowest
2
of the lowest
2 excited state. Normally
excited state. Normally 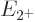 is the lowest excited state
of all, so
is the lowest excited state
of all, so 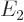 will be larger, making the ratio greater than one.
That are the nuclei we are interested in here. Helium 4, the little
black square at the
will be larger, making the ratio greater than one.
That are the nuclei we are interested in here. Helium 4, the little
black square at the 

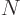
 2 intersection, is of
no interest.
2 intersection, is of
no interest.
Now the theoretically-ideal vibrating nucleus would have a 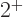 lowest excited state, corresponding to a single phonon of vibration.
It would also have a triplet of states with two phonons, where ideally
speaking all three of these states should each have an energy
lowest excited state, corresponding to a single phonon of vibration.
It would also have a triplet of states with two phonons, where ideally
speaking all three of these states should each have an energy 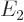 that is exactly twice the energy
that is exactly twice the energy 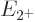 of the state with one
phonon. That makes the ideal energy ratio
of the state with one
phonon. That makes the ideal energy ratio 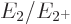 equal to 2.
The nuclei that do have that energy ratio are shown as bright green
squares in figure 14.22. These bright green squares are
likely candidates for nuclei with vibrating excited states of low
energy. But in addition, for the ideal vibrating nucleus, the triplet
of exited two-phonon states must consist of exactly one
equal to 2.
The nuclei that do have that energy ratio are shown as bright green
squares in figure 14.22. These bright green squares are
likely candidates for nuclei with vibrating excited states of low
energy. But in addition, for the ideal vibrating nucleus, the triplet
of exited two-phonon states must consist of exactly one 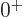 state,
exactly one
state,
exactly one 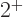 state, and exactly one
state, and exactly one 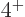 state, because that are
the only three states that the two phonons can produce. The nuclei
four which the lowest excited state is
state, because that are
the only three states that the two phonons can produce. The nuclei
four which the lowest excited state is 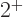 one, and the next three
states consist of one
one, and the next three
states consist of one 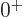 state, one
state, one 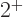 state, and one
state, and one 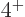 state, are marked with an
state, are marked with an V
in figure 14.22.
So bright green squares in figure 14.22 with an
V
in them are surely nuclei willing to vibrate.
Anything else would be too much of a coincidence to believe. You can
see that nuclei with vibrating excited states are quite common below
 82 neutrons, or near magic numbers.
82 neutrons, or near magic numbers.
Still, many even-even nuclei do not seem to have vibrational excited
states. But many of those who do not still have that unexpected
lowest exited state that has spin 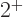 and very little
energy. Obviously, then, liquid-drop vibrations must be only a part of
the story.
and very little
energy. Obviously, then, liquid-drop vibrations must be only a part of
the story.
Figure 14.23:
Textbook
vibrating nucleus tellurium-120.
[pdf]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
% vertical spacing 137...
...\frac{29}{2}}$}}
\put(400,4){\makebox(0,0)[bl]{?}}
\end{picture}
\end{figure}](img3243.gif) |
Much heavier vibrating nuclei than oxygen-18 are tellurium-120 in
figure 14.23 as well as the earlier example of
ruthenium-104 in figure 14.20. Both nuclei have again
a fairly compact 0 , 2
, 2 , 4
, 4 triplet at roughly twice the
energy of the lowest 2
triplet at roughly twice the
energy of the lowest 2 excited state. But these more
excited state. But these more
macroscopic
nuclei also show a nice 0 , 2
, 2 ,
3
,
3 , 4
, 4 , 6
, 6 quintuplet at very roughly three times the energy
of the lowest 2
quintuplet at very roughly three times the energy
of the lowest 2 state. Yes, three identical phonons of spin 2 can
have a combined spin of 0, 2, 3, 4, and 6, but not 1 or 5
(c.f. 12.2).
state. Yes, three identical phonons of spin 2 can
have a combined spin of 0, 2, 3, 4, and 6, but not 1 or 5
(c.f. 12.2).
As subsection 14.13.1 showed, liquid drops can also vibrate
according to spherical harmonics 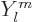 for
for 
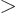 2. The lowest such
possibility
2. The lowest such
possibility 
 3 has spin 3 and negative parity. Vibration of this
type is called “octupole vibration,” while
3 has spin 3 and negative parity. Vibration of this
type is called “octupole vibration,” while 
 2 is referred to as “quadrupole vibration.” For very light nuclei, the energy of
octupole vibration is about twice that of the quadrupole type. That
would put the 3
2 is referred to as “quadrupole vibration.” For very light nuclei, the energy of
octupole vibration is about twice that of the quadrupole type. That
would put the 3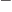 octupole vibration right in the middle of the
two-phonon quadrupole triplet. However, for heavier nuclei the 3
octupole vibration right in the middle of the
two-phonon quadrupole triplet. However, for heavier nuclei the 3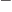 state will be relatively higher, since the energy reduction due to the
Coulomb term is relatively smaller in the case
state will be relatively higher, since the energy reduction due to the
Coulomb term is relatively smaller in the case 
 3. Indeed, the
first 3
3. Indeed, the
first 3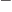 states for tellurium-120 and ruthenium-104 are found well
above the quadrupole quintuplet. The lowest 3
states for tellurium-120 and ruthenium-104 are found well
above the quadrupole quintuplet. The lowest 3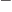 state for much
lighter oxygen-18 is relatively lower.
state for much
lighter oxygen-18 is relatively lower.
14.13.3 Draft: Nonspherical nuclei
The classical liquid drop model predicts that the nucleus cannot
maintain a spherical ground state if the destabilizing Coulomb energy
exceeds the stabilizing nuclear surface tension. Indeed, from
electromagnetic measurements, it is seen that many very heavy nuclei
do acquire a permanent nonspherical shape. These are called “deformed nuclei”.
They are roughly the red squares and yellow squares marked with
R
in figure 14.22. Near the stable line,
their mass number ranges are from about 150 to 190 and above 220.
But many unstable much lighter nuclei are deformed too.
The liquid drop model, in particular (14.19), predicts that
the nuclear shape becomes unstable at
If that was true, essentially all nuclei would be spherical. A mass
number of 150 corresponds to about 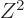

 equal to 26. However, as
pointed out in subsection 14.13.1, the liquid drop model
overestimates the stability with respect to relatively small
deformations. However, it does a fairly good job of explaining the
stability with respect to large ones. That explains why the
deformation of the deformed nuclei does not progress until they have
fissioned into pieces.
equal to 26. However, as
pointed out in subsection 14.13.1, the liquid drop model
overestimates the stability with respect to relatively small
deformations. However, it does a fairly good job of explaining the
stability with respect to large ones. That explains why the
deformation of the deformed nuclei does not progress until they have
fissioned into pieces.
Physicists have found that most deformed nuclei can be modeled well as
spheroids, i.e. ellipsoids of revolution. The nucleus is no longer
assumed to be spherically symmetric, but still axially symmetric.
Compared to spherical nuclei, there is now an additional
nondimensional number that will affect the various properties: the
ratio of the lengths of the two principal axes of the spheroid. That
complicates analysis. A single theoretical number now becomes an
entire set of numbers, depending on the value of the nondimensional
parameter. For some nuclei furthermore, axial symmetry is
insufficient and a model of an ellipsoid with three unequal axes is
needed. In that case there are two nondimensional parameters. Things
get much messier still then.
14.13.4 Draft: Rotational bands
Vibration is not the only semi-classical collective motion that nuclei
can perform. Deformed nuclei can also rotate as a whole. This
section gives a simplified semi-classical description of it.
14.13.4.1 Draft: Basic notions in nuclear rotation
Classically speaking, the kinetic energy of a solid body due to
rotation around an axis is 

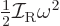 , where
, where 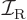 is the moment of inertia
around the axis and
is the moment of inertia
around the axis and 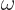 the angular velocity. Quantum mechanics
does not use angular velocity but angular momentum
the angular velocity. Quantum mechanics
does not use angular velocity but angular momentum 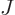

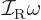 , and in these terms the kinetic energy is
, and in these terms the kinetic energy is


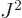

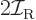 . Also, the square angular
momentum
. Also, the square angular
momentum 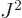 of a nucleus is quantized to be
of a nucleus is quantized to be 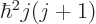 where
where
 is the net
is the net spin
of the nucleus, i.e. the azimuthal
quantum number of its net angular momentum.
Therefore, the kinetic energy of a nucleus due to its overall rotation
becomes:
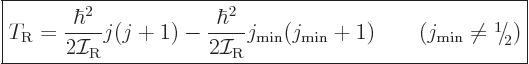 |
(14.23) |
Here 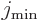 is the azimuthal quantum number of the “intrinsic state” in which the nucleus is not rotating as a
whole. The angular momentum of this state is in the individual
nucleons and not available for nuclear rotation, so it must be
subtracted. The total energy of a state with spin
is the azimuthal quantum number of the “intrinsic state” in which the nucleus is not rotating as a
whole. The angular momentum of this state is in the individual
nucleons and not available for nuclear rotation, so it must be
subtracted. The total energy of a state with spin  is then
is then
where  is the energy of the intrinsic state.
is the energy of the intrinsic state.
Figure 14.24:
Rotational bands of
hafnium-177.
[pdf]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
% vertical spacing 137...
...\frac{29}{2}}$}}
\put(400,4){\makebox(0,0)[bl]{?}}
\end{picture}
\end{figure}](img3255.gif) |
Consider now first a rough ballpark of the energies involved. Since
 is integer or half integer, the rotational energy comes in
discrete amounts of
is integer or half integer, the rotational energy comes in
discrete amounts of 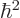

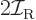 . The classical value for
the moment of inertia
. The classical value for
the moment of inertia 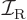 of a rigid sphere of mass
of a rigid sphere of mass  and radius
and radius
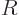 is
is 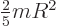 . For a nucleus the mass
. For a nucleus the mass  is about
is about  times the proton mass and the nuclear radius is given by
(14.9). Plugging in the numbers, the ballpark for
rotational energies becomes
times the proton mass and the nuclear radius is given by
(14.9). Plugging in the numbers, the ballpark for
rotational energies becomes
For a typical nonspherical nucleus like hafnium-177 in figure
14.24, taking the intrinsic state to be the ground
state with 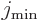 equal to
equal to 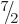 , the state
, the state 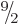 with an
additional unit of spin due to nuclear rotation would have a kinetic
energy of about 0.06 MeV. The lowest excited state is indeed a
with an
additional unit of spin due to nuclear rotation would have a kinetic
energy of about 0.06 MeV. The lowest excited state is indeed a 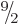 one, but its energy above the ground state is about twice 0.06 MeV. A
nucleus is not at all like a rigid body in classical mechanics. It
has already been pointed out in the subsection on nuclear vibrations
that in many ways a nucleus is much like a classical fluid. Still, it
remains true that rotational energies are small compared to typical
single-nucleon excitation energies. Therefore rotational effects must
be included if the low-energy excited states are to be understood.
one, but its energy above the ground state is about twice 0.06 MeV. A
nucleus is not at all like a rigid body in classical mechanics. It
has already been pointed out in the subsection on nuclear vibrations
that in many ways a nucleus is much like a classical fluid. Still, it
remains true that rotational energies are small compared to typical
single-nucleon excitation energies. Therefore rotational effects must
be included if the low-energy excited states are to be understood.
To better understand the discrepancy in kinetic energy, drop the
dubious assumption that the nuclear material is a rigid solid.
Picture the nucleus instead as a spheroid shape rotating around an
axis normal to the axis of symmetry. As far as the individual
nucleons are concerned, this shape is standing still because the
nucleons are going so much faster than the nuclear shape. A typical
nucleon has a kinetic energy in the order of 20 MeV, not a tenth of a
MeV, and it is so much lighter than the entire nucleus to boot. Still,
on the larger time scale of the nuclear rotations, the nucleons do
follow the overall motion of the nuclear shape, compare chapter
7.1.5. To describe this, consider the nuclear substance
to be an ideal liquid, one without internal viscosity. Without
viscosity, the nuclear liquid will not pick up the overall rotation of
the nuclear shape, so if the nuclear shape is spherical, the nuclear
liquid will not be affected at all. This reflect the fact that
Nuclear rotations can only be observed in nuclei with a nonspherical
equilibrium state, [31, p. 142].
But if the rotating nuclear shape is not spherical, the nuclear liquid
cannot be at rest. Then it will still have to move radially inwards
or outwards to follow the changing nuclear surface radius at a given
angular position. This will involve some angular motion too, but it
will remain limited. (Technically speaking, the motion will remain
irrotational, which means that the curl of the velocity field will
remain zero.) In the liquid picture, the moment of inertia has no
physical meaning and is simply defined by the relation


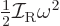 , with
, with  the
kinetic energy of the liquid. If typical numbers are plugged into
this picture, [31, p. 145], you find that the predicted
rotational energies are now too high. Therefore the conclusion must
be that the nuclear substance behaves like something in between a
solid and an ideal liquid, at least as far as nuclear rotations are
concerned. Fairly good values for the moment of inertia can be
computed by modeling the nucleon pairing effect using a superfluid
model, [40, pp. 493ff]
the
kinetic energy of the liquid. If typical numbers are plugged into
this picture, [31, p. 145], you find that the predicted
rotational energies are now too high. Therefore the conclusion must
be that the nuclear substance behaves like something in between a
solid and an ideal liquid, at least as far as nuclear rotations are
concerned. Fairly good values for the moment of inertia can be
computed by modeling the nucleon pairing effect using a superfluid
model, [40, pp. 493ff]
14.13.4.2 Draft: Basic rotational bands
Consider the spectrum of the deformed nucleus hafnium-177 in figure
14.24. At first the spectrum seems a mess. However,
take the ground state to be an intrinsic state
with a
spin 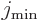 equal to
equal to 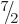 . Then you would expect that
there would also be energy levels with the nucleus still in the same
state but additionally rotating as a whole. Since quantum mechanics
requires that
. Then you would expect that
there would also be energy levels with the nucleus still in the same
state but additionally rotating as a whole. Since quantum mechanics
requires that  increases in integer steps, the rotating versions of
the ground state should have spin
increases in integer steps, the rotating versions of
the ground state should have spin  equal to any one of
equal to any one of 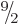 ,
,
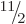 ,
, 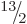 , ... And indeed, a sequence of
such excited states can be identified in the spectrum, as shown in the
top right of figure 14.24. Such a sequence of energy
states is called a “rotational band.” Note that all states in the band have the
same parity. That is exactly what you would expect based on the
classical picture of a rotating nucleus: the parity operator is a
purely spatial one, so mere rotation of the nucleus in time should not
change it.
, ... And indeed, a sequence of
such excited states can be identified in the spectrum, as shown in the
top right of figure 14.24. Such a sequence of energy
states is called a “rotational band.” Note that all states in the band have the
same parity. That is exactly what you would expect based on the
classical picture of a rotating nucleus: the parity operator is a
purely spatial one, so mere rotation of the nucleus in time should not
change it.
How about quantitative agreement with the predicted kinetic energies
of rotation (14.23)? Well, as seen in the previous
subsubsection, the effective moment of inertia is hard to find
theoretically. However, it can be computed from the measured energy
of the 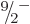 rotating state relative to the
rotating state relative to the 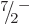 ground state using
(14.23). That produces a moment of inertia equal to 49% of
the corresponding solid sphere value. Then that value can be used to
compute the energies of the
ground state using
(14.23). That produces a moment of inertia equal to 49% of
the corresponding solid sphere value. Then that value can be used to
compute the energies of the 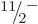 ,
, 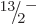 , ...states, using
again (14.23). The energies obtained in this way are
indicated by the spin-colored tick marks on the axis in the top-right
graph of figure 14.24. The lower energies agree very
well with the experimental values. Of course, the agreement of the
, ...states, using
again (14.23). The energies obtained in this way are
indicated by the spin-colored tick marks on the axis in the top-right
graph of figure 14.24. The lower energies agree very
well with the experimental values. Of course, the agreement of the
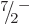 and
and 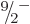 levels is automatic, but that of the higher levels
is not.
levels is automatic, but that of the higher levels
is not.
For example, the predicted energy of the 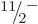 state is 0.251 MeV,
and the experimental value is 0.250 MeV. That is just a fraction of a
percent error, which is very much nontrivial. For higher rotational
energies, the experimental energies do gradually become somewhat lower
than predicted, but nothing major. There are many effects that could
explain the lowering, but an important one is “centrifugal stretching.” As noted, a nucleus is not really a
rigid body, and under the centrifugal forces of rapid rotation, it can
stretch a bit. This increases the effective moment of inertia and
hence lowers the kinetic energy, (14.23).
state is 0.251 MeV,
and the experimental value is 0.250 MeV. That is just a fraction of a
percent error, which is very much nontrivial. For higher rotational
energies, the experimental energies do gradually become somewhat lower
than predicted, but nothing major. There are many effects that could
explain the lowering, but an important one is “centrifugal stretching.” As noted, a nucleus is not really a
rigid body, and under the centrifugal forces of rapid rotation, it can
stretch a bit. This increases the effective moment of inertia and
hence lowers the kinetic energy, (14.23).
How about all these other excited energy levels of hafnium-177? Well,
first consider the nature of the ground state. Since hafnium-177 does
not have a spherical shape, the normal shell model does not apply to
it. In particular, the normal shell model would have the
hafnium-177’s odd neutron alone in the 6f subshell;
therefore it offers no logical way to explain the
subshell;
therefore it offers no logical way to explain the 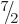 ground state
spin. However, the Schrödinger equation can solved using a nonspherical,
but still axially symmetric, potential to find suitable single
particle states. Using such states, it turns out that the final odd
neutron goes into a state with magnetic quantum number
ground state
spin. However, the Schrödinger equation can solved using a nonspherical,
but still axially symmetric, potential to find suitable single
particle states. Using such states, it turns out that the final odd
neutron goes into a state with magnetic quantum number 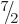 2 around
the nuclear axis and odd parity. (For a nonspherical potential, the
square angular momentum no longer commutes with the Hamiltonian and
both
2 around
the nuclear axis and odd parity. (For a nonspherical potential, the
square angular momentum no longer commutes with the Hamiltonian and
both  and
and  become uncertain.) With rotation, or better, with
uncertainty in axial orientation, this state gives rise to the
become uncertain.) With rotation, or better, with
uncertainty in axial orientation, this state gives rise to the 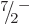 ground state of definite nuclear spin
ground state of definite nuclear spin  . Increasing angular
momentum then gives rise to the
. Increasing angular
momentum then gives rise to the 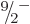 ,
, 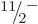 ,
, 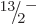 , ...
rotational band build on this ground state.
, ...
rotational band build on this ground state.
It is found that the next higher single-particle state has magnetic
quantum number 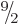 and even parity. If the odd neutron is kicked
into that state, it produces a low-energy
and even parity. If the odd neutron is kicked
into that state, it produces a low-energy 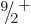 excited nuclear
state. Adding rotational motion to this intrinsic state produces the
excited nuclear
state. Adding rotational motion to this intrinsic state produces the
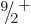 ,
, 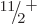 ,
, 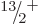 , ...rotational band shown in the
middle left of figure 14.24. (Note that for this
band, the experimental energies are larger than predicted.
Centrifugal stretching is certainly not the only effect causing
deviations from the simple theory.) In this case, the estimated
moment of inertia is about 64% of the solid sphere value. There is
no reason to assume that the moment of inertia remains the same if the
intrinsic state of the nucleus changes. However, clearly the value
must remain sensible.
, ...rotational band shown in the
middle left of figure 14.24. (Note that for this
band, the experimental energies are larger than predicted.
Centrifugal stretching is certainly not the only effect causing
deviations from the simple theory.) In this case, the estimated
moment of inertia is about 64% of the solid sphere value. There is
no reason to assume that the moment of inertia remains the same if the
intrinsic state of the nucleus changes. However, clearly the value
must remain sensible.
The low-lying 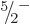 state is believed to be a result of promotion,
where a neutron from a
state is believed to be a result of promotion,
where a neutron from a 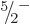 single-particle state is kicked up to
the
single-particle state is kicked up to
the 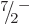 state where it can pair up with the 105th neutron already
there. Its rotating versions give rise to the rotational band in the
middle right of figure 14.24. The moment of inertia
is about 45% of the solid sphere value. The last two bands have
moments of inertia of 54% and 46%, in the expected ballpark.
state where it can pair up with the 105th neutron already
there. Its rotating versions give rise to the rotational band in the
middle right of figure 14.24. The moment of inertia
is about 45% of the solid sphere value. The last two bands have
moments of inertia of 54% and 46%, in the expected ballpark.
The general approach as outlined above has been extraordinarily
successful in explaining the excited states of deformed nuclei,
[31, p. 156].
14.13.4.3 Draft: Bands with intrinsic spin one-half
The semi-classical explanation of rotational bands was very
simplistic. While it works fine if the intrinsic spin of the rotating
nuclear state is at least one, it develops problems if it becomes
one-half or zero. The most tricky case is spin one-half.
Despite less than stellar results in the past, the discussion of the
problem will stick with a semi-classical approach. Recall first that
angular momentum is a vector. In vector terms, the total angular
momentum of the nucleus consists of rotational angular momentum and
intrinsic angular momentum of the nonrotating nucleus:
Now in the expression for rotational energy, (14.23) it was
implicitly assumed that the square angular momentum of the nucleus is
the sum of the square angular momentum of rotation plus the square
angular momentum of the intrinsic state. But classically the
Pythagorean theorem shows that this is only true if the two angular
momentum vectors are orthogonal.
Indeed, a more careful quantum treatment,
[40, pp. 356-389], gives rise to a
semi-classical picture in which the axis of the rotation is normal to
the axis of symmetry of the nucleus. In terms of the inviscid liquid
model of subsubsection 14.13.4.1, rotation about an axis of
symmetry does not do anything.
That leaves only the
intrinsic angular momentum for the component of angular momentum along
the axis of symmetry. The magnetic quantum number of this component
is 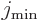 , equal to the spin of the intrinsic state.
Correct that: the direction of the axis of symmetry should not make a
difference. Therefore, the complete wave function should be an equal
combination of a state
, equal to the spin of the intrinsic state.
Correct that: the direction of the axis of symmetry should not make a
difference. Therefore, the complete wave function should be an equal
combination of a state 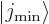 with magnetic quantum
number
with magnetic quantum
number 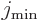 along the axis and a state
along the axis and a state  with magnetic quantum
with magnetic quantum 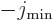 .
.
Next, the kinetic energy of rotation is, since 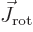

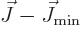 ,
,
As long as the middle term in the right hand side averages away, the
normal formula (14.23) for the energy of the rotational states
is fine. This happens if there is no correlation between the angular
momentum vectors 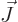 and
and 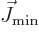 , because
then opposite and parallel alignments will cancel each other.
, because
then opposite and parallel alignments will cancel each other.
But not too quick. There is an obvious correlation since the axial
components are equal. The term can be written out in components to
give
where the  -axis is taken as the axis of symmetry of the nucleus.
Now think of these components as quantum operators. The
-axis is taken as the axis of symmetry of the nucleus.
Now think of these components as quantum operators. The
 components are no problem: since the magnetic quantum number is
constant along the axis, this term will just shift the all energy
levels in the band by the same amount, leaving the spacings between
energy levels the same.
components are no problem: since the magnetic quantum number is
constant along the axis, this term will just shift the all energy
levels in the band by the same amount, leaving the spacings between
energy levels the same.
However, the  and
and  components have the effect of turning a state
components have the effect of turning a state
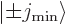 into some combination of states
into some combination of states
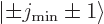 , chapter 12.11. Since
there is no rotational momentum in the axial direction,
, chapter 12.11. Since
there is no rotational momentum in the axial direction, 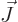 and
and
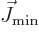 have quite similar effects on the wave function,
but it is not the same, for one because
have quite similar effects on the wave function,
but it is not the same, for one because 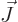
sees
the complete nuclear momentum. If 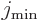 is 1 or more, the
effects remain inconsequential: then the produced states are part of a
different vibrational band, with different energies. A bit of
interaction between states of different energy is usually not a big
deal, chapter 5.3. But if
is 1 or more, the
effects remain inconsequential: then the produced states are part of a
different vibrational band, with different energies. A bit of
interaction between states of different energy is usually not a big
deal, chapter 5.3. But if 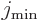

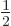 then
then 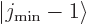 and
and 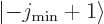 are part of
the state itself. In that case, the
are part of
the state itself. In that case, the  and
and  components of the
components of the
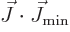 term produces a contribution to the
energy that does not average out, and the larger
term produces a contribution to the
energy that does not average out, and the larger  is, the
larger the contribution.
is, the
larger the contribution.
The expression for the kinetic energy of nuclear rotation then becomes
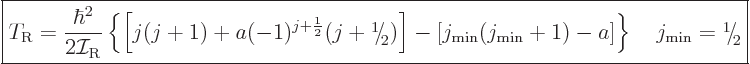 |
(14.24) |
where 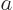 is a constant. Note that the additional term is
alternatingly positive and negative. Averaged over the entire
rotational band, the additional term does still pretty much vanish.
is a constant. Note that the additional term is
alternatingly positive and negative. Averaged over the entire
rotational band, the additional term does still pretty much vanish.
Figure 14.25:
Ground
state rotational band of tungsten-183.
[pdf]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
% vertical spacing 137...
...\frac{29}{2}}$}}
\put(400,4){\makebox(0,0)[bl]{?}}
\end{picture}
\end{figure}](img3276.gif) |
As an example, consider the  ground state rotational band of
tungsten-183, figure 14.25. To compute the rotational
kinetic energies in the band using (14.24) requires the
values of both
ground state rotational band of
tungsten-183, figure 14.25. To compute the rotational
kinetic energies in the band using (14.24) requires the
values of both 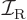 and
and  . The measured energies of the
. The measured energies of the
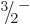 and
and 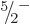 states above the ground state can be used to do so.
That produces a moment of inertia equal to 45% of the solid sphere
value and a nondimensional constant
states above the ground state can be used to do so.
That produces a moment of inertia equal to 45% of the solid sphere
value and a nondimensional constant 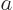 equal to 0.19. Next then the
formula can be used to predict the energies of the remaining states in
the band. As the axial tick marks in the right graph of figure
14.25 show, the prediction is quite good. Note in
particular that the energy interval between the
equal to 0.19. Next then the
formula can be used to predict the energies of the remaining states in
the band. As the axial tick marks in the right graph of figure
14.25 show, the prediction is quite good. Note in
particular that the energy interval between the 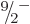 and
and 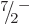 states is less than that between the
states is less than that between the 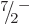 and
and 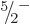 states.
Without the alternating term, there would be no way to explain that.
states.
Without the alternating term, there would be no way to explain that.
Figure 14.26:
Rotational bands of
aluminum-25.
[pdf]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
% vertical spacing 137...
...\frac{29}{2}}$}}
\put(400,4){\makebox(0,0)[bl]{?}}
\end{picture}
\end{figure}](img3277.gif) |
Much larger values of 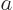 are observed for lighter nuclei. As an
example, consider aluminum-25 in figure 14.26. This
nucleus has been studied in detail, and a number of bands with an
intrinsic spin 1/2 have been identified. Particularly interesting is
the
are observed for lighter nuclei. As an
example, consider aluminum-25 in figure 14.26. This
nucleus has been studied in detail, and a number of bands with an
intrinsic spin 1/2 have been identified. Particularly interesting is
the  band in the bottom left of figure 14.26. For
this band
band in the bottom left of figure 14.26. For
this band 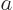

 3.2, and that is big enough to change the order of the
states in the band! For this nucleus, the moments of inertia are
70%, 96%, 107%, 141% and 207% respectively of the solid sphere
value.
3.2, and that is big enough to change the order of the
states in the band! For this nucleus, the moments of inertia are
70%, 96%, 107%, 141% and 207% respectively of the solid sphere
value.
14.13.4.4 Draft: Bands with intrinsic spin zero
The case that the intrinsic state has spin zero is particularly
important, because all even-even nuclei have a 0 ground state.
For bands build on a zero-spin intrinsic state, the thing to remember
is that the only values in the band are even spin and even parity:
0
ground state.
For bands build on a zero-spin intrinsic state, the thing to remember
is that the only values in the band are even spin and even parity:
0 , 2
, 2 , 4
, 4 , ...
, ...
This can be thought of as a consequence of the fact that the
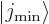 and
and  states of the previous
subsubsection become equal. Their odd or even combinations must be
constrained to prevent them from canceling each other.
states of the previous
subsubsection become equal. Their odd or even combinations must be
constrained to prevent them from canceling each other.
Figure 14.27:
Rotational bands of
erbium-164.
[pdf]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
% vertical spacing 137...
...\frac{29}{2}}$}}
\put(400,4){\makebox(0,0)[bl]{?}}
\end{picture}
\end{figure}](img3278.gif) |
As an example, consider erbium-164. The ground state band in the top
right of figure 14.27 consists of the states 0 ,
2
,
2 , 4
, 4 , ...as expected. The energies initially agree well
with the theoretical prediction (14.23) shown as tick marks.
For example, the prediction for the 4
, ...as expected. The energies initially agree well
with the theoretical prediction (14.23) shown as tick marks.
For example, the prediction for the 4 level has less than 2%
error. Deviations from theory show up at higher angular momenta,
which may have to do with centrifugal stretching.
level has less than 2%
error. Deviations from theory show up at higher angular momenta,
which may have to do with centrifugal stretching.
Other bands have been identified that are build upon vibrational
intrinsic states. (A 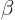 or beta vibration maintains the assumed
intrinsic axial symmetry of the nucleus, a
or beta vibration maintains the assumed
intrinsic axial symmetry of the nucleus, a 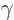 or gamma one does
not.) Their energy spacings follow (14.23) again well. The
moments of inertia are 46%, 49% and 61% of the solid sphere value.
or gamma one does
not.) Their energy spacings follow (14.23) again well. The
moments of inertia are 46%, 49% and 61% of the solid sphere value.
Figure 14.28:
Ground
state rotational band of magnesium-24.
[pdf]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
% vertical spacing 137...
...\frac{29}{2}}$}}
\put(400,4){\makebox(0,0)[bl]{?}}
\end{picture}
\end{figure}](img3279.gif) |
Light even-even nuclei can also be deformed and show rotational bands.
As an example, figure 14.28 shows the ground state band
of magnesium-24. The moment of inertia is 75% of the solid sphere
value.
It may also be mentioned that nuclei with intrinsic spin zero combined
with an octupole vibration can give rise to bands that are purely odd
spin/odd parity ones, 1 , 3
, 3 , 5
, 5 , ...,
[40, p. 368]. The lowest odd parity states
for erbium-164 are 1
, ...,
[40, p. 368]. The lowest odd parity states
for erbium-164 are 1 and 3
and 3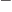 ones, with no 2
ones, with no 2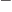 state in
between, for a really high estimated moment of inertia of 148%, and a
potential 5
state in
between, for a really high estimated moment of inertia of 148%, and a
potential 5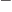 state at roughly, but not accurately, the predicted
position. Anomalous bands that have the parity inverted may also be
possible; hafnium-176 is believed to have a couple of excited states
like that, 0
state at roughly, but not accurately, the predicted
position. Anomalous bands that have the parity inverted may also be
possible; hafnium-176 is believed to have a couple of excited states
like that, 0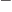 at 1.819 MeV and 2
at 1.819 MeV and 2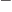 at 1.857 MeV, with a moment of
inertia of 98%.
at 1.857 MeV, with a moment of
inertia of 98%.
Centrifugal effects can be severe enough to change the internal
structure of the nucleus nontrivially. Typically, zero-spin pairings
between nucleons may be broken up, allowing the nucleons to start
rotating along with the nucleus. That creates a new band build on the
changed intrinsic state. Physicists then define the state of lowest
energy at a given angular momentum as the “yrast state.” The term is not an acronym, but Swedish for
that what rotates more.
For a discussion, a book for
specialists will need to be consulted.
14.13.4.5 Draft: Even-even nuclei
All nuclei with even numbers of both protons and neutrons have a 0 ground state. For nonspherical ones, the rotational model predicts a
ground state band of low-lying 2
ground state. For nonspherical ones, the rotational model predicts a
ground state band of low-lying 2 , 4
, 4 , 6
, 6 , ...states.
The ratio of the energy levels of the 4
, ...states.
The ratio of the energy levels of the 4 and 2
and 2 states is given
by (14.23)
states is given
by (14.23)
For spherical nuclei, the vibrational model also predicts a 2 lowest excited state, but the 4
lowest excited state, but the 4 excited state is now part of a
triplet, and the triplet has only twice the energy of the 2
excited state is now part of a
triplet, and the triplet has only twice the energy of the 2 state.
Therefore, if the ratio of the energy of the second excited state to
the lowest 2
state.
Therefore, if the ratio of the energy of the second excited state to
the lowest 2 state is plotted, as done in figure 14.22,
then vibrating nuclei should be indicated by a value 2 (green) and
rotating nuclei by a value 3.33 (red). If the figure is examined, it
may be open to some doubt whether green squares are necessarily
vibrational, but the red squares quite nicely locate the rotational
ones.
state is plotted, as done in figure 14.22,
then vibrating nuclei should be indicated by a value 2 (green) and
rotating nuclei by a value 3.33 (red). If the figure is examined, it
may be open to some doubt whether green squares are necessarily
vibrational, but the red squares quite nicely locate the rotational
ones.
In the figure, nuclei marked with V
have 0 , 2
, 2 ,
and a 0
,
and a 0 , 2
, 2 , 4
, 4 triplet as the lowest 5 energy states, the
triplet allowed to be in any order. Nuclei marked with an
triplet as the lowest 5 energy states, the
triplet allowed to be in any order. Nuclei marked with an
R
have the sequence 0 , 2
, 2 , 4
, 4 , and 6
, and 6 as
the lowest four energy states. Note that this criterion misses the
light rotational nuclei like magnesium-24; for light nuclei the
rotational energies are not small enough to be well separated from
shell effects. Near the stable line, rotating nuclei are found in the
approximate mass number ranges 20
as
the lowest four energy states. Note that this criterion misses the
light rotational nuclei like magnesium-24; for light nuclei the
rotational energies are not small enough to be well separated from
shell effects. Near the stable line, rotating nuclei are found in the
approximate mass number ranges 20 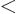

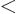 30, 150
30, 150 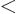

 190, and 220
190, and 220 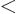
 . However, away from the stable
line rotating nuclei are also found at other mass numbers.
. However, away from the stable
line rotating nuclei are also found at other mass numbers.
14.13.4.6 Draft: Nonaxial nuclei
While most nuclei are well modeled as axially symmetric, some nuclei
are not. For such nuclei, an ellipsoidal model can be used with the
three major axes all off different length. There are now two
nondimensional axis ratios that characterize the nucleus, rather than
just one.
This additional nondimensional parameter makes the spectrum much more
complex. In particular, in addition to the normal rotational bands,
associated anomalous
secondary bands appear. The
first is a 2 , 3
, 3 , 4
, 4 , ...one, the second a 4
, ...one, the second a 4 , 5
, 5 ,
...one, etcetera. The energies in these bands are not independent,
but related to those in the primary band.
,
...one, etcetera. The energies in these bands are not independent,
but related to those in the primary band.
Figure 14.29:
Rotational bands of osmium-190.
[pdf]
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
% vertical spacing 137...
...\frac{29}{2}}$}}
\put(400,4){\makebox(0,0)[bl]{?}}
\end{picture}
\end{figure}](img3281.gif) |
Figure 14.29 shows an example. The primary ground
state band in the top right quickly develops big deviations from the
axially symmetric theory (14.23) values (thin tick marks.)
Computation using the ellipsoidal model for a suitable value of the
deviation from axial symmetry is much better (thick tick marks.) The
predicted energy levels of the first anomalous band also agree well
with the predicted values. The identification of the bands was taken
from [40, p. 416], but since they do not list
the energies of the second anomalous band, that value was taken from
[36, p. 388].
In the limit that the nuclear shape becomes axially symmetric, the
anomalous bands disappear towards infinite energy. In the limit that
the nuclear shape becomes spherical, all states in the primary bands
except the lowest one also disappear to infinity, assuming that the
moment of inertia
becomes zero as the ideal liquid
model says.
![]()
![]()
![]()
![]()
![]() .
.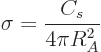
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
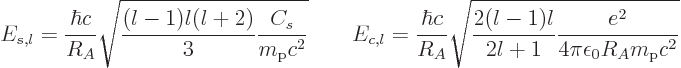
![]()
![]()
![]() ,
,![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
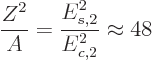
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 2
2![]()
![]()
![]()
![]() .
.![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 3
3![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
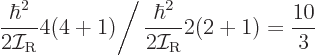
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,