The below are the simplest possible descriptions of various symbols,
just to help you keep reading if you do not remember/know what they
stand for. Don't cite them on a math test and then blame this book
for your grade.
Watch it. There are so many ad hoc usages of symbols, some will have
been overlooked here. Always use common sense first in guessing what
a symbol means in a given context.
The quoted values of physical constants are usually taken from NIST
CODATA in 2012 or later. The final digit of the listed value is
normally doubtful. (It corresponds to the first nonzero digit of the
standard deviation). Numbers ending in triple dots are exact and
could be written down to more digits than listed if needed.
-

- A dot might indicate
- A dot product between vectors, if in between them.
- A time derivative of a quantity, if on top of it.
And also many more prosaic things (punctuation signs, decimal points,
...).
- Multiplication symbol. May indicate:
- An emphatic multiplication.
- Multiplication continued on the next line or from the previous
line.
- A vectorial product between vectors. In index notation,
the
 -th component of
-th component of 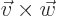 equals
equals
where 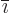 is the index following
is the index following  in the sequence
123123..., and
in the sequence
123123..., and 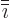 the one preceding it (or second
following). Alternatively, evaluate the determinant
the one preceding it (or second
following). Alternatively, evaluate the determinant
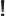
- Might be used to indicate a factorial. Example:
5!
 1
1  2
2  3
3  4
4  5
5  120.
120.
The function that generalizes 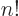 to noninteger values of
to noninteger values of 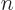 is
called the gamma function;
is
called the gamma function; 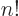

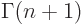 . The
gamma function generalization is due to, who else, Euler. (However,
the fact that
. The
gamma function generalization is due to, who else, Euler. (However,
the fact that 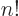

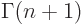 instead of
instead of 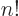

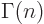 is due to the idiocy of Legendre.) In
Legendre-resistant notation,
is due to the idiocy of Legendre.) In
Legendre-resistant notation,
Straightforward integration shows that 0! is 1 as it should, and
integration by parts shows that 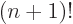

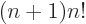 ,
which ensures that the integral also produces the correct value of
,
which ensures that the integral also produces the correct value of
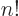 for any higher integer value of
for any higher integer value of 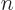 than 0. The integral,
however, exists for any real value of
than 0. The integral,
however, exists for any real value of 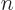 above
above  1, not just
integers. The values of the integral are always positive, tending to
positive infinity for both
1, not just
integers. The values of the integral are always positive, tending to
positive infinity for both 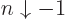 , (because the
integral then blows up at small values of
, (because the
integral then blows up at small values of 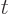 ), and for
), and for
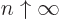 , (because the integral then blows up at
medium-large values of
, (because the integral then blows up at
medium-large values of 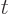 ). In particular, Stirling’s formula
says that for large positive
). In particular, Stirling’s formula
says that for large positive 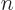 ,
, 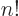 can be approximated as
can be approximated as
where the value indicated by the dots becomes negligibly small for
large 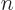 . The function
. The function 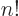 can be extended further to any
complex value of
can be extended further to any
complex value of 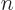 , except the negative integer values of
, except the negative integer values of
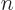 , where
, where 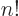 is infinite, but is then no longer positive.
Euler’s integral can be done for
is infinite, but is then no longer positive.
Euler’s integral can be done for 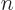

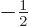 by making
the change of variables
by making
the change of variables 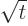

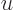 , producing the
integral
, producing the
integral 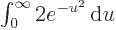 , or
, or
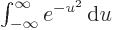 , which equals
, which equals
 and the integral under the square root can be done analytically
using polar coordinates. The result is that
and the integral under the square root can be done analytically
using polar coordinates. The result is that
To get 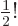 , multiply by
, multiply by 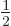 , since
, since 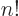

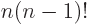 .
.
A double exclamation mark may mean every second item is skipped,
e.g. 5!!  1
1  3
3  5. In general,
5. In general, 

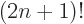 /
/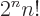 . Of course, 5!! should logically
mean (5!)!. Logic would indicate that 5
. Of course, 5!! should logically
mean (5!)!. Logic would indicate that 5  3
3  1
should be indicated by something like 5!’. But what is logic
in physics?
1
should be indicated by something like 5!’. But what is logic
in physics?
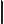
- May indicate:
- The magnitude or absolute value of the number or vector, if
enclosed between a pair of them.
- The determinant of a matrix, if enclosed between a pair of
them.
- The norm of the function, if enclosed between two pairs of them.
- The end of a bra or start of a ket.
- A visual separator in inner products.
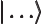
- A
ket
is used to
indicate some state. For example, 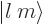 indicates an angular
momentum state with azimuthal quantum number
indicates an angular
momentum state with azimuthal quantum number 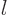 and magnetic
quantum number
and magnetic
quantum number 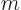 . Similarly,
. Similarly, 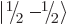 is the spin-down
state of a particle with spin
is the spin-down
state of a particle with spin 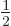 . Other common ones
are
. Other common ones
are 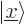 for the position eigenfunction
for the position eigenfunction 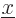 ,
i.e.
,
i.e. 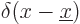 ,
, 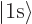 for the 1s or
for the 1s or
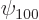 hydrogen state,
hydrogen state, 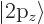 for the 2p
for the 2p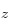 or
or
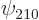 state, etcetera. In short, whatever can indicate some
state can be pushed into a ket.
state, etcetera. In short, whatever can indicate some
state can be pushed into a ket.
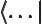
- A
bra
is like a ket
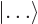 , but appears in the left side of inner products,
instead of the right one.
, but appears in the left side of inner products,
instead of the right one.
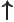
- Indicates the
spin up
state. Mathematically, equals the function 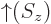 which is by
definition equal to 1 at
which is by
definition equal to 1 at 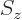

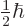 and equal to 0
at
and equal to 0
at 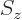

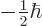 . A spatial wave function
multiplied by
. A spatial wave function
multiplied by 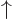 is a particle in that spatial state with
its spin up. For multiple particles, the spins are listed with
particle 1 first.
is a particle in that spatial state with
its spin up. For multiple particles, the spins are listed with
particle 1 first.
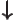
- Indicates the
spin down
state. Mathematically, equals the function 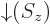 which is by
definition equal to 0 at
which is by
definition equal to 0 at 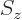

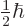 and equal to 1
at
and equal to 1
at 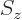

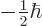 . A spatial wave function
multiplied by
. A spatial wave function
multiplied by 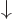 is a particle in that spatial state with
its spin down. For multiple particles, the spins are listed with
particle 1 first.
is a particle in that spatial state with
its spin down. For multiple particles, the spins are listed with
particle 1 first.
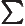
- Summation symbol. Example: if in three
dimensional space a vector
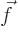 has components
has components 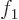
 2,
2,
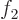
 1,
1, 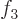
 4, then
4, then 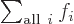 stands
for
stands
for 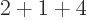
 7.
7.
One important thing to remember: the symbol used for the summation
index does not make a difference: 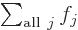 is
exactly the same as
is
exactly the same as 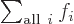 . So freely
rename the index, but always make sure that the new name is not
already used for something else in the part that it appears in. If
you use the same name for two different things, it becomes a mess.
. So freely
rename the index, but always make sure that the new name is not
already used for something else in the part that it appears in. If
you use the same name for two different things, it becomes a mess.
Related to that, 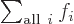 is not something
that depends on an index
is not something
that depends on an index  . It is just a combined simple
number. Like 7 in the example above. It is commonly said that the
summation index
. It is just a combined simple
number. Like 7 in the example above. It is commonly said that the
summation index sums away.
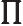
- (Not to be confused with
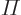 further
down.) Multiplication symbol. Example: if in three dimensional
space a vector
further
down.) Multiplication symbol. Example: if in three dimensional
space a vector 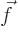 has components
has components 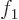
 2,
2, 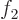
 1,
1, 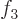
 4, then
4, then 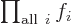 stands for
stands for
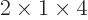
 6.
6.
One important thing to remember: the symbol used for the
multiplications index does not make a difference:
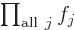 is exactly the same as
is exactly the same as
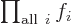 . So freely rename the index, but
always make sure that the new name is not already used for something
else in the part that it appears in. If you use the same name for
two different things, it becomes a mess.
. So freely rename the index, but
always make sure that the new name is not already used for something
else in the part that it appears in. If you use the same name for
two different things, it becomes a mess.
Related to that, 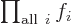 is not something
that depends on an index
is not something
that depends on an index  . It is just a combined simple
number. Like 6 in the example above. It is commonly said that the
multiplication index
. It is just a combined simple
number. Like 6 in the example above. It is commonly said that the
multiplication index factors away.
(By who?)
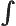
- Integration symbol, the continuous version of
the summation symbol. For example,
is the summation of 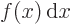 over all infinitesimally small
fragments
over all infinitesimally small
fragments 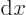 that make up the entire
that make up the entire  -range. For example,
-range. For example,
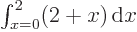 equals 3
equals 3  2
2  6; the average value of
6; the average value of
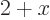 between
between 
 0 and
0 and 
 2 is 3, and the sum of all the
infinitesimally small segments
2 is 3, and the sum of all the
infinitesimally small segments 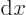 gives the total length
2 of the range in
gives the total length
2 of the range in  from 0 to 2.
from 0 to 2.
One important thing to remember: the symbol used for the integration
variable does not make a difference: 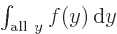 is exactly the same as
is exactly the same as 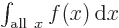 . So
freely rename the integration variable, but always make sure that
the new name is not already used for something else in the part it
appears in. If you use the same name for two different things, it
becomes a mess.
. So
freely rename the integration variable, but always make sure that
the new name is not already used for something else in the part it
appears in. If you use the same name for two different things, it
becomes a mess.
Related to that 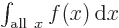 is not
something that depends on a variable
is not
something that depends on a variable  . It is just a
combined number. Like 6 in the example above. It is commonly said
that the integration variable
. It is just a
combined number. Like 6 in the example above. It is commonly said
that the integration variable integrates away.
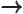
- May indicate:
- An approaching process.
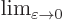 indicates
for practical purposes the value of the expression following the
indicates
for practical purposes the value of the expression following the
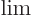 when
when 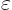 is extremely small. Similarly,
is extremely small. Similarly,
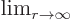 indicates the value of the following
expression when
indicates the value of the following
expression when 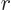 is extremely large.
is extremely large.
- The fact that the left side leads to, or implies, the right-hand
side.
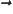
- Vector symbol. An arrow above a
letter indicates it is a vector. A vector is a quantity that
requires more than one number to be characterized. Typical vectors
in physics include position
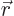 , velocity
, velocity  , linear
momentum
, linear
momentum 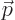 , acceleration
, acceleration 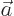 , force
, force 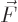 , angular
momentum
, angular
momentum 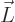 , etcetera.
, etcetera.
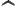
- A hat over a letter in this
book indicates that it is the operator, turning functions into other
functions.
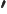
- May indicate:
- A derivative of a function. Examples:
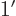
 0,
0, 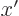
 1,
1, 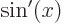

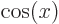 ,
, 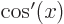

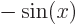 ,
, 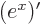

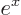 .
.
- A small or modified quantity.
- A quantity per unit length.

- The spatial differentiation operator
nabla. In Cartesian coordinates:
Nabla can be applied to a scalar function  in which case it gives
a vector of partial derivatives called the gradient of the
function:
in which case it gives
a vector of partial derivatives called the gradient of the
function:
Nabla can be applied to a vector in a dot product multiplication, in
which case it gives a scalar function called the divergence of the
vector:
or in index notation
Nabla can also be applied to a vector in a vectorial product
multiplication, in which case it gives a vector function called the curl or rot of the
vector. In index notation, the  -th component of this vector is
-th component of this vector is
where 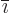 is the index following
is the index following  in the sequence 123123...,
and
in the sequence 123123...,
and 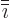 the one preceding it (or the second following it).
the one preceding it (or the second following it).
The operator  is called the Laplacian. In Cartesian coordinates:
is called the Laplacian. In Cartesian coordinates:
Sometimes the Laplacian is indicated as 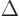 . In
relativistic index notation it is equal to
. In
relativistic index notation it is equal to
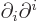 , with maybe a minus sign depending on
who you talk with.
, with maybe a minus sign depending on
who you talk with.
In non Cartesian coordinates, don’t guess; look these operators
up in a table book, [41, pp. 124-126]: . For example,
in spherical coordinates,
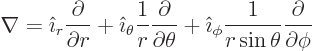 |
(N.2) |
That allows the gradient of a scalar function  ,
i.e.
,
i.e. 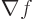 , to be found immediately. But if you apply
, to be found immediately. But if you apply
 on a vector, you have to be very careful because you also
need to differentiate
on a vector, you have to be very careful because you also
need to differentiate 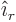 ,
, 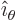 , and
, and
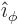 . In particular, the correct divergence of a
vector
. In particular, the correct divergence of a
vector  is
is
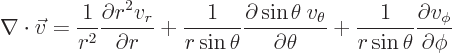 |
(N.3) |
The curl 

 of the vector is
of the vector is
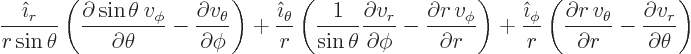 |
(N.4) |
Finally the Laplacian is:
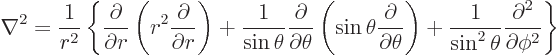 |
(N.5) |
See also spherical coordinates.
Cylindrical coordinates are usually indicated as 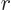 ,
, 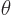 and
and  . Here
. Here  is the Cartesian coordinate, while
is the Cartesian coordinate, while 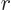 is
the distance from the
is
the distance from the  -axis and
-axis and 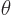 the angle around the
the angle around the  axis. In two dimensions, i.e. without the
axis. In two dimensions, i.e. without the  terms, they are
usually called polar coordinates. In cylindrical coordinates:
terms, they are
usually called polar coordinates. In cylindrical coordinates:
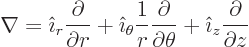 |
(N.6) |
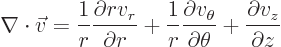 |
(N.7) |
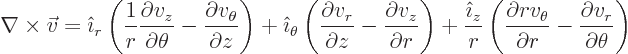 |
(N.8) |
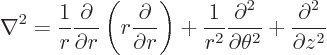 |
(N.9) |

- The
D'Alembertian is defined as
where 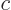 is a constant called the wave speed. In relativistic
index notation,
is a constant called the wave speed. In relativistic
index notation,  is equal to
is equal to 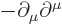 .
.
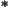
- A superscript star normally indicates a complex
conjugate. In the complex conjugate of a number, every
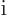 is
changed into a
is
changed into a  .
.
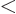
- Less than.
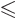
- Less than or equal.
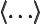
- May indicate:
- An inner product.
- An expectation value.
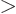
- Greater than.
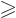
- Greater than or equal.
![$
\setbox 0=\hbox{$[\ldots]$}\kern-.025em\copy0\kern-\wd0 \kern.05em\copy0\kern-\wd0\kern-.025em\raise.0433em\box0 $](img7969.gif)
- May indicate:
- A grouping of terms in a formula.
- A commutator. For example,
![$[A,B]$](img786.gif)

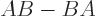 .
.

- Equals sign. The quantity to the left is the same as
the one to the right.

- Emphatic equals sign. Typically means “by
definition equal” or
everywhere equal.
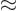
- Indicates approximately equal. Read it as “is
approximately equal to.”
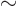
- Indicates approximately equal. Often used when the
approximation applies only when something is small or large. Read
it as
is approximately equal to
or as “is
asymptotically equal to.”
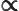
- Proportional to. The two sides are equal
except for some unknown constant factor.
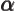
- (alpha) May indicate:
- The fine structure constant,
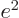 /
/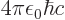 ,
equal to 7.297 352 570 10
,
equal to 7.297 352 570 10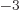 , or about 1/137, in value.
, or about 1/137, in value.
- A Dirac equation matrix.
- A nuclear decay mode in which a helium-4 nucleus is emitted.
- Internal conversion rate as fraction of the gamma decay rate.
- Some constant.
- Some angle.
- An eigenfunction of a generic operator
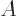 .
.
- A summation index.
- Component index of a vector.
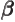
- (beta) May indicate:
- A nuclear decay mode in which an electron (
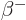 ) or
positron (
) or
positron (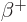 ) is emitted. Sometimes
) is emitted. Sometimes 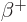 is taken to
also include electron capture.
is taken to
also include electron capture.
- A nuclear vibrational mode that maintains the axial symmetry
of the nucleus.
- Some constant.
- Some angle.
- An eigenfunction of a generic operator
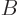 .
.
- A summation index.
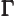
- (Gamma) May indicate:
- The Gamma function. Look under
!
for details.
- The
width
or uncertainty in energy of an
approximate energy eigenstate.
- Origin in wave number space.
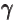
- (gamma) May indicate:
- Gyromagnetic ratio.
- Standard symbol for a photon of electromagnetic radiation.
- A nuclear de-excitation mode in which a photon is emitted.
- A nuclear vibrational mode that messes up the axial symmetry
of the nucleus.
- Summation index.
- Integral in the tunneling WKB approximation.

- (capital delta) May indicate:
- An increment in the quantity following it.
- A delta particle.
- Often used to indicate the Laplacian
 .
.
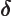
- (delta) May indicate:
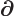
- (partial) Indicates a vanishingly small
change or interval of the following variable. For example,
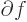 /
/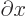 is the ratio of a vanishingly small
change in function
is the ratio of a vanishingly small
change in function  divided by the vanishingly small change in
variable
divided by the vanishingly small change in
variable  that causes this change in
that causes this change in  . Such ratios define
derivatives, in this case the partial derivative of
. Such ratios define
derivatives, in this case the partial derivative of  with respect
to
with respect
to  .
.
Also used in relativistic index notation, chapter
1.2.5.
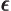
- (epsilon) May indicate:
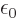 is the permittivity of space. Equal to
8.854 187 817... 10
is the permittivity of space. Equal to
8.854 187 817... 10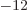 C
C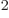 /J m. The exact value is
1
/J m. The exact value is
1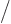
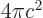 10
10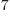 C
C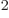 /J m, because of the exact SI
definitions of ampere and speed of light.
/J m, because of the exact SI
definitions of ampere and speed of light.
- Scaled energy.
- Orbital energy.
- Lagrangian multiplier.
- A small quantity, if symbol
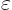 is not available.
is not available.
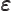
- (variant of epsilon) May indicate:
- A very small quantity.
- The slop in energy conservation during a decay process.
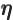
- (eta) May be used to indicate a
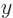 -position
of a particle.
-position
of a particle.
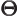
- (capital theta) Used in this book to
indicate some function of
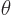 to be determined.
to be determined.
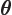
- (theta) May indicate:
- In spherical coordinates, the angle from the chosen
 axis, with
apex at the origin.
axis, with
apex at the origin.
 -position of a particle.
-position of a particle.
- A generic angle, like the one between the vectors in a
cross or dot product.
- Integral acting as an angle in the classical WKB
approximation.
- Integral acting as an angle in the adiabatic approximation.
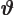
- (variant of theta) An alternate symbol
for
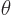 .
.
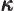
- (kappa) May indicate:
- A constant that physically corresponds to some wave number.
- A summation index.
- Thermal conductivity.
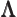
- (Lambda) May indicate:
- Lorentz transformation matrix.
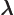
- (lambda) May indicate:
- Wave length.
- Decay constant.
- A generic eigenvalue.
- Entry of a Lorentz transformation.
- Scaled square momentum.
- Some multiple of something.
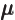
- (mu) May indicate:
- Magnetic dipole moment:
Alpha particle: 0 (spin is zero).
Deuteron: 0.433 073 49 10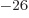 J/T or 0.857 438 231
J/T or 0.857 438 231 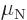 .
.
Electron:  9.284 764 3 10
9.284 764 3 10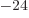 J/T or
J/T or
 1.001 159 652 180 8
1.001 159 652 180 8 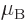 .
.
Helion:  1.074 617 49 10
1.074 617 49 10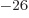 J/T or
J/T or  2.127 625 306
2.127 625 306 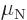 .
.
Neutron:  0.966 236 5 10
0.966 236 5 10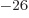 J/T or
J/T or  1.913 042 7
1.913 042 7 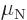 .
.
Proton: 1.410 606 74 10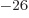 J/T or 2.792 847 36
J/T or 2.792 847 36 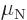 .
.
Triton: 1.504 609 45 10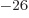 J/T or 2.978 962 45
J/T or 2.978 962 45 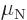 .
.
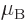

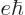 /
/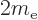
 9.274 009 7 10
9.274 009 7 10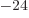 J/T
or 5.788 381 807 10
J/T
or 5.788 381 807 10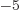 eV/T is the Bohr magneton.
eV/T is the Bohr magneton.
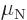

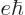 /
/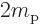
 5.050 783 5 10
5.050 783 5 10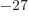 J/T
or 3.152 451 261 10
J/T
or 3.152 451 261 10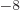 eV/T is the nuclear magneton.
eV/T is the nuclear magneton.
- A summation index.
- Chemical potential/molar Gibbs free energy.
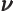
- (nu) May indicate:
- Electron neutrino.
- Scaled energy eigenfunction number in solids.
- A summation index.
- Strength of a delta function potential.
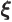
- (xi) May indicate:
- Scaled argument of the one-dimensional harmonic oscillator
eigenfunctions.
 -position of a particle.
-position of a particle.
- A summation or integration index.
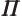
- (Oblique Pi) (Not to be confused with
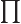 described higher up.) Parity operator. Replaces
described higher up.) Parity operator. Replaces 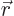 by
by
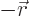 . That is equivalent to a mirroring in a mirror through the
origin, followed by a 180
. That is equivalent to a mirroring in a mirror through the
origin, followed by a 180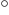 rotation around the axis
normal to the mirror.
rotation around the axis
normal to the mirror.
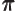
- (pi) May indicate:
- A constant with value
3.141 592 653 589 793 238 462....
The area of a circle of radius 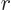 is
is 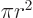 and its perimeter is
and its perimeter is 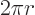 .
.
The volume of a sphere of radius 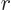 is
is 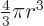 and its
surface is
and its
surface is 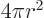 .
.
A 180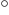 angle expressed in radians is
angle expressed in radians is 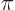 .
.
Note also that 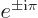

 1 and
1 and 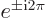
 1.
1.
- A chemical bond that looks from the side like a p state.
- A particle involved in the forces keeping the nuclei of atoms
together (
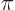 -meson or pion for short).
-meson or pion for short).
- Parity.
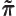
- Canonical momentum density.
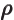
- (rho) May indicate:
- Electric charge per unit volume.
- Scaled radial coordinate.
- Radial coordinate.
- Eigenfunction of a rotation operator
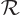 .
.
- Mass-base density.
- Energy density of electromagnetic radiation.
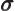
- (sigma) May indicate:
- A standard deviation of a value.
- A chemical bond that looks like an s state when seen from the
side.
- Pauli spin matrix.
- Surface tension.
- Electrical conductivity.
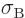
 5.670 37 W/m
5.670 37 W/m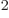 K
K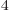 is
the Stefan-Boltzmann
is
the Stefan-Boltzmann
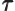
- (tau) May indicate:
- A time or time interval.
- Life time or half life.
- Some coefficient.
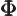
- (capital phi) May indicate:
- Some function of
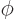 to be determined.
to be determined.
- The momentum-space wave function.
- Relativistic electromagnetic potential.
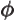
- (phi) May indicate:
- In spherical coordinates, the angle around the chosen
 axis. Increasing
axis. Increasing 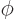 by
by 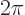 encircles the
encircles the  -axis exactly
once.
-axis exactly
once.
- A phase angle.
- Something equivalent to an angle.
- Field operator
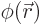 annihilates a particle at position
annihilates a particle at position
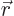 while
while 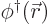 creates one at that position.
creates one at that position.
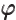
- (variant of phi) May indicate:
- A change in angle
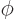 .
.
- An alternate symbol for
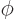 .
.
- An electrostatic potential.
- An electrostatic quantum field.
- A hypothetical selectostatic quantum field.
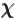
- (chi) May indicate
- Spinor component.
- Gauge function of electromagnetic field.
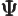
- (capital psi) Upper case psi is used for the
wave function.
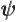
- (psi) Typically used to indicate an energy
eigenfunction. Depending on the system, indices may be added to
distinguish different ones. In some cases
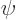 might be used
instead of
might be used
instead of 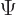 to indicate a system in an energy eigenstate. Let
me know and I will change it. A system in an energy eigenstate
should be written as
to indicate a system in an energy eigenstate. Let
me know and I will change it. A system in an energy eigenstate
should be written as 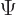

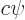 , not
, not 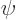 ,
with
,
with 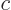 a constant of magnitude 1.
a constant of magnitude 1.
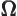
- (Omega) May indicate:
- Solid angle. See
angle
and “spherical
coordinates.”
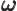
- (omega) May indicate:
- Angular frequency of the classical harmonic oscillator. Equal
to
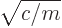 where
where 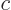 is the spring constant and
is the spring constant and 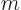 the mass.
the mass.
- Angular frequency of a system.
- Angular frequency of light waves.
- Perturbation frequency,
- Any quantity having units of frequency, 1/s.
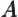
- May indicate:
- Repeatedly used to indicate the operator for a generic
physical quantity
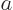 , with eigenfunctions
, with eigenfunctions 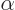 .
.
- Electromagnetic vector potential, or four vector potential.
- Einstein
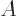 coefficient.
coefficient.
- Some generic matrix.
- Some constant.
- Area.
- Å
- Ångstrom. Equal to 10
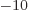 m.
m.
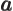
- May indicate:
- The value of a generic physical quantity with operator
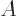
- The amplitude of the spin-up state
- The amplitude of the first state in a two-state system.
- Acceleration.
- Start point of an integration interval.
- The first of a pair of particles.
- Some coefficient.
- Some constant.
- Absorptivity of electromagnetic radiation.
- Annihilation operator
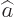 or creation operator
or creation operator 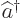 .
.
- Bohr radius of helium ion.
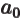
- May indicate:
- Bohr radius,
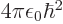 /
/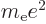 or
0.529 177 210 9 Å, with Å
or
0.529 177 210 9 Å, with Å 10
10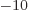 m. Comparable
in size to atoms, and a good size to use to simplify various
formulae.
m. Comparable
in size to atoms, and a good size to use to simplify various
formulae.
- The initial value of a coefficient
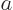 .
.
- absolute
- May indicate:
- The absolute value of a real number
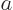 is indicated by
is indicated by  .
It equals
.
It equals 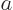 is
is 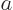 is positive or zero and
is positive or zero and 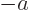 if
if 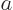 is
negative.
is
negative.
- The absolute value of a complex number
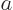 is indicated by
is indicated by
 . It equals the length of the number plotted as a vector in
the complex plane. This simplifies to above definition if
. It equals the length of the number plotted as a vector in
the complex plane. This simplifies to above definition if 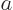 is
real.
is
real.
- An absolute temperature is a temperature measured from
absolute zero. At absolute zero all systems are in their ground
state. Absolute zero is
 273.15
273.15 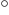 C in degrees
Centrigrade (Celsius). The SI absolute temperature scale is
degrees Kelvin, K. Absolute zero temperature is 0 K, while
0
C in degrees
Centrigrade (Celsius). The SI absolute temperature scale is
degrees Kelvin, K. Absolute zero temperature is 0 K, while
0 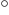 C is 273.15 K.
C is 273.15 K.
- adiabatic
- An adiabatic process is a process in which there
is no heat transfer with the surroundings. If the process is also
reversible, it is called isentropic. Typically, these processes are
fairly quick, in order not to give heat conduction enough time to do
its stuff, but not so excessively quick that they become
irreversible.
Adiabatic processes in quantum mechanics are defined quite
differently to keep students on their toes. See chapter
7.1.5. These processes are very slow, to give the
system all possible time to adjust to its surroundings. Of course,
quantum physicist were not aware that the same term had already been
used for a hundred years or so for relatively fast processes. They
assumed they had just invented a great new term!
- adjoint
- The adjoint
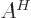 or
or 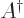 of an operator is
the one you get if you take it to the other side of an inner
product. (While keeping the value of the inner product the same
regardless of whatever two vectors or functions may be involved.)
Hermitian operators are
of an operator is
the one you get if you take it to the other side of an inner
product. (While keeping the value of the inner product the same
regardless of whatever two vectors or functions may be involved.)
Hermitian operators are self-adjoint;
they do not change if you take them to the other side of an inner
product. Skew-Hermitian
operators just change sign. Unitary operators
change into their inverse when taken to the other side of an inner
product. Unitary operators generalize rotations of vectors: an
inner product of vectors is the same whether you rotate the first
vector one way, or the second vector the opposite way. Unitary
operators preserve inner products (when applied to both vectors or
functions). Fourier transforms are unitary operators on account of
the Parseval equality that says that inner products are preserved.
- amplitude
- Everything in quantum mechanics is an amplitude.
However, most importantly, the
quantum amplitude
gives the coefficient of a state in a wave function. For example,
the usual quantum wave function gives the quantum amplitude that the
particle is at the given position.
- angle
- Consider two semi-infinite lines extending from a
common intersection point. Then the angle between these lines is
defined in the following way: draw a unit circle in the plane of the
lines and centered at their intersection point. The angle is then
the length of the circular arc that is in between the lines. More
precisely, this gives the angle in radians, rad. Sometimes an angle
is expressed in degrees, where
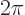 rad is taken to be
360
rad is taken to be
360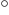 . However, using degrees is usually a very bad
idea in science.
. However, using degrees is usually a very bad
idea in science.
In three dimensions, you may be interested in the so-called
solid angle
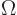 inside a conical surface. This
angle is defined in the following way: draw a sphere of unit radius
centered at the apex of the conical surface. Then the solid angle
is the area of the spherical surface that is inside the cone. Solid
angles are in steradians. The cone does not need to be a circular
one, (i.e. have a circular cross section), for this to apply. In
fact, the most common case is the solid angle corresponding to an
infinitesimal element
inside a conical surface. This
angle is defined in the following way: draw a sphere of unit radius
centered at the apex of the conical surface. Then the solid angle
is the area of the spherical surface that is inside the cone. Solid
angles are in steradians. The cone does not need to be a circular
one, (i.e. have a circular cross section), for this to apply. In
fact, the most common case is the solid angle corresponding to an
infinitesimal element 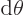

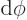 of spherical
coordinate system angles. In that case the surface of the unit
sphere inside the conical surface is is approximately rectangular,
with sides
of spherical
coordinate system angles. In that case the surface of the unit
sphere inside the conical surface is is approximately rectangular,
with sides 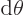 and
and 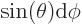 . That makes
the enclosed solid angle equal to
. That makes
the enclosed solid angle equal to 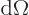

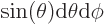 .
.
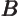
- May indicate:
- Repeatedly used to indicate a generic second operator or matrix.
- Einstein
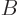 coefficient.
coefficient.
- Some constant.
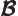
- May indicate:
- Magnetic field strength.
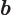
- May indicate:
- Repeatedly used to indicate the amplitude of the spin-down state
- Repeatedly used to indicate the amplitude of the second state
in a two-state system.
- End point of an integration interval.
- The second of a pair of particles.
- Some coefficient.
- Some constant.
- basis
- A basis is a minimal set of vectors or functions that
you can write all other vectors or functions in terms of. For
example, the unit vectors
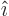 ,
, 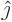 , and
, and 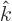 are a basis
for normal three-dimensional space. Every three-dimensional vector
can be written as a linear combination of the three.
are a basis
for normal three-dimensional space. Every three-dimensional vector
can be written as a linear combination of the three.
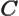
- May indicate:
- A third matrix or operator.
- A variety of different constants.
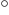 C
C - Degrees Centigrade. A commonly used
temperature scale that has the value
 273.15
273.15 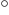 C
instead of zero when systems are in their ground state.
Recommendation: use degrees Kelvin (K) instead. However,
differences in temperature are the same in Centigrade as in Kelvin.
C
instead of zero when systems are in their ground state.
Recommendation: use degrees Kelvin (K) instead. However,
differences in temperature are the same in Centigrade as in Kelvin.
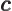
- May indicate:
- The speed of light, 299 792 458 m/s exactly (by definition of
the velocity unit).
- Speed of sound.
- Spring constant.
- A variety of different constants.
- Cauchy-Schwartz inequality
- The Cauchy-Schwartz inequality
describes a limitation on the magnitude of inner products. In
particular, it says that for any
 and
and 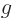 ,
,
In words, the magnitude of an inner product 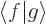 is at most the
magnitude (i.e. the length or norm) of
is at most the
magnitude (i.e. the length or norm) of  times the one of
times the one of
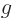 . For example, if
. For example, if  and
and 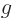 are real vectors, the inner
product is the dot product and you have
are real vectors, the inner
product is the dot product and you have 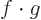

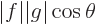 , where
, where 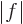 is the length of vector
is the length of vector  and
and  the one of
the one of 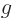 , and
, and 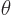 is the angle in between
the two vectors. Since a cosine is less than one in magnitude, the
Cauchy-Schwartz inequality is therefore true for vectors.
is the angle in between
the two vectors. Since a cosine is less than one in magnitude, the
Cauchy-Schwartz inequality is therefore true for vectors.
But it is true even if  and
and 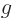 are functions. To prove it,
first recognize that
are functions. To prove it,
first recognize that 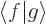 may in general be a complex number,
which according to (2.6) must take the form
may in general be a complex number,
which according to (2.6) must take the form
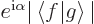 where
where 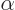 is some real number whose
value is not important, and that
is some real number whose
value is not important, and that 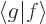 is its complex conjugate
is its complex conjugate
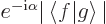 . Now, (yes, this is going to be
some convoluted reasoning), look at
. Now, (yes, this is going to be
some convoluted reasoning), look at
where 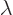 is any real number. The above dot product gives the
square magnitude of
is any real number. The above dot product gives the
square magnitude of 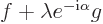 , so it can
never be negative. But if you multiply out, you get
, so it can
never be negative. But if you multiply out, you get
and if this quadratic form in 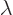 is never negative, its
discriminant must be less or equal to zero:
is never negative, its
discriminant must be less or equal to zero:
and taking square roots gives the Cauchy-Schwartz inequality.
- Classical
- Can mean any older theory. In this work, most of
the time it either means
nonquantum,
or
nonrelativistic.
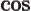
- The cosine function, a periodic function
oscillating between 1 and -1 as shown in
[41, pp. 40-]. See also
sin.
- curl
- The curl of a vector
 is defined as
is defined as
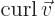

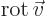



 .
.
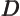
- May indicate:
- Difference in wave number values.
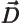
- Primitive (translation) vector of a
reciprocal lattice.
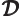
- Density of states.
- D
- Often used to indicate a state with two units of orbital
angular momentum.
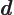
- May indicate:
- The distance between the protons of a hydrogen molecule.
- The distance between the atoms or lattice points in a crystal.
- A constant.
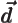
- Primitive (translation) vector of a
crystal lattice.
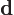
- Indicates a vanishingly small change or
interval of the following variable. For example,
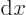 can be
thought of as a small segment of the
can be
thought of as a small segment of the  -axis.
-axis.
In three dimensions, 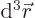

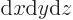 is an
infinitesimal volume element. The symbol
is an
infinitesimal volume element. The symbol 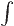 means that you sum
over all such infinitesimal volume elements.
means that you sum
over all such infinitesimal volume elements.
- derivative
- A derivative of a function is the ratio of a
vanishingly small change in a function divided by the vanishingly
small change in the independent variable that causes the change in
the function. The derivative of
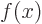 with respect to
with respect to  is
written as
is
written as 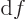 /
/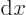 , or also simply as
, or also simply as 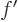 . Note that the
derivative of function
. Note that the
derivative of function 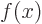 is again a function of
is again a function of  : a ratio
: a ratio
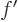 can be found at every point
can be found at every point  . The derivative of a function
. The derivative of a function
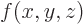 with respect to
with respect to  is written as
is written as
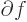 /
/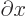 to indicate that there are other
variables,
to indicate that there are other
variables, 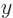 and
and  , that do not vary.
, that do not vary.
- determinant
- The determinant of a square matrix
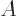 is a
single number indicated by
is a
single number indicated by 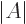 . If this number is nonzero,
. If this number is nonzero,
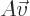 can be any vector
can be any vector 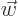 for the right choice of
for the right choice of
 . Conversely, if the determinant is zero,
. Conversely, if the determinant is zero, 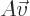 can only produce a very limited set of vectors, though if it can
produce a vector
can only produce a very limited set of vectors, though if it can
produce a vector 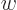 , it can do so for multiple vectors
, it can do so for multiple vectors
 .
.
There is a recursive algorithm that allows you to compute
determinants from increasingly bigger matrices in terms of
determinants of smaller matrices. For a 1  1 matrix
consisting of a single number, the determinant is simply that
number:
1 matrix
consisting of a single number, the determinant is simply that
number:
(This determinant should not be confused with the absolute value of
the number, which is written the same way. Since you normally do
not deal with 1  1 matrices, there is normally no
confusion.) For 2
1 matrices, there is normally no
confusion.) For 2  2 matrices, the determinant can be
written in terms of 1
2 matrices, the determinant can be
written in terms of 1  1 determinants:
1 determinants:
so the determinant is  in short.
For 3
in short.
For 3  3 matrices, you have
3 matrices, you have
and you already know how to work out those 2  2 determinants,
so you now know how to do 3
2 determinants,
so you now know how to do 3  3 determinants. Written out fully:
3 determinants. Written out fully:
For 4  4 determinants,
4 determinants,
Etcetera. Note the alternating sign pattern of the terms.
As you might infer from the above, computing a good size determinant
takes a large amount of work. Fortunately, it is possible to
simplify the matrix to put zeros in suitable locations, and that can
cut down the work of finding the determinant greatly. You are
allowed to use the following manipulations without seriously
affecting the computed determinant:
- You can
transpose
the matrix, i.e. change its columns into its rows.
- You can create zeros in a row by subtracting a suitable
multiple of another row.
- You can also swap rows, as long as you remember that each time
that you swap two rows, it will flip over the sign of the computed
determinant.
- You can also multiply an entire row by a constant, but that will
multiply the computed determinant by the same constant.
Applying these tricks in a systematic way, called “Gaussian
elimination” or “reduction to upper triangular
form”, you can eliminate all matrix coefficients 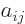 for
which
for
which  is less than
is less than  , and that makes evaluating the
determinant pretty much trivial.
, and that makes evaluating the
determinant pretty much trivial.
- div(ergence)
- The divergence of a vector
 is defined
as
is defined
as 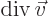

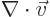 .
.
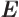
- May indicate:
- The total energy. Possible values are the eigenvalues of the
Hamiltonian.
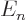

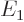 /
/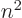

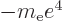 /
/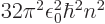

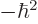 /
/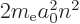

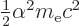 /
/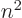 may indicate the nonrelativistic (Bohr) energy levels of the
hydrogen atom. The ground state energy
may indicate the nonrelativistic (Bohr) energy levels of the
hydrogen atom. The ground state energy 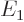 equals
-13.605 692 5 eV. This does not include relativistic and
proton motion corrections.
equals
-13.605 692 5 eV. This does not include relativistic and
proton motion corrections.
- Internal energy of a substance.
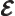
- May indicate:
- Electric field strength.
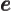
- May indicate:
- The basis for the natural logarithms. Equal to
2.718 281 828 459... This number produces the
exponential function
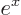 , or
, or
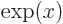 , or in words
, or in words 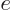 to the power
to the power 
,
whose derivative with respect to  is again
is again 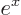 . If
. If 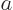 is a constant, then the derivative of
is a constant, then the derivative of 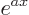 is
is 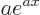 .
Also, if
.
Also, if 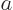 is an ordinary real number, then
is an ordinary real number, then 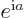 is a
complex number with magnitude 1.
is a
complex number with magnitude 1.
- The magnitude of the charge of an electron or proton, equal to
1.602 176 57 10
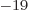 C.
C.
- Emissivity of electromagnetic radiation.
- Often used to indicate a unit vector.
- A superscript
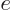 may indicate a single-electron quantity.
may indicate a single-electron quantity.
- Specific internal energy of a substance.
- e
- May indicate
- Subscript e may indicate an electron.
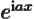
- Assuming that
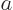 is an ordinary real
number, and
is an ordinary real
number, and  a real variable,
a real variable, 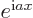 is a complex function
of magnitude one. The derivative of
is a complex function
of magnitude one. The derivative of 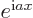 with respect to
with respect to
 is
is 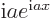
- eigenvector
- A concept from linear algebra. A vector
 is an eigenvector of a matrix
is an eigenvector of a matrix 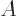 if
if  is nonzero
and
is nonzero
and 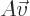

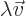 for some number
for some number 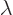 called the corresponding eigenvalue.
called the corresponding eigenvalue.
The basic quantum mechanics section of this book avoids linear
algebra completely, and the advanced part almost completely. The
few exceptions are almost all two-dimensional matrix eigenvalue
problems. In case you did not have any linear algebra, here is the
solution: the two-dimensional matrix eigenvalue problem
has eigenvalues that are the two roots of the quadratic equation
The corresponding eigenvectors are
On occasion you may have to swap 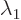 and
and 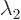 to use
these formulae. If
to use
these formulae. If 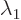 and
and 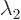 are equal, there
might not be two eigenvectors that are not multiples of each other;
then the matrix is called defective. However, Hermitian matrices
are never defective.
are equal, there
might not be two eigenvectors that are not multiples of each other;
then the matrix is called defective. However, Hermitian matrices
are never defective.
See also matrix” and “determinant.
- eV
- The electron volt, a commonly used unit of energy. Its
value is equal to 1.602 176 57 10
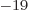 J.
J.
- exponential function
- A function of the form
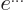 ,
also written as
,
also written as 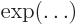 . See
. See function
and
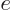 .
.
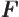
- May indicate:
- The force in Newtonian mechanics. Equal to the negative
gradient of the potential. Quantum mechanics is formulated in
terms of potentials, not forces.
- The anti-derivative of some function
 .
.
- Some function.
- Helmholtz free energy.
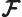
- Fock operator.
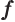
- May indicate:
- A generic function.
- A generic vector.
- A fraction.
- The resonance factor.
- Specific Helmholtz free energy.
- Frequency.
- function
- A mathematical object that associates values with
other values. A function
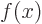 associates every value of
associates every value of  with
a value
with
a value  . For example, the function
. For example, the function 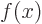

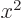 associates
associates 
 0 with
0 with 
 0,
0, 

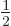 with
with


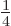 ,
, 
 1 with
1 with 
 1,
1, 
 2 with
2 with

 4,
4, 
 3 with
3 with 
 9, and more generally, any
arbitrary value of
9, and more generally, any
arbitrary value of  with the square of that value
with the square of that value 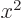 .
Similarly, function
.
Similarly, function 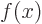

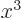 associates any arbitrary
associates any arbitrary  with its cube
with its cube 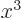 ,
, 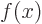

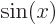 associates any arbitrary
associates any arbitrary
 with the sine of that value, etcetera.
with the sine of that value, etcetera.
One way of thinking of a function is as a procedure that allows you,
whenever given a number, to compute another number.
A wave function 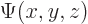 associates each spatial position
associates each spatial position
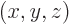 with a wave function value. Going beyond mathematics, its
square magnitude associates any spatial position with the relative
probability of finding the particle near there.
with a wave function value. Going beyond mathematics, its
square magnitude associates any spatial position with the relative
probability of finding the particle near there.
- functional
- A functional associates entire functions with
single numbers. For example, the expectation energy is
mathematically a functional: it associates any arbitrary wave
function with a number: the value of the expectation energy if
physics is described by that wave function.
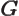
- May indicate:
- Gibbs free energy.
- Newton’s constant of gravitation, 6.673 8 10
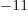 m
m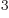 /kg s
/kg s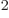 .
.
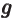
- May indicate:
- A second generic function or a second generic vector.
- The strength of gravity, by definition equal to 9.806 65
m/s
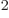 exactly under standard conditions on the surface of
the earth.
exactly under standard conditions on the surface of
the earth.
- The g-factor, a nondimensional constant that indicates the
gyromagnetic ratio relative to charge and mass. For the electron
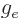

 2.002 319 304 361 5. For the proton
2.002 319 304 361 5. For the proton
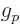
 5.585 694 71. For the neutron, based on the mass and
charge of the proton,
5.585 694 71. For the neutron, based on the mass and
charge of the proton, 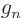

 3.826 085 5.
3.826 085 5.
- Specific Gibbs free energy/chemical potential.
- Gauss' Theorem
- This theorem, also called divergence theorem
or Gauss-Ostrogradsky theorem, says that for a continuously
differentiable vector
 ,
,
where the first integral is over the volume of an arbitrary region
and the second integral is over all the surface area of that region;
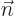 is at each point found as the unit vector that is normal
to the surface at that point.
is at each point found as the unit vector that is normal
to the surface at that point.
- grad(ient)
- The gradient of a scalar
 is defined as
is defined as
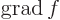

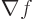 .
.
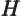
- May indicate:
- The Hamiltonian, or total energy, operator. Its eigenvalues
are indicated by
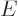 .
.
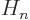 stands for the
stands for the 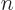 -th order Hermite polynomial.
-th order Hermite polynomial.
- Enthalpy.
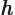
- May indicate:
- The original Planck constant
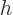

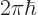 .
.
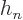 is a one-dimensional harmonic oscillator eigenfunction.
is a one-dimensional harmonic oscillator eigenfunction.
- Single-electron Hamiltonian.
- Specific enthalpy.
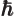
- The reduced Planck constant, equal to
1.054 571 73 10
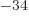 J s. A measure of the uncertainty of nature
in quantum mechanics. Multiply by
J s. A measure of the uncertainty of nature
in quantum mechanics. Multiply by 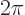 to get the original Planck
constant
to get the original Planck
constant 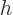 . For nuclear physics, a frequently helpful value is
. For nuclear physics, a frequently helpful value is
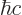
 197.326 972 MeV fm.
197.326 972 MeV fm.
- hypersphere
- A hypersphere is the generalization of the
normal three-dimensional sphere to
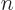 -dimensional space. A sphere of
radius
-dimensional space. A sphere of
radius 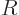 in three-dimensional space consists of all points
satisfying
in three-dimensional space consists of all points
satisfying
where 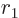 ,
, 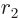 , and
, and 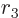 are Cartesian coordinates
with origin at the center of the sphere. Similarly a hypersphere in
are Cartesian coordinates
with origin at the center of the sphere. Similarly a hypersphere in
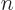 -dimensional space is defined as all points satisfying
-dimensional space is defined as all points satisfying
So a two-dimensional hypersphere
of radius 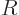 is really
just a circle of radius
is really
just a circle of radius 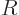 . A one-dimensional
. A one-dimensional
hypersphere
is really just the line segment 
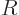
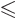

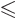

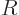 .
.
The volume” 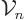 and surface “area
and surface “area
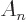 of an
of an 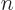 -dimensional hypersphere is given by
-dimensional hypersphere is given by
(This is readily derived recursively. For a sphere of unit radius,
note that the 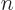 -dimensional
-dimensional volume
is an integration of
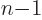 -dimensional volumes with respect to
-dimensional volumes with respect to 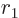 . Then renotate
. Then renotate 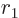 as
as 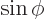 and look up the resulting integral in a table book.
The formula for the area follows because
and look up the resulting integral in a table book.
The formula for the area follows because 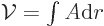 where
where
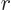 is the distance from the origin.) In three dimensions,
is the distance from the origin.) In three dimensions,
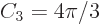 according to the above formula. That makes the
three-dimensional
according to the above formula. That makes the
three-dimensional volume
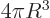
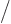 3 equal to the
actual volume of the sphere, and the three-dimensional
3 equal to the
actual volume of the sphere, and the three-dimensional
area
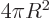 equal to the actual surface area.
On the other hand in two dimensions,
equal to the actual surface area.
On the other hand in two dimensions, 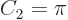 . That makes the
two-dimensional
. That makes the
two-dimensional volume
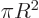 really the area
of the circle. Similarly the two-dimensional surface
really the area
of the circle. Similarly the two-dimensional surface
area
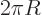 is really the perimeter of the
circle. In one dimensions
is really the perimeter of the
circle. In one dimensions 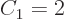 and the
and the volume
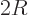 is really the length of the interval, and the
is really the length of the interval, and the
area
2 is really its number of end points.
Often the infinitesimal 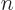 -dimensional
-dimensional volume
element 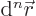 is needed. This is the infinitesimal integration
element for integration over all coordinates. It is:
is needed. This is the infinitesimal integration
element for integration over all coordinates. It is:
Specifically, in two dimensions:
while in three dimensions:
The expressions in parentheses are 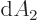 in polar coordinates,
respectively
in polar coordinates,
respectively 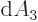 in spherical coordinates.
in spherical coordinates.
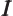
- May indicate:
- The number of electrons or particles.
- Electrical current.
- Unit matrix or operator, which does not do anything. See
matrix.
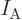 is Avogadro’s number, 6.022 141 3 10
is Avogadro’s number, 6.022 141 3 10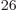 particles per kmol. (More standard symbols are
particles per kmol. (More standard symbols are 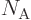 or
or
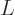 , but they are incompatible with the general notations in this
book.)
, but they are incompatible with the general notations in this
book.)
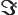
- The imaginary part of a complex number. If
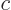

 with
with 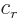 and
and 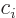 real numbers, then
real numbers, then
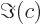

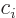 . Note that
. Note that 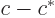

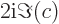 .
.
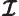
- May indicate:
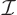 is radiation energy intensity.
is radiation energy intensity.
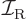 is moment of inertia.
is moment of inertia.
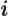
- May indicate:
- The number of a particle.
- A summation index.
- A generic index or counter.
Not to be confused with 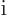 .
.
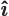
- The unit vector in the
 -direction.
-direction.
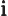
- The standard square root of minus one:
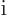

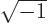 ,
, 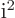

 1, 1/
1, 1/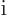

 ,
, 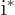

 .
.
- index notation
- A more concise and powerful way of writing
vector and matrix components by using a numerical index to indicate
the components. For Cartesian coordinates, you might number the
coordinates
 as 1,
as 1, 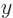 as 2, and
as 2, and  as 3. In that case, a sum
like
as 3. In that case, a sum
like 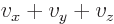 can be more concisely written as
can be more concisely written as 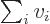 .
And a statement like
.
And a statement like 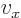
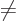 0,
0, 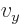
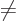 0,
0, 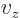
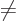 0 can
be more compactly written as
0 can
be more compactly written as 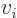
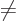 0. To really see how it
simplifies the notations, have a look at the matrix entry. (And that
one shows only 2 by 2 matrices. Just imagine 100 by 100 matrices.)
0. To really see how it
simplifies the notations, have a look at the matrix entry. (And that
one shows only 2 by 2 matrices. Just imagine 100 by 100 matrices.)
- iff
- Emphatic
if.
Should be read as
if and only if.
- integer
- Integer numbers are the whole numbers:
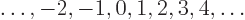 .
.
- inverse
- (Of matrices or operators.) If an operator
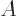 converts a vector or function
converts a vector or function  into a vector or function
into a vector or function
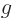 , then the inverse of the operator
, then the inverse of the operator 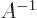 converts
converts 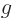 back into
back into  . For example, the operator 2 converts vectors
or functions into two times themselves, and its inverse operator
. For example, the operator 2 converts vectors
or functions into two times themselves, and its inverse operator
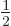 converts these back into the originals. Some operators do
not have inverses. For example, the operator 0 converts all vectors
or functions into zero. But given zero, there is no way to figure
out what function or vector it came from; the inverse operator does
not exist.
converts these back into the originals. Some operators do
not have inverses. For example, the operator 0 converts all vectors
or functions into zero. But given zero, there is no way to figure
out what function or vector it came from; the inverse operator does
not exist.
- irrotational
- A vector
 is irrotational if its curl
is irrotational if its curl


 is zero.
is zero.
- iso
- Means
equal” or “constant.
- Isenthalpic: constant enthalpy.
- Isentropic: constant entropy. This is a process that is both
adiabatic and reversible.
- Isobaric: constant pressure.
- Isochoric: constant (specific) volume.
- Isospin: you don’t want to know.
- Isothermal: constant temperature.
- isolated
- An isolated system is one that does not interact
with its surroundings in any way. No heat is transfered with the
surroundings, no work is done on or by the surroundings.
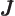
- May indicate:
- Total angular momentum.
- Number of nuclei in a quantum computation of electronic structure.
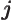
- May indicate:
- The azimuthal quantum number of total angular momentum,
including both orbital and spin contributions.
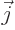 is electric current density.
is electric current density.
- The number of a nucleus in a quantum computation.
- A summation index.
- A generic index or counter.
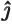
- The unit vector in the
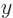 -direction.
-direction.
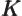
- May indicate:
- An exchange integral in Hartree-Fock.
- Maximum wave number value.
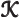
- Thomson (Kelvin) coefficient.
- K
- May indicate:
- The atomic states or orbitals with theoretical Bohr energy
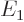
- Degrees Kelvin.
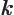
- May indicate:
- A wave number. A wave number is a measure for how fast a
periodic function oscillates with variations in spatial position.
In quantum mechanics,
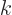 is normally defined as
is normally defined as
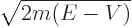 /
/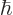 . The vector
. The vector 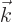 is not to be
confused with the unit vector in the
is not to be
confused with the unit vector in the  -direction
-direction 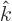 .
.
- A generic summation index.
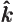
- The unit vector in the
 -direction.
-direction.
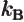
- Boltzmann constant. Equal to
1.380 649 10
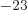 J/K. Relates absolute temperature to a typical
unit of heat motion energy.
J/K. Relates absolute temperature to a typical
unit of heat motion energy.
- kmol
- A kilo mole refers to 6.022 141 3 10
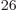 atoms or
molecules. The weight of this many particles is about the number of
protons and neutrons in the atom nucleus/molecule nuclei. So a kmol
of hydrogen atoms has a mass of about 1 kg, and a kmol of hydrogen
molecules about 2 kg. A kmol of helium atoms has a mass of about 4
kg, since helium has two protons and two neutrons in its nucleus.
These numbers are not very accurate, not just because the electron
masses are ignored, and the free neutron and proton masses are
somewhat different, but also because of relativity effects that
cause actual nuclear masses to deviate from the sum of the free
proton and neutron masses.
atoms or
molecules. The weight of this many particles is about the number of
protons and neutrons in the atom nucleus/molecule nuclei. So a kmol
of hydrogen atoms has a mass of about 1 kg, and a kmol of hydrogen
molecules about 2 kg. A kmol of helium atoms has a mass of about 4
kg, since helium has two protons and two neutrons in its nucleus.
These numbers are not very accurate, not just because the electron
masses are ignored, and the free neutron and proton masses are
somewhat different, but also because of relativity effects that
cause actual nuclear masses to deviate from the sum of the free
proton and neutron masses.
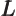
- May indicate:
- Angular momentum.
- Orbital angular momentum.
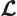
- Lagrangian.
- L
- The atomic states or orbitals with theoretical Bohr energy
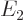
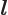
- May indicate:
- The azimuthal quantum number of angular momentum.
- The azimuthal quantum number of orbital angular momentum.
Here
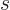 is used for spin, and
is used for spin, and  for combined angular
momentum.)
for combined angular
momentum.)
- A generic summation index.
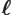
- May indicate:
- The typical length in the harmonic oscillator problem.
- The dimensions of a solid block (with subscripts).
- A length.
- Multipole level in transitions.
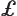
- Lagrangian density. This is best understood
in the UK.
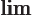
- Indicates the final result of an approaching
process.
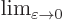 indicates for practical purposes
the value of the following expression when
indicates for practical purposes
the value of the following expression when 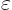 is
extremely small.
is
extremely small.
- linear combination
- A very generic concept indicating sums of
objects times coefficients. For example, a position vector
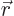 in
basic physics is the linear combination
in
basic physics is the linear combination 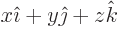 with
the objects the unit vectors
with
the objects the unit vectors 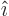 ,
, 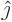 , and
, and 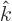 and the
coefficients the position coordinates
and the
coefficients the position coordinates  ,
, 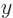 , and
, and  . A linear
combination of a set of functions
. A linear
combination of a set of functions
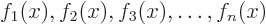 would be the function
would be the function
where 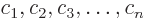 are constants, i.e. independent of
are constants, i.e. independent of
 .
.
- linear dependence
- A set of vectors or functions is linearly
dependent if at least one of the set can be expressed in terms of
the others. Consider the example of a set of functions
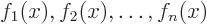 . This set is linearly dependent
if
. This set is linearly dependent
if
where at least one of the constants 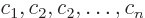 is
nonzero. To see why, suppose that say
is
nonzero. To see why, suppose that say 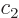 is nonzero. Then you
can divide by
is nonzero. Then you
can divide by 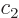 and rearrange to get
and rearrange to get
That expresses 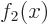 in terms of the other functions.
in terms of the other functions.
- linear independence
- A set of vectors or functions is
linearly independent if none of the set can be expressed in terms of
the others. Consider the example of a set of functions
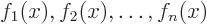 . This set is linearly
independent if
. This set is linearly
independent if
only if every one of the constants 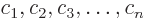 is zero.
To see why, assume that say
is zero.
To see why, assume that say 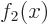 could be expressed in terms
of the others,
could be expressed in terms
of the others,
Then taking 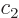
 1,
1, 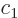

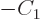 ,
, 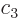

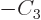 , ...
, ...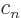

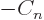 , the condition above
would be violated. So
, the condition above
would be violated. So 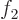 cannot be expressed in terms of the
others.
cannot be expressed in terms of the
others.
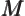
- May indicate:
- Molecular mass. See
molecular mass.
- Figure of merit.
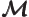
- Mirror operator.
- M
- The atomic states or orbitals with theoretical Bohr energy
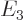
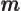
- May indicate:
- Mass.
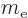 : electron mass. Equal to
9.109 382 9 10
: electron mass. Equal to
9.109 382 9 10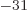 kg. The rest mass energy is
0.510 998 93 MeV.
kg. The rest mass energy is
0.510 998 93 MeV.
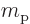 : proton mass. Equal to
1.672 621 78 10
: proton mass. Equal to
1.672 621 78 10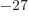 kg. The rest mass energy is
938.272 013 MeV.
kg. The rest mass energy is
938.272 013 MeV.
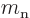 : neutron mass. Equal to
1.674 927 10
: neutron mass. Equal to
1.674 927 10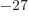 kg. The rest mass energy is 939.565 561
MeV.
kg. The rest mass energy is 939.565 561
MeV.
- Alpha particle: 6.644 656 8 10
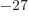 kg or 3 727.379 24 MeV.
kg or 3 727.379 24 MeV.
Deuteron: 3.343 583 5 10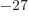 kg or 1 875.612 86 MeV.
kg or 1 875.612 86 MeV.
Helion: 5.006 412 3 10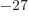 kg or 2 808.391 482 MeV.
kg or 2 808.391 482 MeV.
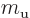
 1.660 538 92 10
1.660 538 92 10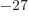 kg is the atomic
mass constant.
kg is the atomic
mass constant.
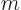 : generic particle mass.
: generic particle mass.
- The magnetic quantum number of angular momentum. The type odf
angular momentum may be indicated by a subscript
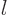 for orbital,
for orbital,
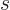 for spin, or
for spin, or  for net (orbital plus spin).
for net (orbital plus spin).
- Number of a single-electron wave function.
- Number of rows in a matrix.
- A generic summation index or generic integer.
- matrix
- A table of numbers.
As a simple example, a two-dimensional (or 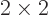 ) matrix
) matrix 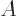 is
a table of four numbers called
is
a table of four numbers called 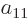 ,
, 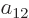 ,
, 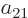 , and
, and
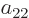 :
:
unlike a two-dimensional vector  , which would consist of
only two numbers
, which would consist of
only two numbers 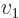 and
and 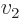 arranged in a column:
arranged in a column:
(Such a vector can be seen as a rectangular matrix
of size 2  1, but let’s not get into that.) (Note that
in quantum mechanics, if a vector is written as a column, considered
the normal case, it is called a
1, but let’s not get into that.) (Note that
in quantum mechanics, if a vector is written as a column, considered
the normal case, it is called a
ket
vector. If the complex
conjugates of its numbers are written as a row, it is called a
bra
vector.)
In index notation,
a
matrix 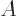 is a set of numbers, or
is a set of numbers, or coefficients,
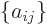 indexed by two indices. The first index
indexed by two indices. The first index  is the row
number at which the coefficient
is the row
number at which the coefficient 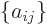 is found in matrix
is found in matrix 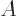 ,
and the second index
,
and the second index  is the column number. In index notation, a
matrix turns a vector
is the column number. In index notation, a
matrix turns a vector  into another vector
into another vector
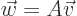 according to the recipe
according to the recipe
where 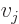 stands for “the
stands for “the  -th component of vector
-th component of vector
 ,” and
,” and 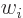 for “the
for “the  -th component of
vector
-th component of
vector 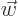 .”
.”
As an example, the product of 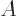 and
and  above is by
definition
above is by
definition
which is just another two-dimensional ket vector.
Note that in matrix multiplications, like in the example above, in
geometric terms you take dot products between the rows of the first
factor and the columns of the second factor.
To multiply two matrices together, just think of the columns of the
second matrix as separate vectors. For example, to multiply
two 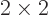 matrices
matrices 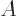 and
and 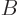 together:
together:
which is another two-dimensional matrix.
(Note that you cannot normally swap the order of matric
multiplication. The matrix 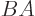 is different from matrix
is different from matrix 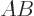 . In
the special case that
. In
the special case that 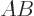 and
and 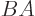 are the same and
are the same and 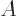 and
and 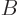 have complete sets of eigenvectors, then they have a common complete
set of eigenvectors, {D.18}.)
have complete sets of eigenvectors, then they have a common complete
set of eigenvectors, {D.18}.)
In index notation, if 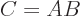 , then each coefficient
, then each coefficient 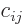 of
matrix
of
matrix 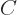 is given in terms of the coefficients of
is given in terms of the coefficients of 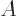 and
and 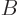 as
as
Note that the index 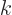 that you sum over is the second of
that you sum over is the second of 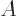 but
the first of
but
the first of 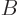 . In short, you sum over “neighboring
indices.” Since you sum over all
. In short, you sum over “neighboring
indices.” Since you sum over all 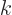 , the result does not
depend on
, the result does not
depend on 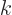 .
.
The zero matrix, usually called 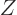 , is like the number zero; it
does not change a matrix it is added to. And it turns whatever it
is multiplied with into zero. A zero matrix has every coefficient
zero. For example, in two dimensions:
, is like the number zero; it
does not change a matrix it is added to. And it turns whatever it
is multiplied with into zero. A zero matrix has every coefficient
zero. For example, in two dimensions:
A unit, or identity, matrix, usually called 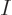 , is the equivalent
of the number one for matrices; it does not change the vector or
matrix it is multiplied with. A unit matrix is one on its
, is the equivalent
of the number one for matrices; it does not change the vector or
matrix it is multiplied with. A unit matrix is one on its
main diagonal
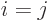 and zero elsewhere. The 2 by 2
unit matrix is:
and zero elsewhere. The 2 by 2
unit matrix is:
More generally the coefficients, 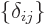 , of a unit matrix
are one if
, of a unit matrix
are one if 

 and zero otherwise.
and zero otherwise.
The transpose
of a
matrix 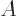 ,
, 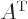 , is what you get if you swap the two
indices. Graphically, it turns its rows into its columns and vice
versa. The
, is what you get if you swap the two
indices. Graphically, it turns its rows into its columns and vice
versa. The adjoint
or Hermitian adjoint
matrix 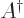 is what you
get if you both swap the two indices in a matrix
is what you
get if you both swap the two indices in a matrix 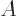 and then take
the complex conjugate of every coefficient. If you want to take a
matrix to the other side of an inner product, you will need to
change it to its Hermitian adjoint.
and then take
the complex conjugate of every coefficient. If you want to take a
matrix to the other side of an inner product, you will need to
change it to its Hermitian adjoint. Hermitian matrices
are equal to their Hermitian adjoint, so this does nothing for them.
The inverse of a matrix 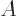 ,
, 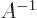 is a matrix so that
is a matrix so that 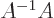 equals the identity matrix
equals the identity matrix 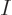 . That is much like the inverse of a
simple number times that number gives one. And, just like the
number zero has no inverse, a matrix with zero determinant has no
inverse. Otherwise, you can swap the order;
. That is much like the inverse of a
simple number times that number gives one. And, just like the
number zero has no inverse, a matrix with zero determinant has no
inverse. Otherwise, you can swap the order; 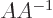 equals the
unit matrix too. (For numbers this is trivial, for matrices you
need to look a bit closer to understand why it is true.)
equals the
unit matrix too. (For numbers this is trivial, for matrices you
need to look a bit closer to understand why it is true.)
See also determinant
and
eigenvector.
- metric prefixes
- In the metric system, the prefixes Y, Z, E,
P, T, G, M, and k stand for 10
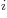 with
with 
 24, 21, 18, 15,
12, 9, 6, and 3, respectively. Similarly, d, c, m,
24, 21, 18, 15,
12, 9, 6, and 3, respectively. Similarly, d, c, m, 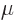 , n, p, f,
a, z, y stand for 10
, n, p, f,
a, z, y stand for 10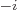 with
with 
 1, 2, 3, 6, 9, 12, 15,
18, 21, and 24 respectively. For example, 1 ns is 10
1, 2, 3, 6, 9, 12, 15,
18, 21, and 24 respectively. For example, 1 ns is 10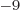 seconds. English letter u is often used as instead of greek
seconds. English letter u is often used as instead of greek 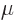 .
Names corresponding to the mentioned prefixes Y-k are yotta, zetta,
exa, peta, tera, giga, mega, kilo, and corresponding to d-y are
deci, centi, milli, micro, nano, pico, femto, atto, zepto, and
yocto.
.
Names corresponding to the mentioned prefixes Y-k are yotta, zetta,
exa, peta, tera, giga, mega, kilo, and corresponding to d-y are
deci, centi, milli, micro, nano, pico, femto, atto, zepto, and
yocto.
- molecular mass
- Typical thermodynamics books for engineers
tabulate values of the
molecular mass,
as a
nondimensional number. The bottom line first: these numbers should
have been called the molar mass
of the
substance, for the naturally occurring isotope ratio on earth. And
they should have been given units of kg/kmol. That is how you use
these numbers in actual computations. So just ignore the fact that
what these books really tabulate is officially called the
relative molecular mass
for the natural
isotope ratio.
Don’t blame these textbooks too much for making a mess of
things. Physicists have historically bandied about a zillion
different names for what is essentially a single number. Like
molecular mass,
“relative molecular
mass,” molecular weight,
“atomic
mass,” relative atomic mass,
“atomic
weight,” molar mass,
“relative molar
mass,” etcetera are basically all the same thing.
All of these have values that equal the mass of a molecule relative
to a reference value for a single nucleon. So these value are about
equal to the number of nucleons (protons and neutrons) in the nuclei
of a single molecule. (For an isotope ratio, that becomes the
average number of nucleons. Do note that nuclei are sufficiently
relativistic that a proton or neutron can be noticeably heavier in
one nucleus than another, and that neutrons are a bit heavier than
protons even in isolation.) The official reference nucleon weight
is defined based on the most common carbon isotope carbon-12. Since
carbon-12 has 6 protons plus 6 neutrons, the reference nucleon
weight is taken to be one twelfth of the carbon-12 atomic weight.
That is called the unified atomic mass unit (u) or Dalton (Da). The
atomic mass unit (amu) is an older virtually identical unit, but
physicists and chemists could never quite agree on what its value
was. No kidding.
If you want to be politically correct, the deal is as follows.
Molecular mass
is just what the term says, the mass
of a molecule, in mass units. (I found zero evidence in either the
IUPAC Gold Book or NIST SP811 for the claim of Wikipedia that it
must always be expressed in u.) Molar mass
is just
what the words says, the mass of a mole. Official SI units are
kg/mol, but you will find it in g/mol, equivalent to kg/kmol. (You
cannot expect enough brains from international committees to realize
that if you define the kg and not the g as unit of mass, then it
would be a smart idea to also define kmol instead of mol as unit of
particle count.) Simply ignore relative atomic and molecular
masses, you do not care about them. (I found zero evidence in
either the IUPAC Gold Book or NIST SP811 for the claims of Wikipedia
that the molecular mass cannot be an average over isotopes or that
the molar mass must be for a natural isotope ratio. In fact, NIST
uses molar mass of carbon-12
and specifically
includes the possibility of an average in the relative molecular
mass.)
See also the atomic mass constant
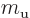 .
.
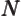
- May indicate:
- Number of states.
- Number of single-particle states.
- Number of neutrons in a nucleus.
- N
- May indicate
- The atomic states or orbitals with theoretical Bohr energy
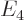 .
.
- Subscript N indicates a nucleus.
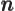
- May indicate:
- The principal quantum number for hydrogen atom energy
eigenfunctions.
- A quantum number for harmonic oscillator energy
eigenfunctions.
- Number of a single-electron or single-particle wave function.
- Generic summation index over energy eigenfunctions.
- Generic summation index over other eigenfunctions.
- Integer factor in Fourier wave numbers.
- Probability density.
- Number of columns in a matrix.
- A generic summation index or generic integer.
- A natural number.
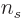 is the number of spin states.
is the number of spin states.
and maybe some other stuff.
- n
- May indicate
- A subscript n may indicate a neutron.
- natural
- Natural numbers are the numbers:
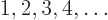 .
.
- normal
- A normal operator or matrix is one that has
orthonormal eigenfunctions or eigenvectors. Since eigenvectors are
not orthonormal in general, a normal operator or matrix is abnormal!
Another example of a highly confusing term. Such a matrix should
have been called orthodiagonalizable or something of the kind. To
be fair, the author is not aware of any physicists being involved in
this particular term; it may be the mathematicians that are to blame
here.
For an operator or matrix 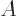 to be
to be normal,
it must
commute with its Hermitian adjoint, ![$[A,A^\dagger]$](img8212.gif)
 0. Hermitian
matrices are normal since they are equal to their Hermitian adjoint.
Skew-Hermitian matrices are normal since they are equal to the
negative of their Hermitian adjoint. Unitary matrices are normal
because they are the inverse of their Hermitian adjoint.
0. Hermitian
matrices are normal since they are equal to their Hermitian adjoint.
Skew-Hermitian matrices are normal since they are equal to the
negative of their Hermitian adjoint. Unitary matrices are normal
because they are the inverse of their Hermitian adjoint.
- O
- May indicate the origin of the coordinate system.
- opposite
- The opposite of a number
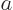 is
is 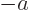 . In other
words, it is the additive inverse.
. In other
words, it is the additive inverse.
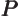
- May indicate:
- The linear momentum eigenfunction.
- A power series solution.
- Probability.
- Pressure.
- Hermitian part of an annihilation operator.
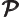
- Particle exchange operator. Exchanges the
positions and spins of two identical particles.
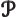
- Peltier coefficient.
- P
- Often used to indicate a state with one unit of orbital
angular momentum.
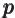
- May indicate:
- Linear momentum.
- Linear momentum in the
 -direction.
-direction.
- Integration variable with units of linear momentum.
- p
- May indicate
- An energy state with orbital azimuthal quantum number
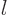
 1.
1.
- A superscript p may indicate a single-particle quantity.
- A subscript p may indicate a periodic function.
- A subscript p may indicate a proton.
- perpendicular bisector
- For two given points
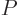 and
and 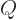 , the
perpendicular bisector consists of all points
, the
perpendicular bisector consists of all points 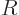 that are equally
far from
that are equally
far from 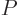 as they are from
as they are from 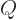 . In two dimensions, the
perpendicular bisector is the line that passes through the point
exactly half way in between
. In two dimensions, the
perpendicular bisector is the line that passes through the point
exactly half way in between 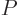 and
and 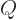 , and that is orthogonal to
the line connecting
, and that is orthogonal to
the line connecting 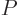 and
and 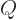 . In three dimensions, the
perpendicular bisector is the plane that passes through the point
exactly half way in between
. In three dimensions, the
perpendicular bisector is the plane that passes through the point
exactly half way in between 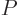 and
and 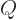 , and that is orthogonal to
the line connecting
, and that is orthogonal to
the line connecting 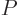 and
and 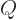 . In vector notation, the
perpendicular bisector of points
. In vector notation, the
perpendicular bisector of points 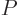 and
and 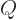 is all points
is all points 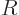 whose
radius vector
whose
radius vector 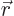 satisfies the equation:
satisfies the equation:
(Note that the halfway point 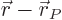

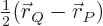 is included in this formula, as is the half
way point plus any vector that is normal to
is included in this formula, as is the half
way point plus any vector that is normal to 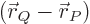 .)
.)
- phase angle
- Any complex number can be written in
polar form
as 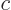

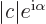 where
both the magnitude
where
both the magnitude  and the phase angle
and the phase angle 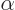 are real
numbers. Note that when the phase angle varies from zero to
are real
numbers. Note that when the phase angle varies from zero to 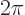 ,
the complex number
,
the complex number 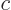 varies from positive real to positive
imaginary to negative real to negative imaginary and back to
positive real. When the complex number is plotted in the complex
plane, the phase angle is the direction of the number relative to
the origin. The phase angle
varies from positive real to positive
imaginary to negative real to negative imaginary and back to
positive real. When the complex number is plotted in the complex
plane, the phase angle is the direction of the number relative to
the origin. The phase angle 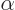 is often called the argument,
but so is about everything else in mathematics, so that is not very
helpful.
is often called the argument,
but so is about everything else in mathematics, so that is not very
helpful.
In complex time-dependent waves of the form
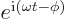 , and its real equivalent
, and its real equivalent
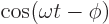 , the phase angle
, the phase angle 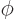 gives the
angular argument of the wave at time zero.
gives the
angular argument of the wave at time zero.
- photon
- Unit of electromagnetic radiation (which includes
light, x-rays, microwaves, etcetera). A photon has a energy
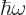 , where
, where 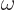 is its angular frequency, and a
wave length
is its angular frequency, and a
wave length 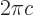 /
/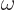 where
where 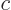 is the speed of light.
is the speed of light.
- potential
- In order to optimize confusion, pretty much
everything in physics that is scalar is called potential. Potential
energy is routinely concisely referred to as potential. It is the
energy that a particle can pick up from a force field by changing
its position. It is in Joule. But an electric potential is taken to
be per unit charge, which gives it units of volts. Then there are
thermodynamic potentials like the chemical potential.
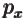
- Linear momentum in the
 -direction. (In the
one-dimensional cases at the end of the unsteady evolution chapter,
the
-direction. (In the
one-dimensional cases at the end of the unsteady evolution chapter,
the  subscript is omitted.) Components in the
subscript is omitted.) Components in the 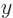 - and
- and
 -directions are
-directions are 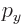 and
and 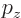 . Classical Newtonian
physics has
. Classical Newtonian
physics has 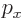

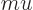 where
where 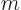 is the mass and
is the mass and 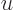 the
velocity in the
the
velocity in the  -direction. In quantum mechanics, the possible
values of
-direction. In quantum mechanics, the possible
values of 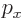 are the eigenvalues of the operator
are the eigenvalues of the operator 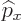 which
equals
which
equals 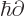 /
/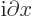 . (But which becomes
canonical momentum in a magnetic field.)
. (But which becomes
canonical momentum in a magnetic field.)
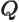
- May indicate
- Number of energy eigenfunctions of a system of particles.
- Anti-Hermitian part of an annihilation operator divided by
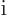 .
.
- Heat flow or heat.
- Charge.
- Electric quadrupole moment.
- Energy release.
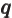
- May indicate:
- Charge.
- Heat flux density.
- The number of an energy eigenfunction of a system of
particles.
- Generic index.
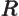
- May indicate:
- Ideal gas constant.
- Transition rate.
- Nuclear radius.
- Reflection coefficient.
- Some radius or typical radius (like in the Yukawa potential).
- Some function of
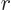 to be determined.
to be determined.
- Some function of
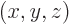 to be determined.
to be determined.
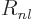 is a hydrogen radial wave function.
is a hydrogen radial wave function.
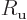
 8.314 462 kJ/kmol K is the universal gas constant.
It is the equivalent of Boltzmann's constant, but for a kmol
instead of a single atom or molecule.
8.314 462 kJ/kmol K is the universal gas constant.
It is the equivalent of Boltzmann's constant, but for a kmol
instead of a single atom or molecule.
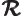
- Rotation operator.
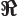
- The real part of a complex number. If
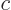

 with
with 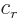 and
and 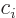 real numbers, then
real numbers, then

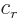 . Note that
. Note that 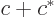

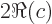 .
.
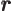
- May indicate:
- The radial distance from the chosen origin of the coordinate
system.
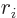 typically indicates the
typically indicates the  -th Cartesian component of
the radius vector
-th Cartesian component of
the radius vector 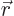 .
.
- Some ratio.
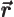
- The position vector. In Cartesian coordinates
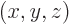 or
or 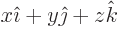 . In spherical coordinates
. In spherical coordinates
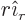 . Its three Cartesian components may be indicated by
. Its three Cartesian components may be indicated by
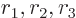 or by
or by 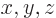 or by
or by 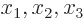 .
.
- reciprocal
- The reciprocal of a number
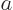 is 1/
is 1/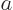 .
In other words, it is the multiplicative inverse.
.
In other words, it is the multiplicative inverse.
- relativity
- The special theory of relativity accounts for the
experimental observation that the speed of light
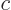 is the same in
all local coordinate systems. It necessarily drops the basic
concepts of absolute time and length that were corner stones in
Newtonian physics.
is the same in
all local coordinate systems. It necessarily drops the basic
concepts of absolute time and length that were corner stones in
Newtonian physics.
Albert Einstein should be credited with the boldness to squarely
face up to the unavoidable where others wavered. However, he should
also be credited for the boldness of swiping the basic ideas from
Lorentz and Poincaré without giving them proper, or any, credit.
The evidence is very strong he was aware of both works, and his
various arguments are almost carbon copies of those of Poincaré,
but in his paper it looks like it all came from Einstein, with the
existence of the earlier works not mentioned. (Note that the
general theory of relativity, which is of no interest to this book,
is almost surely properly credited to Einstein. But he was a lot
less hungry then.)
Relativity implies that a length seen by an observer moving at a
speed 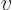 is shorter than the one seen by a stationary observer by a
factor
is shorter than the one seen by a stationary observer by a
factor 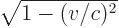 assuming the length is in the direction of
motion. This is called Lorentz-Fitzgerald contraction. It makes
galactic travel somewhat more conceivable because the size of the
galaxy will contract for an astronaut in a rocket ship moving close
to the speed of light. Relativity also implies that the time that
an event takes seems to be slower by a factor
assuming the length is in the direction of
motion. This is called Lorentz-Fitzgerald contraction. It makes
galactic travel somewhat more conceivable because the size of the
galaxy will contract for an astronaut in a rocket ship moving close
to the speed of light. Relativity also implies that the time that
an event takes seems to be slower by a factor  if the event is seen by an observer in motion compared to the
location where the event occurs. That is called time dilation.
Some high-energy particles generated in space move so fast that they
reach the surface of the earth though this takes much more time than
the particles would last at rest in a laboratory. The decay time
increases because of the motion of the particles. (Of course, as
far as the particles themselves see it, the distance to travel is a
lot shorter than it seems to be to earth. For them, it is a matter
of length contraction.)
if the event is seen by an observer in motion compared to the
location where the event occurs. That is called time dilation.
Some high-energy particles generated in space move so fast that they
reach the surface of the earth though this takes much more time than
the particles would last at rest in a laboratory. The decay time
increases because of the motion of the particles. (Of course, as
far as the particles themselves see it, the distance to travel is a
lot shorter than it seems to be to earth. For them, it is a matter
of length contraction.)
The following formulae give the relativistic mass, momentum, and
kinetic energy of a particle in motion:
where 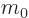 is the rest mass of the particle, i.e. the mass as
measured by an observer to whom the particle seems at rest. The
formula for kinetic energy reflects the fact that even if a particle
is at rest, it still has an amount of
is the rest mass of the particle, i.e. the mass as
measured by an observer to whom the particle seems at rest. The
formula for kinetic energy reflects the fact that even if a particle
is at rest, it still has an amount of build-in
energy equal to 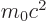 left. The total energy of a particle in
empty space, being kinetic and rest mass energy, is given by
left. The total energy of a particle in
empty space, being kinetic and rest mass energy, is given by
as can be verified by substituting in the expression for the
momentum, in terms of the rest mass, and then taking both terms
inside the square root under a common denominator. For small linear
momentum 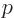 , this can be approximated as
, this can be approximated as
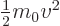 .
.
Relativity seemed quite a dramatic departure of Newtonian physics
when it developed. Then quantum mechanics started to emerge...
- rot
- The rot of a vector
 is defined as
is defined as
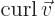

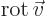



 .
.
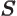
- May indicate:
- Number of states per unit volume.
- Number of states at a given energy level.
- Spin angular momentum (as an alternative to using
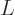 or
or 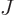 for generic angular momentum.)
for generic angular momentum.)
- Entropy.
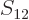 is a factor in the so-called tensor potential of nucleons.
is a factor in the so-called tensor potential of nucleons.
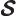
- The action integral of Lagrangian mechanics,
{A.1}
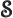
- Seebeck coefficient.
- S
- Often used to indicate a state of zero orbital angular
momentum.
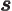
- May indicate:
- Spin value of a particle. Equals
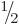 for electrons,
protons, and neutrons, is also half an odd natural number for
other fermions, and is a nonnegative integer for bosons. It is
the azimuthal quantum number
for electrons,
protons, and neutrons, is also half an odd natural number for
other fermions, and is a nonnegative integer for bosons. It is
the azimuthal quantum number 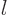 due to spin.
due to spin.
- Specific entropy.
- As an index, shelf number.
- s
- May indicate:
- An energy state with orbital azimuthal quantum number
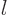
 0. Such a state is spherically symmetric.
0. Such a state is spherically symmetric.
- scalar
- A quantity that is not a vector, a quantity that is
just a single number.
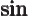
- The sine function, a periodic function
oscillating between 1 and -1 as shown in
[41, pp. 40-]. Good to remember:
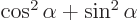
 1 and
1 and 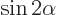

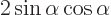 and
and 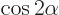

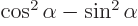 .
.
- solenoidal
- A vector
 is solenoidal if its
divergence
is solenoidal if its
divergence 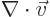 is zero.
is zero.
- spectrum
- In this book, a spectrum normally means a plot of
energy levels along the vertical axis. Often, the horizontal
coordinate is used to indicate a second variable, such as the
density of states or the particle velocity.
For light (photons), a spectrum can be obtained experimentally by
sending the light through a prism. This separates the colors in the
light, and each color means a particular energy of the photons.
The word spectrum is also often used in a more general mathematical
sense, but not in this book as far as I can remember.
- spherical coordinates
- The spherical coordinates
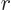 ,
,
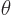 , and
, and 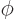 of an arbitrary point P are defined as
of an arbitrary point P are defined as
Figure N.3:
Spherical coordinates of an arbitrary point P.
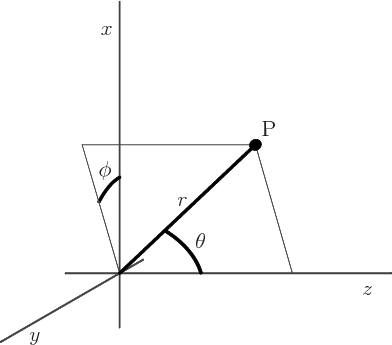 |
In Cartesian coordinates, the unit vectors in the  ,
,
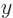 , and
, and  directions are called
directions are called 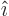 ,
,
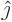 , and
, and 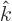 . Similarly, in spherical
coordinates, the unit vectors in the
. Similarly, in spherical
coordinates, the unit vectors in the 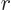 ,
, 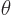 , and
, and
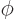 directions are called
directions are called 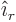 ,
, 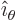 ,
and
,
and 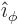 . Here, say, the
. Here, say, the 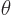 direction is
defined as the direction of the change in position if you increase
direction is
defined as the direction of the change in position if you increase
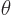 by an infinitesimally small amount while keeping
by an infinitesimally small amount while keeping 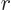 and
and
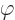 the same. Note therefore in particular that the direction
of
the same. Note therefore in particular that the direction
of 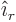 is the same as that of
is the same as that of 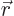 ; radially outward.
; radially outward.
An arbitrary vector  can be decomposed in components
can be decomposed in components
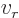 ,
, 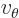 , and
, and 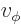 along these unit
vectors. In particular
along these unit
vectors. In particular
Recall from calculus that in spherical coordinates, a volume
integral of an arbitrary function  takes the form
takes the form
In other words, the volume element in spherical coordinates is
Often it is convenient of think of volume integrations as a two-step
process: first perform an integration over the angular coordinates
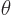 and
and 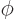 . Physically, that integrates over
spherical surfaces. Then perform an integration over
. Physically, that integrates over
spherical surfaces. Then perform an integration over 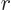 to
integrate all the spherical surfaces together. The combined
infinitesimal angular integration element
to
integrate all the spherical surfaces together. The combined
infinitesimal angular integration element
is called the infinitesimal solid angle
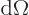 . In two-dimensional polar coordinates
. In two-dimensional polar coordinates 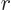 and
and
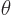 , the equivalent would be the infinitesimal polar
angle
, the equivalent would be the infinitesimal polar
angle 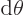 . Recall that
. Recall that 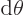 , (in proper
radians of course), equals the arclength of an infinitesimal part of
the circle of integration divided by the circle radius. Similarly
, (in proper
radians of course), equals the arclength of an infinitesimal part of
the circle of integration divided by the circle radius. Similarly
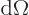 is the surface of an infinitesimal part of the sphere of
integration divided by the square sphere radius.
is the surface of an infinitesimal part of the sphere of
integration divided by the square sphere radius.
See the 
entry for the gradient operator
and Laplacian in spherical coordinates.
- Stokes' Theorem
- This theorem, first derived by Kelvin and
first published by someone else I cannot recall, says that for any
reasonably smoothly varying vector
 ,
,
where the first integral is over any smooth surface area 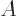 and the
second integral is over the edge of that surface. How did Stokes
get his name on it? He tortured his students with it, that’s
how!
and the
second integral is over the edge of that surface. How did Stokes
get his name on it? He tortured his students with it, that’s
how!
One important consequence of the Stokes theorem is for vector fields
 that are
that are irrotational,
i.e. that have



 0. Such fields can be written as
0. Such fields can be written as
Here 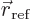 is the position of an arbitrarily chosen
reference point, usually the origin. The reason the field
is the position of an arbitrarily chosen
reference point, usually the origin. The reason the field  can be written this way is the Stokes theorem. Because of the
theorem, it does not make a difference along which path from
can be written this way is the Stokes theorem. Because of the
theorem, it does not make a difference along which path from
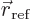 to
to 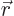 you integrate. (Any two paths give the
same answer, as long as
you integrate. (Any two paths give the
same answer, as long as  is irrotational everywhere in
between the paths.) So the definition of
is irrotational everywhere in
between the paths.) So the definition of  is unambiguous. And
you can verify that the partial derivatives of
is unambiguous. And
you can verify that the partial derivatives of  give the
components of
give the
components of  by approaching the final position
by approaching the final position 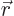 in
the integration from the corresponding direction.
in
the integration from the corresponding direction.
- symmetry
- A symmetry is an operation under which an object
does not change. For example, a human face is almost, but not
completely, mirror symmetric: it looks almost the same in a mirror
as when seen directly. The electrical field of a single point
charge is spherically symmetric; it looks the same from whatever
angle you look at it, just like a sphere does. A simple smooth
glass (like a glass of water) is cylindrically symmetric; it looks
the same whatever way you rotate it around its vertical axis.
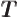
- May indicate:
- Absolute temperature. The absolute temperature in degrees K
equals the temperature in centigrade plus 273.15. When the
absolute temperature is zero, (i.e. at
 273.15
273.15  C), nature is in the state of lowest
possible energy.
C), nature is in the state of lowest
possible energy.
- Kinetic energy. A hat indicates the associated operator. The
operator is given by the Laplacian times
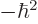 /
/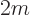 .
.
- Isospin. A hat indicates the associated operator. A vector
symbol or subscript distinguishes it from kinetic energy.
- Tesla. The unit of magnetic field strength, kg/C-s.
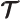
- Translation operator that translates a wave
function through space. The amount of translation is usually
indicated by a subscript.
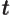
- May indicate:
- Time.
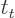 is the quantum number of square isospin.
is the quantum number of square isospin.
- temperature
- A measure of the heat motion of the particles
making up macroscopic objects. At absolute zero temperature, the
particles are in the
ground state
of lowest possible
energy.
- triple product
- A product of three vectors. There are two
different versions:
- The scalar triple product
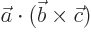 . In index notation,
. In index notation,
where 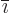 is the index following
is the index following  in the sequence
123123..., and
in the sequence
123123..., and 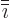 the one preceding it. This triple
product equals the determinant
the one preceding it. This triple
product equals the determinant 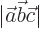 formed
with the three vectors. Geometrically, it is plus or minus the
volume of the parallelepiped that has vectors
formed
with the three vectors. Geometrically, it is plus or minus the
volume of the parallelepiped that has vectors 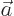 ,
,
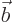 , and
, and 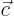 as edges. Either way, as long as the
vectors are normal vectors and not operators,
as edges. Either way, as long as the
vectors are normal vectors and not operators,
and you can change the two sides of the dot product without
changing the triple product, and/or you can change the sides in
the vectorial product with a change of sign. If any of the
vectors is an operator, use the index notation expression to work
it out.
- The vectorial triple product
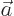

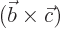 . In index notation, component number
. In index notation, component number  of this triple product is
of this triple product is
which may be rewritten as
In particular, as long as the vectors are normal ones,
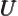
- May indicate:
- A unitary operator, in other words one that does not
change the magnitude of the wave function.
- Often used for energy, though not in this book.
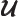
- The time shift operator:
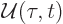 changes
the wave function
changes
the wave function 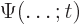 into
into 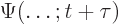 .
If the Hamiltonian is independent of time
.
If the Hamiltonian is independent of time
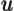
- May indicate:
- The first velocity component in a Cartesian coordinate system.
- A complex coordinate in the derivation of spherical harmonics.
- An integration variable.
- u
- May indicate the atomic mass constant, equivalent to
1.660 538 92 10
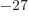 kg or 931.494 06 MeV/
kg or 931.494 06 MeV/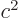 .
.
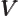
- May indicate:
- The potential energy.
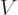 is used interchangeably for the
numerical values of the potential energy and for the operator that
corresponds to multiplying by
is used interchangeably for the
numerical values of the potential energy and for the operator that
corresponds to multiplying by 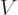 . In other words,
. In other words,
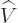 is simply written as
is simply written as 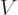 .
.
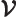
- Volume.
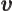
- May indicate:
- The second velocity component in a Cartesian coordinate system.
- Magnitude of a velocity (speed).
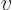 is specific volume.
is specific volume.
- A complex coordinate in the derivation of spherical harmonics.
- As
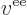 , a single electron pair potential.
, a single electron pair potential.
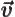
- May indicate:
- Velocity vector.
- Generic vector.
- Summation index of a lattice potential.
- vector
- Simply put, a list of numbers. A vector
 in
index notation is a set of numbers
in
index notation is a set of numbers 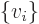 indexed by an index
indexed by an index
 . In normal three-dimensional Cartesian space,
. In normal three-dimensional Cartesian space,  takes the
values 1, 2, and 3, making the vector a list of three numbers,
takes the
values 1, 2, and 3, making the vector a list of three numbers,
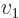 ,
, 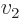 , and
, and 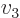 . These numbers are called the three
components of
. These numbers are called the three
components of  . The list of numbers can be visualized as a
column, and is then called a ket vector, or as a row, in which case
it is called a bra vector. This convention indicates how
multiplication should be conducted with them. A bra times a ket
produces a single number, the dot product or inner product of the
vectors:
. The list of numbers can be visualized as a
column, and is then called a ket vector, or as a row, in which case
it is called a bra vector. This convention indicates how
multiplication should be conducted with them. A bra times a ket
produces a single number, the dot product or inner product of the
vectors:
To turn a ket into a bra for purposes of taking inner products,
write the complex conjugates of its components as a row.
Formal definitions of vectors vary, but real mathematicians will
tell you that vectors are objects that can be manipulated in certain
ways (addition and multiplication by a scalar). Some physicists
define vectors as objects that transform in a certain way under
coordinate transformation (one-dimensional tensors); that is not
the same thing.
- vectorial product
- An vectorial product, or cross product is a product of vectors
that produces another vector. If
it means in index notation
that the  -th component of vector
-th component of vector 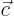 is
is
where 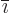 is the index following
is the index following  in the sequence 123123...,
and
in the sequence 123123...,
and 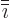 the one preceding it. For example,
the one preceding it. For example, 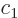 will equal
will equal
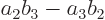 .
.
- W
- May indicate:
- Watt, the SI unit of power.
- The W
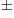 are the charged carriers of the weak force.
See also
are the charged carriers of the weak force.
See also Z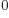 .
.
- W.u. stands for Weisskopf unit, a simple decay ballpark for
gamma decay.
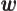
- May indicate:
- The third velocity component in a Cartesian coordinate system.
- Weight factor.
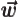
- Generic vector.
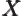
- Used in this book to indicate a function of
 to be determined.
to be determined.
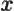
- May indicate:
- First coordinate in a Cartesian coordinate system.
- A generic argument of a function.
- An unknown value.
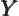
- Used in this book to indicate a function of
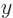 to be determined.
to be determined.
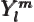
- Spherical harmonic. Eigenfunction of both
angular momentum in the
 -direction and of total square angular
momentum.
-direction and of total square angular
momentum.
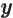
- May indicate:
- Second coordinate in a Cartesian coordinate system.
- A second generic argument of a function.
- A second unknown value.
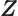
- May indicate:
- Atomic number (number of protons in the nucleus).
- Number of particles.
- Partition function.
- The Z
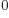 is the uncharged carrier of the weak force. See
also
is the uncharged carrier of the weak force. See
also W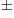 .
.
- Used in this book to indicate a function of
 to be
determined.
to be
determined.
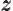
- May indicate:
- Third coordinate in a Cartesian coordinate system.
- A third generic argument of a function.
- A third unknown value.
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
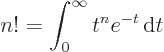
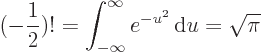
![]()
![]()
![]()
![]()
![]()
![]() /
/![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.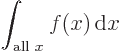
![]()
![]() .
.![]()
![]() .
.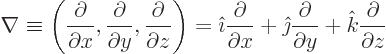
![]()
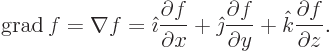
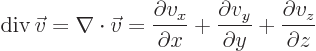
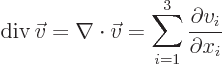
![]() -
-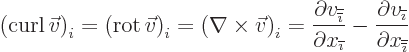
![]()
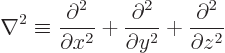
![]() ,
,![]()
![]() .
.![]()
![]()
![]() -
-![]()
![]()
![]()
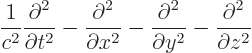
![]() 1
1![]() .
.![]() /
/![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
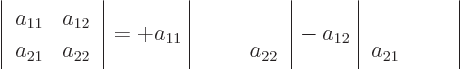
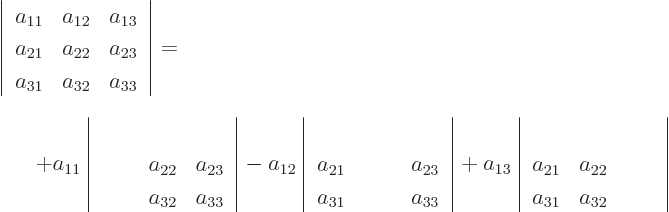
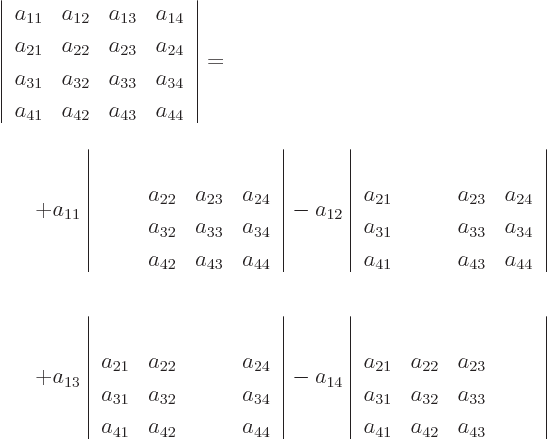
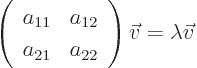
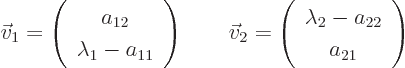
.
![]()
![]()
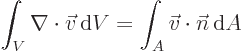
![]()
![]()
![]() -
-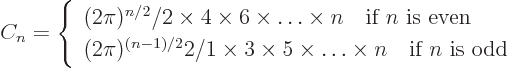
![]() -
-![]()
![]() )
)![]()
![]() ,
,![]() ,
,![]() ,
,![]() :
: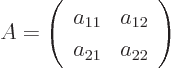
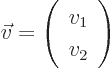
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
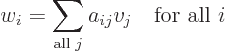
![]()
![]()
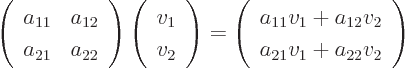
![]()
![]()
![]()
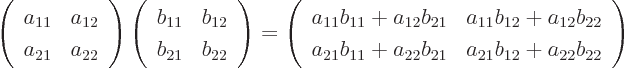
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,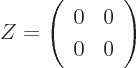
![]() ,
,![]()
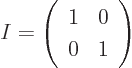
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
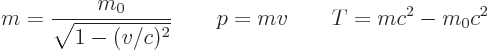
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ;
;![]()
![]() ,
,![]() ,
,![]()
![]()
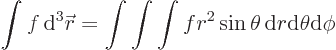
![]()
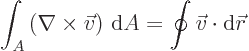
![]()
![]()
![]()
![]()
![]()
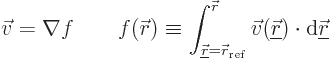
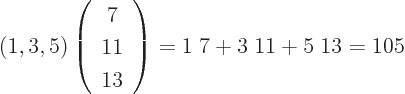
.
.