|
|
|
|
|
Next: A.2 An example of variational calculus |
|
Lagrangian mechanics is a way to simplify complicated dynamical problems. This note gives a brief overview. For details and practical examples you will need to consult a good book on mechanics.
As a trivial example of how Lagrangian mechanics works, consider a simple molecular dynamics simulation. Assume that the forces on the particles are given by a potential that only depends on the positions of the particles.
The difference between the net kinetic energy and the net potential
energy is called the “Lagrangian.” For a system of particles as considered here it
takes the form
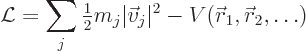
It is important to note that in Lagrangian dynamics, the Lagrangian must mathematically be treated as a function of the velocities and positions of the particles. While for a given motion, the positions and velocities are in turn a function of time, time derivatives must be implemented through the chain rule, i.e. by means of total derivatives of the Lagrangian.
The canonical momentum
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
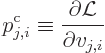
The Lagrangian equations of motion are
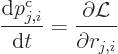
One place where Lagrangian dynamics is very helpful is for macroscopic
objects. Consider for example the dynamics of a Frisbee. Nobody is
going to do a molecular dynamics computation of a Frisbee. What you
do is approximate the thing as a solid body,
(or more
accurately, a rigid body). The position of every part of a solid body
can be fully determined using only six parameters, instead of the
countless position coordinates of the individual atoms. For example,
knowing the three position coordinates of the center of gravity of the
Frisbee and three angles is enough to fully fix it. Or you could just
choose three reference points on the Frisbee: giving three position
coordinates for the first point, two for the second, and one for the
third is another possible way to fix its position.
Such parameters that fix a system are called “generalized coordinates.” The word generalized indicates that they do not need to be Cartesian coordinates; often they are angles or distances, or relative coordinates or angles. The number of generalized coordinates is called the number of degrees of freedom. It varies with the system. A bunch of solid bodies moving around freely will have six per solid body; but if there are linkages between them, like the bars in your car’s suspension system, it reduces the number of degrees of freedom. A rigid wheel spinning around a fixed axis has only one degree of freedom, and so does a solid pendulum swinging around a fixed axis. Attach a second pendulum to its end, maybe not in the same plane, and the resulting compound pendulum has two degrees of freedom.
If you try to describe such systems using plain old Newtonian mechanics, it can get ugly. For each solid body you can apply that the sum of the forces must equal mass times acceleration of the center of gravity, and that the net moment around the center of gravity must equal the rate of change of angular momentum, which you then presumably deduce using the principal axis system.
Instead of messing with all that complex vector algebra, Lagrangian dynamics allows you to deal with just a single scalar, the Lagrangian. If you can merely figure out the net kinetic and potential energy of your system in terms of your generalized coordinates and their time derivatives, you are in business.
If there are linkages between the members of the system, the benefits magnify. A brute-force Newtonian solution of the three-dimensional compound pendulum would involve six linear momentum equations and six angular ones. Yet the thing has only two degrees of freedom; the angular orientations of the individual pendulums around their axes of rotation. The reason that there are twelve equations in the Newtonian approach is that the support forces and moments exerted by the two axes add another 10 unknowns. A Lagrangian approach allows you to just write two equations for your two degrees of freedom; the support forces do not appear in the story. That provides a great simplification.
This section describes the Lagrangian approach to dynamics in general.
Assume that you have chosen suitable generalized coordinates that
fully determine the state of your system. Call these generalized
coordinates ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
Now find the kinetic energy ![]()
![]()
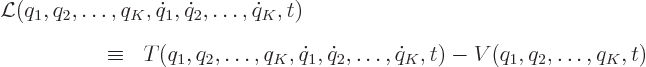
The canonical momenta are defined as
The ![]()
![]() .
.![]()
![]()
![]() .
.virtual displacement.
During such a
displacement, each force that is not modelled by ![]()
![]()
![]() .
.
The bottom line is that normally the ![]()
![]()
It may be noted that in relativistic mechanics, the Lagrangian is not the difference between potential and kinetic energy. However, the Lagrangian equations of motion (A.1) and (A.2) still apply.
The general concept that applies both nonrelativistically and
relativistically is that of “action.” The action ![]()
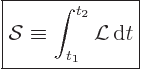 |
(A.3) |
See {D.3.1} for a derivation of the above claims.
For a system with ![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
However, there is a much neater way to get ![]()
![]()
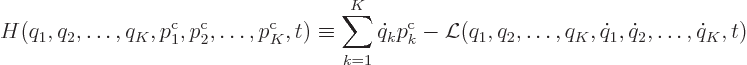 |
(A.4) |
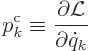
In terms of the Hamiltonian, the equations of motion are
If the Hamiltonian does not explicitly depend on time and the generalized forces are zero, these evolution equations imply that the Hamiltonian does not change with time at all. For such systems, the Hamiltonian is the conserved total energy of the system. In particular for a nonrelativistic system, the Hamiltonian is the sum of the kinetic and potential energies, provided that the position of the system only depends on the generalized coordinates and not also explicitly on time.
See {D.3.2} for a derivation of the above claims.
The previous subsections discussed discrete mechanical objects like molecules, Frisbees, and pendulums. However, the Lagrangian and Hamiltonian formalisms can be generalized to fields like the electromagnetic field. That is mainly important for advanced physics like quantum field theories; these are not really covered in this book. But since it does appear in one advanced addendum, {A.22}, this subsection will summarize the main points.
The simplest classical field is the electrostatic potential
![]() .
.![]() ,
,![]()
![]()
In addition there may be discrete variables. Electromagnetics would
be pretty boring if you would not have some charged particles around.
A generic coordinate of such a particle will be indicated as
![]() .
.![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]() .
.
Under the above conditions, the Lagrangian will involve an integral:
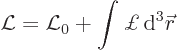
The first part ![]()
The Lagrangian density ![]()
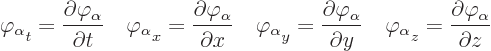
This brings up one practical point. Consider a contribution such as
the potential energy of a particle called ![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.
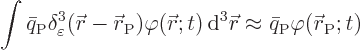
The Lagrangian equations for the discrete parameters are exactly the
same as before, but of course now the Lagrangian includes the
integral, {D.3.3}:
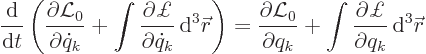 |
(A.6) |
The Lagrangian equations for the field are based on the Lagrangian
density instead of the Lagrangian itself. That is why you really want
to have the terms involving the field as integrals. The equations are
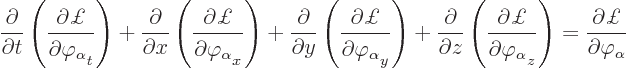 |
(A.7) |
The canonical momenta are now
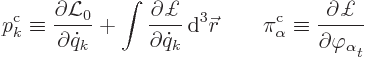 |
(A.8) |
The Hamiltonian is
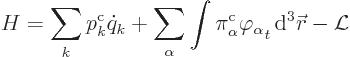 |
(A.9) |
Hamilton’s equations for discrete variables are as before:
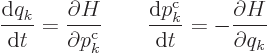 |
(A.10) |
The equations for the fields are a bit tricky. If there are no
discrete variables, there is no problem. Then the Hamiltonian can be
written in terms of a Hamiltonian density ![]()
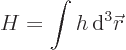
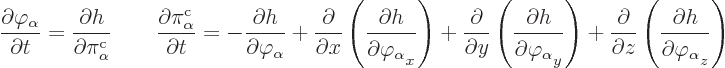
Unfortunately, if there are discrete parameters, products of integrals
will appear. Then there is no Hamiltonian density. So the only thing
you can do do is differentiate the full Hamiltonian ![]()
![]() .
.![]()
![]() .
.![]()
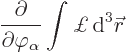
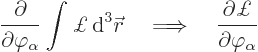
See {D.3.3} for a justification of this procedure and the other claims in this subsection.