| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.2 An example of variational calculus
The problem to solve in addendum {A.22.1} provides a simple
example of variational calculus.
The problem can be summarized as follows. Given is the following
expression for the net energy of a system:
Here the operator  is defined as
is defined as
The integrals are over all space, or over some other given region.
Further 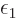 is assumed to be a given positive constant and
is assumed to be a given positive constant and
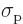

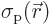 is a given function of
the position
is a given function of
the position  . The function
. The function 

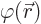 will be called the potential and is not given. Obviously the energy
depends on what this potential is. Mathematicians would say that
will be called the potential and is not given. Obviously the energy
depends on what this potential is. Mathematicians would say that  is a “functional,” a number that depends on what a function is.
is a “functional,” a number that depends on what a function is.
The energy  will be minimal for some specific potential
will be minimal for some specific potential
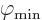 . The objective is now to find an equation
for this potential
. The objective is now to find an equation
for this potential 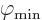 using variational calculus.
using variational calculus.
To do so, the basic idea is the following: imagine that you start at
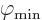 and then make an infinitesimally small change
and then make an infinitesimally small change
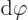 to it. In that case there should be no change
to it. In that case there should be no change 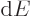 in energy. After all, if there was an negative change in
in energy. After all, if there was an negative change in  , then
, then
 would decrease. That would contradict that
would decrease. That would contradict that 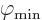 produces the lowest energy of all. If there was an positive
infinitesimal change in
produces the lowest energy of all. If there was an positive
infinitesimal change in  , then a change in potential of opposite
sign would give a negative change in
, then a change in potential of opposite
sign would give a negative change in  . Again that produces a
contradiction to what is given.
. Again that produces a
contradiction to what is given.
The typical physicist would now work out the details as follows. The
slightly perturbed potential is written as
Note that the 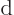 in
in 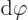 has been renotated as
has been renotated as
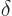 . That is because everyone does so in variational
calculus. The symbol does not make a difference, the idea remains the
same. Note also that
. That is because everyone does so in variational
calculus. The symbol does not make a difference, the idea remains the
same. Note also that 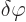 is a function of position; the
change away from
is a function of position; the
change away from 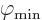 is normally different at
different locations. You are in fact allowed to choose anything you
like for the function
is normally different at
different locations. You are in fact allowed to choose anything you
like for the function 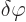 , as long as it is
sufficiently small and it is zero at the limits of integration.
, as long as it is
sufficiently small and it is zero at the limits of integration.
Now just take differentials like you typically do it in calculus or
physics. If in calculus you had some expression like 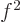 , you
would say
, you
would say 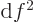

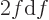 . (For example, if
. (For example, if  is
a function of a variable
is
a function of a variable 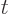 , then
, then 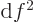

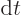

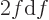

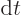 . But physicists usually do not bother with
the
. But physicists usually do not bother with
the 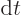 ; then they do not have to worry what exactly
; then they do not have to worry what exactly  is
a function of.) Similarly
is
a function of.) Similarly
where
so
For a change starting from 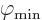 :
:
(Note that  by itself gets approximated as
by itself gets approximated as
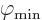 , but
, but 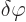 is the completely
arbitrary change that can be anything.) Also,
is the completely
arbitrary change that can be anything.) Also,
because 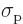 is a given constant at every position.
is a given constant at every position.
Total you get for the change in energy that must be zero
A conscientious mathematician would shudder at the above
manipulations. And for good reason. Small changes are not good
mathematical concepts. There is no such thing as
small
in mathematics. There are just limits where
things go to zero. What a mathematician would do instead is write the
change in potential as a some multiple 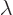 of a chosen function
of a chosen function
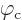 . So the changed potential is written as
. So the changed potential is written as
The chosen function 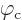 can still be anything that you
want that vanishes at the limits of integration. But it is not
assumed to be
can still be anything that you
want that vanishes at the limits of integration. But it is not
assumed to be small.
So now no mathematical nonsense
is written. The energy for this changed potential is
Now this energy is a function of the multiple 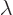 . And
that is a simple numerical variable. The energy must be smallest at
. And
that is a simple numerical variable. The energy must be smallest at
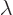 = 0, because
= 0, because 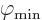 gives the minimum energy.
So the above function of
gives the minimum energy.
So the above function of 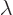 must have a minimum at
must have a minimum at 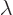
 0. That means that it must have a zero derivative at
0. That means that it must have a zero derivative at 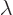
 0. So just differentiate the expression with respect to
0. So just differentiate the expression with respect to
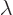 . (You can differentiate as is, or simplify first and
bring
. (You can differentiate as is, or simplify first and
bring 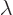 outside the integrals.) Set this derivative to zero
at
outside the integrals.) Set this derivative to zero
at 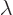
 0. That gives the same result (2) as derived by
physicists, except that
0. That gives the same result (2) as derived by
physicists, except that 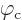 takes the place of
takes the place of
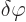 . The result is the same, but the derivation is
nowhere fishy.
. The result is the same, but the derivation is
nowhere fishy.
This derivation will return to the notations of physicists. The next
step is to get rid of the derivatives on 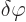 . Note
that
. Note
that
The way to get rid of the derivatives on 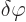 is by
integration by parts. Integration by parts pushes a derivative from
one factor on another. Here you see the real reason why the changes
in potential must vanish at the limits of integration. If they did
not, integrations by parts would bring in contributions from the
limits of integration. That would be a mess.
is by
integration by parts. Integration by parts pushes a derivative from
one factor on another. Here you see the real reason why the changes
in potential must vanish at the limits of integration. If they did
not, integrations by parts would bring in contributions from the
limits of integration. That would be a mess.
Integrations by parts of the three terms in the integral in the
 ,
,  , and
, and  directions respectively produce
directions respectively produce
In vector notation, that becomes
Substituting that in the change of energy (2) gives
The final step is to say that this can only be true for whatever
change 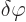 you take if the parenthetical expression is
zero. That gives the final looked-for equation for
you take if the parenthetical expression is
zero. That gives the final looked-for equation for
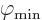 :
:
To justify the above final step, call the parenthetical expression  for short. Then the variational statement above is of the form
for short. Then the variational statement above is of the form
where 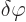 can be arbitrarily chosen as long as it is zero
at the limits of integration. It is now to be shown that this implies
that
can be arbitrarily chosen as long as it is zero
at the limits of integration. It is now to be shown that this implies
that  is everywhere zero inside the region of integration.
is everywhere zero inside the region of integration.
(Note here that whatever function  is, it should not contain
is, it should not contain
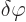 . And there should not be any derivatives of
. And there should not be any derivatives of
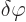 anywhere at all. Otherwise the above statement is not
valid.)
anywhere at all. Otherwise the above statement is not
valid.)
The best way to see that  must be zero everywhere is first assume
the opposite. Assume that
must be zero everywhere is first assume
the opposite. Assume that  is nonzero at some point P. In that
case select a function
is nonzero at some point P. In that
case select a function 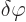 that is zero everywhere except
in a small vicinity of P, where it is positive. (Make sure the
vicinity is small enough that
that is zero everywhere except
in a small vicinity of P, where it is positive. (Make sure the
vicinity is small enough that  does not change sign in it.) Then
the integral above is nonzero; in particular, it will have the same
sign as
does not change sign in it.) Then
the integral above is nonzero; in particular, it will have the same
sign as  at P. But that is a contradiction, since the integral
must be zero. So the function
at P. But that is a contradiction, since the integral
must be zero. So the function  cannot be nonzero at a point P; it
must be zero everywhere.
cannot be nonzero at a point P; it
must be zero everywhere.
(There are more sophisticated ways to do this. You could take
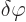 as a positive multiple of
as a positive multiple of  that fades away to zero
away from point P. In that case the integral will be positive unless
that fades away to zero
away from point P. In that case the integral will be positive unless
 is everywhere zero. And sign changes in
is everywhere zero. And sign changes in  are no longer a
problem.)
are no longer a
problem.)
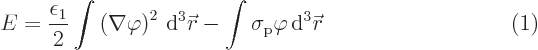
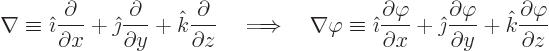
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() .
.![]() ,
,![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ;
;![]()
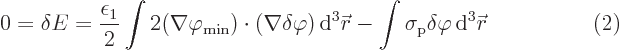
![]()
![]() .
.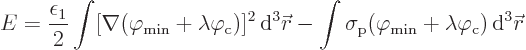
![]() .
.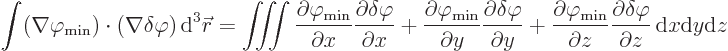
![]() ,
,![]() ,
,![]()
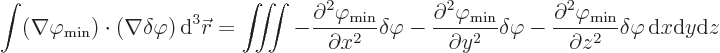
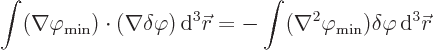
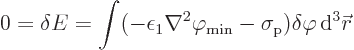
![]()
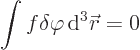
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()