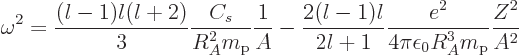| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
A.43 Classical vibrating drop
The simplest collective description for a nucleus models it as a
vibrating drop of a macroscopic liquid. To represent the nuclear
Coulomb repulsions the liquid can be assumed to be positively charged.
This section gives a condensed derivation of small vibrations of such
a liquid drop according to classical mechanics. It will be a pretty
elaborate affair, condensed or not.
A.43.1 Basic definitions
The drop is assumed to be a sphere of radius  when it is not
vibrating. For a nucleus,
when it is not
vibrating. For a nucleus,  can be identified as the nuclear
radius,
can be identified as the nuclear
radius,
When vibrating, the radial position of the surface will be indicated
by 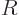 . This radial position will depend on the spherical
angular coordinates
. This radial position will depend on the spherical
angular coordinates 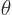 and
and 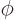 , figure
N.3, and time.
, figure
N.3, and time.
The mass density, (mass per unit volume), of the liquid will be
indicated by 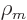 . Ignoring the difference between proton
and neutron mass, for a nucleus the mass density can be identified as
. Ignoring the difference between proton
and neutron mass, for a nucleus the mass density can be identified as
The mass density is assumed constant throughout the drop. This
implies that the liquid is assumed to be incompressible, meaning that
the volume of any chunk of liquid is unchangeable.
The charge density is defined analogously to the mass density:
It too is assumed constant.
The surface tension 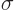 can be identified as
can be identified as
A.43.2 Kinetic energy
The possible frequencies of vibration can be figured out from the
kinetic and potential energy of the droplet. The kinetic energy is
easiest to find and will be done first.
As noted, the liquid will be assumed to be incompressible. To see
what that means for the motion, consider an arbitrary chunk of liquid.
An elementary element of surface area 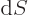 of that chunk gobbles
up an amount of volume while it moves given by
of that chunk gobbles
up an amount of volume while it moves given by
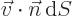 , where
, where 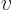 is the liquid velocity and
is the liquid velocity and
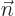 is a unit vector normal to the surface. But for a given chunk
of an incompressible liquid, the total volume cannot change.
Therefore:
is a unit vector normal to the surface. But for a given chunk
of an incompressible liquid, the total volume cannot change.
Therefore:
Using the Gauss-Ostrogradsky, or divergence theorem, this means that
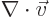 must integrate to zero over the interior of the
chunk of liquid. And if it must integrate to zero for whatever you
take the chunk to be, it must be zero uniformly:
must integrate to zero over the interior of the
chunk of liquid. And if it must integrate to zero for whatever you
take the chunk to be, it must be zero uniformly:
This is the famous “continuity equation” for incompressible flow. But it is really
no different from Maxwell’s continuity equation for the flow of
charges if the charge density remains constant, chapter
13.2.
To describe the dynamics of the drop, the independent variables will
be taken to be time and the unperturbed positions 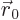 of
the infinitesimal volume elements
of
the infinitesimal volume elements 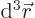 of liquid. The velocity
field inside the drop is governed by Newton’s second law. On a
unit volume basis, this law takes the form
of liquid. The velocity
field inside the drop is governed by Newton’s second law. On a
unit volume basis, this law takes the form
where 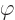 is the electrostatic potential and
is the electrostatic potential and 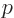 is the
pressure. It will be assumed that the motion is slow enough that
electrostatics may be used for the electromagnetic force. As far as
the pressure force is concerned, it is one of the insights obtained in
classical fluid mechanics that a constant pressure acting equally from
all directions on a volume element of liquid does not produce a net
force. To get a net force on an element of liquid, the pressure force
on the front of the element pushing it back must be different from the
one on the rear pushing it forward. So there must be variations in
pressure to get a net force on elements of liquid. Using that idea, it
can be shown that for an infinitesimal element of liquid, the net
force per unit volume is minus the gradient of pressure. For a real
classical liquid, there may also be viscous internal forces in addition
to pressure forces. However, viscosity is a macroscopic effect that
is not relevant to the nuclear quantum system of interest here. (That
changes in a two-liquid description,
[40, p. 187].)
is the
pressure. It will be assumed that the motion is slow enough that
electrostatics may be used for the electromagnetic force. As far as
the pressure force is concerned, it is one of the insights obtained in
classical fluid mechanics that a constant pressure acting equally from
all directions on a volume element of liquid does not produce a net
force. To get a net force on an element of liquid, the pressure force
on the front of the element pushing it back must be different from the
one on the rear pushing it forward. So there must be variations in
pressure to get a net force on elements of liquid. Using that idea, it
can be shown that for an infinitesimal element of liquid, the net
force per unit volume is minus the gradient of pressure. For a real
classical liquid, there may also be viscous internal forces in addition
to pressure forces. However, viscosity is a macroscopic effect that
is not relevant to the nuclear quantum system of interest here. (That
changes in a two-liquid description,
[40, p. 187].)
Note that the gradients of the potential and pressure should normally
be evaluated with respect to the perturbed position coordinates
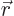 . But if the amplitude of vibrations is infinitesimally
small, it is justified to evaluate
. But if the amplitude of vibrations is infinitesimally
small, it is justified to evaluate  using the unperturbed
position coordinates
using the unperturbed
position coordinates 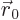 instead. Similarly,
instead. Similarly,  in the
continuity equation can be taken to be with respect to the unperturbed
coordinates.
in the
continuity equation can be taken to be with respect to the unperturbed
coordinates.
If you take the divergence of Newton’s equation. i.e. multiply
with  , the left hand side vanishes because of
continuity, and so the sum of potential and pressure satisfies the
so-called “Laplace equation:”
, the left hand side vanishes because of
continuity, and so the sum of potential and pressure satisfies the
so-called “Laplace equation:”
The solution can be derived in spherical coordinates 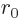 ,
,
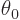 , and
, and 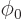 using similar, but simpler, techniques
as used to solve the hydrogen atom. The solution takes the form
using similar, but simpler, techniques
as used to solve the hydrogen atom. The solution takes the form
where the 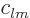 are small unknown coefficients and the
are small unknown coefficients and the
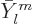 are real spherical harmonics. The precise form of the
are real spherical harmonics. The precise form of the
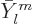 is not of importance in the analysis.
is not of importance in the analysis.
Plugging the solution for the pressure into Newton’s second law
shows that the velocity can be written as
where the coefficients 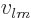 are multiples of time integrals of the
are multiples of time integrals of the
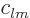 . What multiples is irrelevant as the potential and
pressure will no longer be used.
. What multiples is irrelevant as the potential and
pressure will no longer be used.
(You might wonder about the integration constant in the time
integration. It is assumed that the droplet was initially spherical
and at rest before some surface perturbation put it into motion. If
the drop was initially rotating, the analysis here would need to be
modified. More generally, if the droplet was not at rest initially,
it must be assumed that the initial velocity is “irrotational,” meaning that 
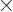

 0.)
0.)
Since the velocity is the time-derivative of position, the positions
of the fluid elements are
where 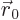 is the unperturbed position of the fluid element and
the coefficients of velocity are related to those of position by
is the unperturbed position of the fluid element and
the coefficients of velocity are related to those of position by
What will be important in the coming derivations is the radial
displacement of the liquid surface away from the spherical shape. It
follows from taking the radial component of the displacement evaluated
at the surface 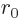

 . That produces
. That produces
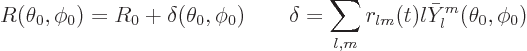 |
(A.266) |
To be sure, in the analysis  will be defined to be the radial
surface displacement as a function of the physical angles
will be defined to be the radial
surface displacement as a function of the physical angles 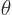 and
and
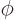 . However, the difference between physical and
unperturbed angles can be ignored because the perturbations are
assumed to be infinitesimal.
. However, the difference between physical and
unperturbed angles can be ignored because the perturbations are
assumed to be infinitesimal.
The kinetic energy is defined by
Putting in the expression for the velocity field in terms of the
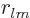 position coefficients gives
position coefficients gives
To simplify this, a theorem is useful. If any two functions 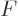 and
and
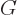 are solutions of the Laplace equation, then the integral of their
gradients over the volume of a sphere can be simplified to an integral
over the surface of that sphere:
are solutions of the Laplace equation, then the integral of their
gradients over the volume of a sphere can be simplified to an integral
over the surface of that sphere:
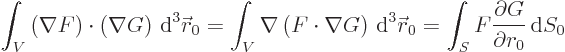 |
(A.267) |
The first equality is true because the first term obtained in
differentiating out the product 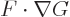 is the left hand
side, while the second term is zero because
is the left hand
side, while the second term is zero because 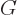 satisfies the Laplace
equation. The second equality is the divergence theorem applied to
the sphere. Further, the surface element of a sphere is in spherical
coordinates:
satisfies the Laplace
equation. The second equality is the divergence theorem applied to
the sphere. Further, the surface element of a sphere is in spherical
coordinates:
Applying these results to the integral for the kinetic energy, noting
that 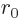

 on the surface of the droplet, gives
on the surface of the droplet, gives
Now the spherical harmonics are orthonormal on the unit sphere; that
means that the final integral is zero unless 

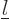 and
and 

 , and in that case the integral is one. Therefore,
the final expression for the kinetic energy becomes
, and in that case the integral is one. Therefore,
the final expression for the kinetic energy becomes
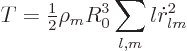 |
(A.268) |
A.43.3 Energy due to surface tension
From here on, the analysis will return to physical coordinates rather
than unperturbed ones.
The potential energy due to surface tension is simply the surface
tension times the surface of the deformed droplet. To evaluate that,
first an expression for the surface area of the droplet is needed.
The surface can be described using the spherical angular coordinates
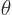 and
and 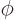 as
as 

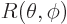 . An
infinitesimal coordinate element
. An
infinitesimal coordinate element 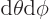 corresponds to a
physical surface element that is approximately a parallelogram.
Specifically, the sides of that parallelogram are
corresponds to a
physical surface element that is approximately a parallelogram.
Specifically, the sides of that parallelogram are
To get the surface area 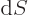 , take a vectorial product of
these two vectors and then the length of that. To work it out, note
that in terms of the orthogonal unit vectors of a spherical coordinate
system,
, take a vectorial product of
these two vectors and then the length of that. To work it out, note
that in terms of the orthogonal unit vectors of a spherical coordinate
system,
That way, the surface area works out to be
Multiply by the surface tension 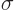 and you have the potential
energy due to surface tension.
and you have the potential
energy due to surface tension.
Of course, this expression is too complicated to work with. What
needs to be done, first of all, is to write the surface in the form
where  is the small deviation away from the radius
is the small deviation away from the radius  of a
perfect spherical drop. This can be substituted into the integral,
and the integrand can then be expanded into a Taylor series in terms
of
of a
perfect spherical drop. This can be substituted into the integral,
and the integrand can then be expanded into a Taylor series in terms
of  . That gives the potential energy
. That gives the potential energy 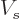

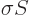 as
as
where the final integral comes from expanding the square root and
where terms of order of magnitude 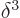 or less have been
ignored. The first integral in the result can be ignored; it is the
potential energy of the undeformed droplet, and only differences in
potential energy are important. However, the second integral is one
problem, and the final one another.
or less have been
ignored. The first integral in the result can be ignored; it is the
potential energy of the undeformed droplet, and only differences in
potential energy are important. However, the second integral is one
problem, and the final one another.
The second integral is first. Its problem is that if you plug in a
valid approximate expression for  , you are still not
going to get a valid approximate result for the integral. The radial
deformation
, you are still not
going to get a valid approximate result for the integral. The radial
deformation  is both negative and positive over the surface of
the cylinder, and if you integrate, the positive parts integrate away
against the negative parts, and what you have left is mainly the
errors.
is both negative and positive over the surface of
the cylinder, and if you integrate, the positive parts integrate away
against the negative parts, and what you have left is mainly the
errors.
Why is  both positive and negative? Because the volume of the
liquid must stay the same, and if
both positive and negative? Because the volume of the
liquid must stay the same, and if  was all positive, the volume
would increase. The condition that the volume must remain the same
means that
was all positive, the volume
would increase. The condition that the volume must remain the same
means that
the first because of the expression for volume in spherical
coordinates and the second from integrating out  . Writing
again
. Writing
again 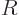

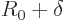 and expanding in a Taylor series gives
after rearranging
and expanding in a Taylor series gives
after rearranging
where the integral of 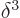 has been ignored. Now the integral
in the left hand side is essentially the one needed in the potential
energy. According to this equation, it can be replaced by the
integral in the right hand side. And that one can be accurately
evaluated using an approximate expression for
has been ignored. Now the integral
in the left hand side is essentially the one needed in the potential
energy. According to this equation, it can be replaced by the
integral in the right hand side. And that one can be accurately
evaluated using an approximate expression for  : since
the integrand is all positive, there is no cancellation that leaves
only the errors. Put more precisely, if the used expression for
: since
the integrand is all positive, there is no cancellation that leaves
only the errors. Put more precisely, if the used expression for
 has an error of order
has an error of order 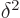 , direct evaluation of
the integral in the left hand side gives an unacceptable error of
order
, direct evaluation of
the integral in the left hand side gives an unacceptable error of
order 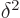 , but evaluation of the integral in the right
hand side gives an acceptable error of order
, but evaluation of the integral in the right
hand side gives an acceptable error of order 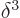 .
.
If this is used in the expression for the potential energy, it
produces
Now  can be written in terms of the spherical harmonics
defined in the previous subsection as
can be written in terms of the spherical harmonics
defined in the previous subsection as
where the 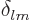 are time dependent coefficients still to be
found. If this is substituted into the expression for the potential,
the first integral is similar to the one encountered in the previous
subsection; it is given by the orthonormality of the spherical
harmonics. However, the final term involves an integral of the form
are time dependent coefficients still to be
found. If this is substituted into the expression for the potential,
the first integral is similar to the one encountered in the previous
subsection; it is given by the orthonormality of the spherical
harmonics. However, the final term involves an integral of the form
This integral can be simplified by using the same theorem
(A.267) used earlier for the kinetic energy. Just take 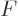

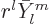 and
and 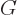

 and
integrate over a sphere of unit radius. The theorem then produces an
equality between a volume integral and a surface one. The surface
integral can be evaluated using the orthonormality of the spherical
harmonics. The volume integral can be integrated explicitly in the
radial direction to produce a multiple of
and
integrate over a sphere of unit radius. The theorem then produces an
equality between a volume integral and a surface one. The surface
integral can be evaluated using the orthonormality of the spherical
harmonics. The volume integral can be integrated explicitly in the
radial direction to produce a multiple of  above and a second term
that can once more be evaluated using the orthonormality of the
spherical harmonics. It is then seen that
above and a second term
that can once more be evaluated using the orthonormality of the
spherical harmonics. It is then seen that 
 0 unless
0 unless 

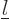 and
and 

 and then
and then 

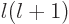 .
.
Putting it all together, the potential energy due to surface tension
becomes
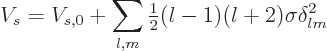 |
(A.269) |
A.43.4 Energy due to Coulomb repulsion
The potential energy due to the Coulomb forces is tricky. You need to
make sure that the derivation is accurate enough. What is needed is
the change in potential energy when the radial position of the surface
of the droplet changes from the spherical value 

 to the
slightly perturbed value
to the
slightly perturbed value 

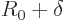 . The change in
potential energy must be accurate to the order of magnitude of
. The change in
potential energy must be accurate to the order of magnitude of
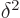 .
.
Trying to write a six-dimensional integral for the Coulomb energy would be
a mess. Instead, assume that the surface perturbation is applied in
small increments, as a perturbation  that is gradually
increased from zero to
that is gradually
increased from zero to  . Imagine that you start with
the perfect sphere and cumulatively add thin layers of charged liquid
. Imagine that you start with
the perfect sphere and cumulatively add thin layers of charged liquid
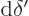 until the full surface perturbation
until the full surface perturbation  is achieved.
(With adding negative amounts
is achieved.
(With adding negative amounts 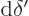 understood as removing
charged liquid. At each stage, just as much liquid is removed as
added, so that the total volume of liquid stays the same.) The change
in potential energy due to addition of an infinitesimal amount of
charge equals the amount of charge times the surface potential at the
point where it is added.
understood as removing
charged liquid. At each stage, just as much liquid is removed as
added, so that the total volume of liquid stays the same.) The change
in potential energy due to addition of an infinitesimal amount of
charge equals the amount of charge times the surface potential at the
point where it is added.
The surface radius perturbation and its differential change can be
written in terms of spherical harmonics:
The amount of charge added per unit solid angle 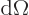

 will be called
will be called  . It is
given in terms of the charge density
. It is
given in terms of the charge density 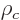 and
and  as
as
To first approximation, the incremental amount of charge laid down per
unit solid angle is
However, if 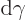 is written in terms of spherical harmonics,
is written in terms of spherical harmonics,
then the coefficient 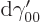 is zero exactly, because the
net volume, and hence the net charge, remains unchanged during the
build-up process. (The spherical harmonic
is zero exactly, because the
net volume, and hence the net charge, remains unchanged during the
build-up process. (The spherical harmonic 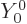 is independent of
angular position and gives the average; the average charge added must
be zero if the net charge does not change.) The coefficient
is independent of
angular position and gives the average; the average charge added must
be zero if the net charge does not change.) The coefficient
 is zero to good approximation, but not exactly.
is zero to good approximation, but not exactly.
Now the surface potential is needed for the deformed drop. There are
two contributions to this potential: the potential of the original
spherical drop and the potential of the layer  of liquid that
has been laid down, (the removed liquid here counting as negative
charge having been laid down.) For the spherical drop, to the
needed accuracy
of liquid that
has been laid down, (the removed liquid here counting as negative
charge having been laid down.) For the spherical drop, to the
needed accuracy
For the surface potential of the laid-down layer, fortunately only a
leading order approximation is needed. That means that the thickness
of the layer can be ignored. That turns it into a spherical shell of
negligible thickness at 

 . The potential inside
the shell can always be written in the form
. The potential inside
the shell can always be written in the form
though the coefficients 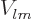 are still unknown. The potential
outside the shell takes the form
are still unknown. The potential
outside the shell takes the form
where the coefficients 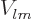 are approximately the same as those
inside the shell because the shell is too thin for the potential
to vary significantly across it.
are approximately the same as those
inside the shell because the shell is too thin for the potential
to vary significantly across it.
However, the electric field strength does vary significantly from one
side of the shell to the other, and it is that variation that
determines the coefficients 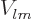 . First, integrate
Maxwell’s first equation over a small surface element of the
shell. Since the shell has thickness
. First, integrate
Maxwell’s first equation over a small surface element of the
shell. Since the shell has thickness  , you get
, you get
where 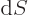 is the area of the shell element. Note that
is the area of the shell element. Note that 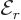

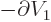

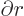 , and substitute in the
inside and outside expressions for
, and substitute in the
inside and outside expressions for 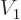 above, differentiated with
respect to
above, differentiated with
respect to  and evaluated at
and evaluated at 

 . That gives the
. That gives the
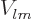 and then
and then
Multiplying the two surface potentials by the amount of charge laid
down gives the incremental change in Coulomb potential of the drop
as
Substituting in 

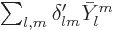 and
and 

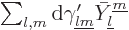 , the integrals
can be evaluated using the orthonormality of the spherical harmonics.
In particular, the first term of the surface potential integrates away
since it is independent of angular position, therefore proportional to
, the integrals
can be evaluated using the orthonormality of the spherical harmonics.
In particular, the first term of the surface potential integrates away
since it is independent of angular position, therefore proportional to
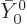 , and
, and 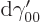 is zero. For the other
terms, it is accurate enough to set
is zero. For the other
terms, it is accurate enough to set 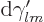

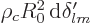 and then
and then  can be integrated from
zero to
can be integrated from
zero to  to give the Coulomb potential of the fully deformed
sphere:
to give the Coulomb potential of the fully deformed
sphere:
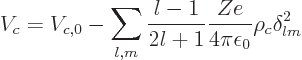 |
(A.270) |
A.43.5 Frequency of vibration
Having found the kinetic energy, (A.268), and the potential
energy, (A.269) plus (A.270), the motion of the drop
can be determined.
A rigorous analysis would so using a Lagrangian analysis,
{A.1}. It would use the coefficients 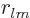 as
generalized coordinates, getting rid of the
as
generalized coordinates, getting rid of the 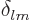 in the
potential energy terms using (A.266). But this is a bit of
an overkill, since the only thing that the Lagrangian analysis really
does is show that each coefficient
in the
potential energy terms using (A.266). But this is a bit of
an overkill, since the only thing that the Lagrangian analysis really
does is show that each coefficient 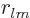 evolves completely
independent of the rest.
evolves completely
independent of the rest.
If you are willing to take that for granted, just assume 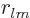

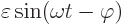 with
with 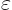 and
and
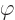 unimportant constants, and then equate the maximum kinetic
energy to the maximum potential energy to get
unimportant constants, and then equate the maximum kinetic
energy to the maximum potential energy to get 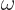 . The
result is
. The
result is
Note that this is zero if 
 0. There cannot be any vibration of
a type
0. There cannot be any vibration of
a type 

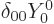 because that would be a uniform
radial expansion or compression of the drop, and its volume must
remain constant. The frequency is also zero for
because that would be a uniform
radial expansion or compression of the drop, and its volume must
remain constant. The frequency is also zero for 
 1. In that
case, the potential energy does not change according to the derived
expressions. If kinetic energy cannot be converted into potential
energy, the droplet must keep moving. Indeed, solutions for
1. In that
case, the potential energy does not change according to the derived
expressions. If kinetic energy cannot be converted into potential
energy, the droplet must keep moving. Indeed, solutions for 
 1
describe that the droplet is translating at a constant speed without
deformation. Vibrations occur for
1
describe that the droplet is translating at a constant speed without
deformation. Vibrations occur for 
 2, and the most
important ones are the ones with the lowest frequency, which means
2, and the most
important ones are the ones with the lowest frequency, which means  = 2.
= 2.
![]()
![]()
![]() .
.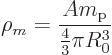
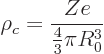
![]()
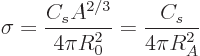
![]()
![]() ,
,![]()
![]()

![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,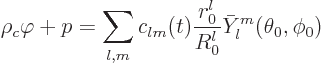

![]()
![]()
![]()
![]()
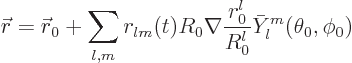
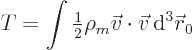
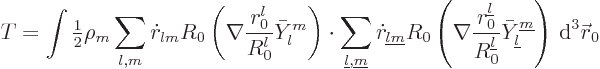
![]()
![]()
![]()
![]()
![]()
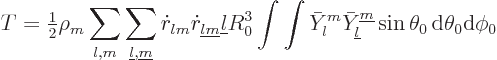
![]()
![]()
![]()
![]()
![]() .
.![]()
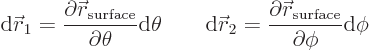
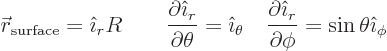

![\begin{eqnarray*}
V_s &=& \sigma \int\int R_0^2 \sin\theta{ \rm d}\theta{\rm d...
...i}\right)^2
\right]
R_0^2 \sin\theta{ \rm d}\theta{\rm d}\phi
\end{eqnarray*}](img5605.gif)
![]() ,
,![]()
![]()
![]()
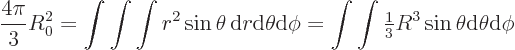
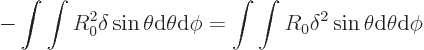
![\begin{eqnarray*}
V_s &=& V_{s,0} - \sigma \int\int \delta^2 \sin\theta{ \rm d...
...i}\right)^2
\right]
R_0^2 \sin\theta{ \rm d}\theta{\rm d}\phi
\end{eqnarray*}](img5611.gif)
![]()

![\begin{displaymath}
I = \int\int
\left[
\frac{\partial \bar Y_l^m}{\partial\t...
...}}{\partial\phi}
\right] \sin\theta{ \rm d}\theta{\rm d}\phi
\end{displaymath}](img5614.gif)
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() .
.![]()
![]() .
.![]()
![]()
![]()
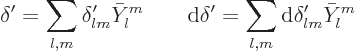
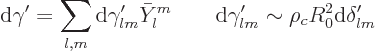
![]()
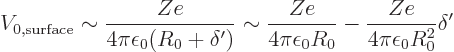
![]()
![]()
![]() .
.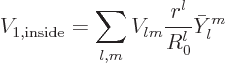
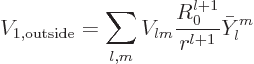
![]() .
.![]() ,
,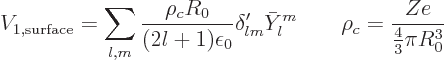
![\begin{displaymath}
{\rm d}V_c =
\left[
\frac{Ze}{4\pi\epsilon_0R_0}
- \frac...
...
\right]
{\rm d}\gamma' \sin\theta{ \rm d}\theta{\rm d}\phi
\end{displaymath}](img5639.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.