| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.77 Impenetrable spherical shell
To solve the problem of particles stuck inside an impenetrable shell
of radius 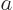 , refer to addendum {A.6}.
According to that addendum, the solutions without unacceptable
singularities at the center are of the form
, refer to addendum {A.6}.
According to that addendum, the solutions without unacceptable
singularities at the center are of the form
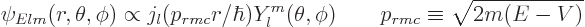 |
(D.53) |
where the 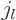 are the spherical Bessel functions of the first kind,
the
are the spherical Bessel functions of the first kind,
the 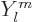 the spherical harmonics, and
the spherical harmonics, and 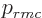 is the classical
momentum of a particle with energy
is the classical
momentum of a particle with energy 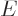 .
. 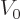 is the constant
potential inside the shell, which can be taken to be zero without
fundamentally changing the solution.
is the constant
potential inside the shell, which can be taken to be zero without
fundamentally changing the solution.
Because the wave function must be zero at the shell 

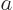 ,
, 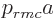

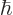 must be one of the zero-crossings of
the spherical Bessel functions. Therefore the allowable energy levels
are
must be one of the zero-crossings of
the spherical Bessel functions. Therefore the allowable energy levels
are
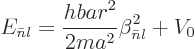 |
(D.54) |
where 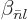 is the
is the 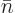 -th zero-crossing of
spherical Bessel function
-th zero-crossing of
spherical Bessel function 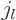 (not counting the origin). Those
crossings can be found tabulated in for example
[1], (under the guise of the Bessel functions of
half-integer order.)
(not counting the origin). Those
crossings can be found tabulated in for example
[1], (under the guise of the Bessel functions of
half-integer order.)
In terms of the count 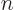 of the energy levels of the harmonic
oscillator,
of the energy levels of the harmonic
oscillator, 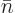
 1 corresponds to energy level
1 corresponds to energy level 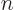

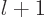 , and each next value of
, and each next value of 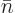 increases the energy
levels by two, so
increases the energy
levels by two, so
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()