D.78 Shell model quadru­pole mo­ment

The re­sult for one pro­ton is read­ily avail­able in lit­er­a­ture and messy to de­rive your­self. If you want to give it a try any­way, one way is the fol­low­ing. Note that in spher­i­cal co­or­di­nates

$$3z^2 - r^2 = 2 r^2 -3 r^2\sin^2\theta$$

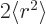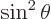and the first term pro­duces $2\langle{r}^2\rangle$ sim­ply by the de­f­i­n­i­tion of ex­pec­ta­tion value. The prob­lem is to get rid of the $\sin^2\theta$ in the sec­ond ex­pec­ta­tion value.

To do so, use chap­ter 12.8, 2. That shows that the sec­ond term is es­sen­tially 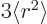$3\langle{r}^2\rangle$ mod­i­fied by fac­tors of the form

$$\langle Y_l^l \vert sin^2\theta Y_l^l\rangle \quad\mbox{and}\quad \langle Y_l^{l-1} \vert sin^2\theta Y_l^{l-1}\rangle$$

where the in­te­gra­tion is over the unit sphere. If you use the rep­re­sen­ta­tion of the spher­i­cal har­mon­ics as given in {D.64}, you can re­late these in­ner prod­ucts to the unit in­ner prod­ucts

$$\langle Y_{l+1}^{l+1} \vert Y_{l+1}^{l+1}\rangle \quad\mbox{and}\quad \langle Y_{l+1}^l \vert Y_{l+1}^l\rangle$$

Have fun.

The ex­pres­sion for the quadru­pole mo­ment if there are an odd num­ber 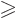$i$ $\raisebox{-.5pt}{$\geqslant$}$ 3 of pro­tons in the shell would seem to be a very messy ex­er­cise. Some text books sug­gest that the odd-par­ti­cle shell model im­plies that the one-pro­ton value ap­plies for any odd num­ber of pro­tons in the shell. How­ever, it is clear from the state with a sin­gle hole that this is un­true. The cited re­sult that the quadru­pole mo­ment varies lin­early with the odd num­ber of pro­tons in the shell comes di­rectly from Krane, [31, p. 129]. No de­riva­tion or ref­er­ence is given. In fact, the re­stric­tion to an odd num­ber of pro­tons is not even stated. If you have a ref­er­ence or a sim­ple de­riva­tion, let me know and I will add it here.