|
|
|
|
|
Next: 14.20 Draft: Gamma Decay |
|
Beta decay is the decay mechanism that affects the largest number of nuclei. It is important in a wide variety of applications, such as betavoltaics and PET imaging.
In standard beta decay, or more specifically, beta-minus decay, a
nucleus converts a neutron into a proton. The number of neutrons ![]()
![]()
Unlike the neutron, the proton has a positive charge, so by itself, converting a neutron into a proton would create charge out of nothing. However, that is not possible as net charge is preserved in nature. In beta decay, the nucleus also emits a negatively charged electron, making the net charge that is created zero as it should.
But there is another problem with that. Now a neutron with spin
![]()
![]() .
.![]() ,
,
Nowadays the neutrino emitted in beta decay is more accurately identified as the electron antineutrino. An antineutrino is the antiparticle of an ordinary neutrino, just like the positron is the antiparticle of the electron. (Particles and antiparticles are exact opposites in all properties except mass, but including charge, allowing a particle and the corresponding antiparticle to annihilate each other, leaving only photons.)
The reason that an antineutrino is emitted rather than a neutrino is
known as conservation of lepton number.
Leptons are
elementary particles that do not respond to the “strong
force,” including electrons and neutrinos. The net lepton
number is defined as the number of leptons, minus the number of
antileptons. It is found that this number is conserved in nature. So
when in beta decay the nucleus emits an electron, a lepton, and an
antineutrino, an antilepton, the lepton number stays unchanged as it
should (like net angular momentum and net charge stay unchanged, as
already noted).
The antineutrino does not affect the basics of beta decay, as it has no charge and virtually zero mass. However, the antineutrino does affect the detailed analysis; for one, the antineutrino can come out with a lot of kinetic energy, thus reducing the otherwise expected kinetic energy of the electron.
In beta decay, the new nucleus must be lighter than the original one.
Classical mass conservation would say that the reduction in nuclear
mass must equal the mass of the emitted electron plus the (negligible)
mass of the antineutrino. However, Einstein’s mass-energy
relation implies that that is not quite right. Mass is equivalent to
energy, and the rest mass reduction of the nucleus must also provide
the kinetic energies of the electron and neutrino, as well as the
(much smaller) one that the nucleus itself picks up during the decay
by recoil
.
Still, the bottom line is that the nuclear mass reduction must be at least the rest mass of the electron (plus antineutrino). In energy units, it must be at least 0.511 MeV, the rest mass energy of the electron. The first subsection below will graphically examine which nuclei have enough energy to beta decay.
Beta-plus decay is the opposite of beta decay. In beta-plus decay, the nucleus converts a neutron into a proton instead of the other way around. To conserve charge, the nucleus can emit a positron, and with it, an electron neutrino to conserve angular momentum and lepton number.
However, while converting a proton into a neutron, the nucleus has a
much easier way to conserve charge. Instead of emitting a positively
charged positron, it can absorb a negatively charged electron from the
atom it is in. The electron's charge then cancels that of the proton.
To preserve angular momentum and lepton number, an electron neutrino
is again emitted. This process is called “electron
capture” (or also K-capture
or
L-Capture
depending on the electron shell name from
which the electron is swiped). Now the nuclear mass reduction does
not need to provide the 0.512 MeV rest mass energy of a positron.
Instead the nuclear mass can increase up to the 0.512 MeV rest mass
energy of the electron that disappears.
So electron capture can occur in circumstances where positron creation is not possible. However, if the nuclear mass reduction is plenty for both electron capture and positron emission, the latter tends to dominate. The reason is the large quantum mechanical uncertainty in position of the low-energy atomic electron. This uncertainty dwarfs the size of the nucleus. It makes it very unlikely for the electron to be found inside the nucleus. A high-energy positron created by the nucleus itself can be created in any state, including high energy ones with short wave lengths.
Also note electron capture is of course not possible if somehow the nucleus has been stripped of all its atomic electrons, like might occur in space.
Electron capture is also called inverse beta decay,
because an electron being absorbed by a nucleus is much like a movie
of an electron being emitted played backwards in time. But there are
some problems with this idea. For one, the time-reversed movie would
also have an electron antineutrino going into the nucleus, not an
electron neutrino coming out.
Still, absorption of a particle is much like the emission of the corresponding antiparticle, at least as far as conservation laws other than energy are concerned. For example, capture of an electron adds one unit of negative charge, while emission of a positron removes one unit of positive charge. Either way, the nuclear charge becomes one unit more negative. In those terms, the notion of “inverse beta decay” may not be that far out, especially since the neutrino is a minor actor in the first place.
As the introduction explained, in beta decay a nucleus converts a neutron into a proton, thus changing into a different nucleus. It can only occur if the nuclear mass reduction exceeds the 0.511 MeV rest mass energy of the electron emitted in the process.
Figures 14.47 through 14.50 show the nuclear mass reduction for beta decay as the vertical coordinate. The reduction exceeds the rest mass energy of the electron only above the horizontal center bands. The left half of each square indicates the nucleus before beta decay, the right half the one after the decay. The horizontal coordinate indicates the atomic numbers, with the values and element symbols as indicated. Neutron numbers are listed at the square itself. Lines connect pairs of nuclei with equal neutron excess.
If the left-half square is colored blue, beta decay is observed. Blue left-half squares are only found above the center bands, so the mass reduction is indeed at least the mass of the electron. However, some blue left-half squares are right on top of the band. Their beta decay should be very slow.
Note that some left-half squares above the band may not be blue. The color indicates the dominant decay process, so if the left-hand nucleus also experiences another decay mode in addition to beta decay, like alpha decay or beta-plus decay with another nucleus, and at a higher rate, its half square will not be blue. However, there should be no left-half squares above the band that are stable green.
Note here that even-even nuclei ![]()
![]()
forbidden
in the sense
discussed in section 14.19.6.
In beta-plus decay, the nucleus converts a proton into a neutron instead of the other way around. To find the energy release in that process, the figures may be read the other way around. The nucleus before the decay is now the right hand one, and the decay is observed when the right-half square is red.
The energy release is now positive downward, and it is now below the center bands that the nuclear mass reduction is sufficient to produce the rest mass of a positron that can carry the proton’ positive charge away. The positron, the anti-particle of the electron, has the same mass as the electron but opposite charge.
But note that red right-half squares extend to within the center bands. The reason is that instead of emitting a positron, the nucleus can capture an electron from the atomic electron cloud surrounding the nucleus. In that case, rather than having to come up with an electron mass worth of energy, the nucleus receives an infusion of that amount of energy. So the required energy goes down by two electron masses.
It follows that the left-hand nucleus will suffer beta decay if the square is above the top of the band, while the right-hand nucleus will suffer electron capture if the square is below the top of the band. Therefore at most one nucleus of each pair can be stable.
Note, once more, that color indicates the dominant decay mode. So
right-half squares below the top of the band do not have to be red;
they just should not be stable green. This is especially relevant for
the odd-odd nuclei in figures 14.49 and
14.50. Odd-odd nuclei are unusually unstable, and the
even-even nuclei they decay into are unusually stable. So it is quite
likely that an odd-odd nuclei in the region of relatively stable
nuclei finds that it has enough energy to both beta decay to the
neighboring even-even nucleus of higher ![]()
![]() .
.
One example is ![]()
The magic neutron numbers are quite visible in figures 14.47 through 14.50. For example, diagonal bands at neutron numbers 50, 82, and 126 are prominent in all four figures. Consider for example figure 14.48. For the 50/49 neutron nuclei, beta decay takes the tightly bound 50th neutron to turn into a proton. That requires relatively large energy, so the energy release is reduced. For the neighboring 52/51 nuclei, beta decay takes the much less tightly bound 52nd neutron, and the energy release is correspondingly higher.
The magic proton numbers tend to show up as step-downs in the curves.
For example, consider the nuclei at the vertical ![]()
![]()
When the neutron and proton magic number lines intersect, combined effects can be seen. One pointed out by Mayer in her Noble prize acceptance lecture [[10]] is the decay of argon-39. It has 18 protons and 21 neutrons. If you interpolate between the neighboring pairs of nuclei on the same neutron excess line in figure 14.47, you would expect argon-39 to be below the top of the center band, hence to be stable against beta decay. But the actual energy release for argon-39 is unusually high, and beta decay it does. Why is it unusually high? For the previous pairs of nuclei, beta decay converts a neutron in the neutron shell that ends at magic number 20 into a proton in the corresponding proton shell. For the suvsequent pairs, beta decay converts a neutron in the neutron shell that ends at magic number 28 to a proton in the corresponding proton shell. Only for argon-39, beta decay converts a neutron in the neutron shell that end at magic number 28 into a proton in the lower energy proton shell that ends at magic number 20. The lowering of the major shell releases additional energy, and the decay has enough energy to proceed.
In figures 14.47 and 14.48, the lowest line
for the lightest nuclei is unusually smooth. These lines correspond
to a neutron excess of 1 or ![]() 1
1
These lines also show that beta-plus decay and electron capture become energetically favored when the nuclei get heavier. That is to be expected since this are nuclei with almost no neutron excess. For the heavier ones, it is therefore energetically favorable to convert protons into neutrons, rather than the other way around.
Since the von Weizsäcker formula of section 14.10.2 predicts nuclear mass, it can be used to predict whether beta-minus or beta-plus/electron capture will occur.
The mathematics is relatively simple, because the mass number ![]()
![]() .
.![]()
![]() .
.![]()
It is then seen that beta-minus decay, respectively beta-plus
decay / electron capture occurs for a pair of nuclei depending whether
the average ![]()
The result is plotted as the black curve in the decay graph figure 14.51. It gives the location where the change in nuclear mass is just enough for either beta-minus decay or electron capture to occur, with nothing to spare. The curve locates the stable nuclei fairly well. For light nuclei, the curve is about vertical, indicating there are equal numbers of protons and neutrons in stable nuclei. For heavier nuclei, there are more neutrons than protons, causing the curve to deviate to the right, the direction of increasing neutron excess.
Because of the pairing energy, stable even-even nuclei can be found well away from the curve. Conversely, stable odd-odd nuclei are hard to find at all. In fact, there are only four: hydrogen-2 (deuterium), lithium-6, boron-10, and nitrogen-14. For comparison, there are 150 stable even-even ones. For nuclei of odd mass number, it does not make much difference whether the number of protons is odd or the number of neutrons: there are 49 stable odd-even nuclei and 53 stable even-odd ones.
(There is also the bizarre excited
![]()
![]()
As an example of the instability of odd-odd nuclei, consider the
curious case of potassium-40, ![]() .
.
But decay it does. Despite the two billion year average lifetime, there are so many potassium-40 nuclei in a human body that almost 5 000 decay per second anyway. About 90% do so through beta decay and end up as the doubly-magic calcium-40. The other 10% decay by electron capture or positron emission and end up as even-even argon-40, with 18 protons and 22 neutrons. So potassium-40 suffers all three beta decay modes, the only relatively common nucleus in nature that does.
Admittedly only 0.001% decays through positron emission. The nuclear mass difference of 0.99 MeV with argon-40 is enough to create a positron, but not by much. Before a positron can be created, potassium is almost sure to have captured an electron already. For a nucleus like xenon-119 the mass difference with iodine-119 is substantially larger, 4.5 MeV, and about 4 in 5 xenon-119 nuclei decay by positron emission, and the fifth by electron capture.
It is energetically possible for the potassium-40 decay product
calcium-40 to decay further into argon-40, by capturing two electrons
from the atom. Energetically possible means that this does not
require addition of energy, it liberates energy, so it can occur
spontaneously. Note that calcium-40 would have to capture two
electrons at the same time; capturing just one electron would turn it
into potassium-40, and that requires external energy addition. In
other words, calcium-40 would have to skip over the intermediate
odd-odd potassium 40. While it is possible, it is believed that
calcium-40 is stable; if it decays at all, its half-life must be more
than 5.9 zettayear (5.9 1![]()
But some even-even nuclei do decay through “double beta-minus” decay. For example, germanium-76 with 32 protons and 44 neutrons will in a couple of zettayear emit two electrons and so turn into even-even selenium-76, skipping over odd-odd arsenic-76 in the process. However, since the entire lifetime of the universe is much less than the blink of an eye compared to a zettayear, this does not get rid of much germanium-76. About 7.5% of natural germanium is germanium-76.
The reduced stability of odd-odd nuclei is the main reason that technetium (Tc) and promethium (Pm) can end up with no stable isotopes at all while their immediate neighbors have many. Both technetium and promethium have an odd-odd isotope sitting right on top of the separating line between beta-minus and beta-plus decay; technetium-98 respectively promethium-146. Because of the approximation errors in the von Weizsäcker formula, they are not quite on the theoretical curve in figure 14.51. However, examination of the experimental nuclear masses shows the excess mass reduction for beta-minus decay and electron capture to be virtually identical for these odd-odd nuclei. And in fact promethium-146 does indeed decay both ways. Technetium-98 could too, but does not; it finds it quicker to create an electron than to capture one from the surrounding atom.
Because the theoretical stable line slopes towards the right in figure 14.51, only one of the two odd-even isotopes next to technetium-98 should be unstable, and the same for the ones next to promethium-146. However, the energy liberated in the decay of these odd-even nuclei is only a few hundred keV in each case, far below the level for which the von Weizsäcker formula is anywhere meaningful. For technetium and promethium, neither neighboring isotope is stable. This is a qualitative failure of the von Weizsäcker model. But it is rare; it happens only for these two out of the lowest 82 elements. Few books even mention it is a fundamental failure of the formula.
The kinetic energy of nuclear decay products is important to understand the correct nature of the decay.
Historically, one puzzling observation in beta decay was the kinetic energies with which the electrons came out. When the beta decay of a collection of nuclei of a given type is observed, the electrons come out with a range of kinetic energies. In contrast, in the alpha decay of a collection of nuclei of a given type, all alpha particles come out with pretty much the exact same kinetic energy.
Consider the reason. The total kinetic energy release in the decay of
a given nucleus is called the
Following
Einstein’s famous relation ![]()
![]()
![]()
![]() ,
,![]()
Since energy must be conserved, the reduction in rest mass energy
given by the ![]() -
-
Now, excluding the special case of beryllium-8, the mass of the alpha
particle is much smaller than that of the final nucleus. So the
expression above shows that the kinetic energy of the final nucleus is
much less than that of the alpha particle. The alpha particle runs
away with almost all the kinetic energy. Its kinetic energy is almost
equal to ![]() .
.![]() .
.
In beta decay, things would be pretty much the same if just an
electron was emitted. The electron too would come out with a single
kinetic energy. The fact that it did not led Pauli to propose that
another small particle also comes out. That particle could carry away
the rest of the kinetic energy. It had to be electrically neutral
like a neutron, because the nuclear charge change is already accounted
for by the charge taken away by the electron. The small neutral
particle was called the neutrino
by Fermi. The
neutrino was also required for angular momentum conservation: a proton
and an electron each with spin ![]()
![]()
The neutrino that comes out in beta-minus decay is more accurately
called an electron antineutrino and usually indicated by
![]() .
.
The analysis of the kinetic energy of the decay products changes
because of the presence of an additional particle. The
![]() -
-
As an aside, it should be noted that the nuclear masses in the ![]()
![]() -
-
It should also be noted that if the initial and/or final nucleus is in
an excited state, its mass can be computed from that of the ground
state nucleus by adding the excitation energy, converted to mass units
using ![]()
![]()
![]() .
.
Because the amount of kinetic energy that the neutrino takes away
varies, so does the kinetic energy of the electron. One extreme case
is that the neutrino comes out at rest. In that case, the given
analysis for alpha decay applies pretty much the same way for beta
decay if the alpha is replaced by the electron. This gives the
maximum kinetic energy at which the electron can come out to be
![]() .
.![]() .
.
A further modification to the analysis for the alpha particle must be made. Because of the relatively small masses of the electron and neutrino, they come out moving at speeds close to the speed of light. Therefore the relativistic expressions for momentum and kinetic energy must be used, chapter 1.1.2.
Consider first the extreme case that the electron comes out at rest.
The relativistic energy expression gives for the kinetic energy of the
neutrino:
| (14.53) |
The small fraction of the kinetic energy that does end up with the
nucleus may now be estimated, because the nucleus has the same
magnitude of momentum ![]() .
.
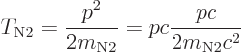 |
(14.54) |
The extreme case that the neutrino is at rest can be computed in much
the same way, except that the rest mass energy of the electron is
comparable to ![]()
![]() .
.![]()
![\begin{displaymath}
pc = \sqrt{
\frac{[E^2 - (E_{\rm N2}+E_{\rm e})^2]
[E^2 -...
...}-E_{\rm e})^2]}{4E^2}}
\qquad E = E_{\rm N2} + E_{\rm e} + Q
\end{displaymath}](img3453.gif) |
(14.55) |
In the case of beta-plus decay, the electron becomes a positron and
the electron antineutrino becomes an electron neutrino. However,
antiparticles have the same mass as the normal particle, so there is
no change in the energetics. (There is a difference if it is written
in terms of atomic instead of nuclear masses.) In case of electron
capture, it must be taken into account that the nucleus receives an
infusion of mass equal to that of the captured electron. The
![]() -
-
The binding energy may be ballparked from the hydrogen ground state
energy, chapter 4.3, by simply replacing ![]()
![]() .
.
| (14.58) |
Energetics is not all there is to beta decay. Some decays are
energetically fine but occur extremely slowly or not at all. Consider
calcium-48 in figure fig:betdec2e. The square is well above the
center band, so energy-wise there is no problem at all for the decay
to scandium-48. But it just does not happen. The half life of
calcium-48 is 64 1![]()
The big problem is angular momentum conservation. As an even-even nucleus, calcium-48 has zero spin, while scandium-48 has spin 6 in its ground state. To conserve angular momentum during the decay, the electron and the antineutrino must therefore take six units of spin along. But to the extend that the nuclear size can be ignored, the electron and antineutrino come out of a mathematical point. That means that they come out with zero orbital angular momentum. They have half a unit of spin each, and there is no way to produce six units of net spin from that. The decay is forbidden by angular momentum conservation.
Of course, calcium-48 could decay to an excited state of scandium-48. Unfortunately, only the lowest two excited states are energetically possible, and these have spins 5 and 4. They too are forbidden.
To understand what beta decays are forbidden, the first step is to examine what decays are allowed.
Consider the spins of the electron and antineutrino. They could combine into a net spin of zero. If they do, it is called a “Fermi decay.” Since the electron and antineutrino take no spin away, in Fermi decays the nuclear spin cannot change.
The only other possibility allowed by quantum mechanics is that the
spins of electron and antineutrino combine into a net spin of one;
that is called a “Gamow-Teller decay.” The rules of quantum mechanics for the
addition of angular momentum vectors imply:
Putting it together, the angular momentum can change by up to one unit
in an allowed beta decay. Also, if there is no orbital angular
momentum, the parities of the electron and antineutrino are even, so
the nuclear parity cannot change. In short
One simple example of an allowed decay is that of a single neutron
into a proton. Since this is a ![]()
![]()
Some disclaimers are in order. Both the discussion above and the following one for forbidden decays are nonrelativistic. But neutrinos are very light particles that travel at very close to the speed of light. For such relativistic particles, orbital angular momentum and spin get mixed-up. That is much like they get mixed-up for the photon. That was such a headache in describing electromagnetic transitions in chapter 7.4.3. Fortunately, neutrinos turn out to have some mass. So the given arguments apply at least under some conditions, even if such conditions are never observed.
A much bigger problem is that neutrinos and antineutrinos do not
conserve parity. That is discussed in more detail a later subsection,
Above, this book simply told you a blatant lie when it said that the
electron-antineutrino system, (or the positron-neutrino system in
beta-plus decay), comes off with zero parity. A system involving a
single neutrino or antineutrino does not have definite parity. And
parity is not conserved in the decay process anyway. But the initial
and final nuclear states do have definite parity (to within very high
accuracy). Fortunately, it turns out that you get the right answers
for the change in nuclear parity if you simply assume that the
electron and antineutrino come off with the parity given by their
orbital
angular momentum.
No you cannot have your money back. You did not pay any.
A relativistic description of neutrinos can be found in {A.44}.
As noted at the start of this subsection, beta decay of calcium-48 requires a spin change of at least 4 and that is solidly forbidden. But forbidden is not quite the same as impossible. There is a small loophole. A nucleus is not really a mathematical point, it has a nonzero size.
Classically that would not make a difference, because the orbital
angular momentum would be much too small to make up the deficit in
spin. A rough ballpark of the angular momentum of, say, the electron
would be ![]() ,
,![]()
![]()
![]() .
.
But quantum mechanics says that the orbital momentum cannot be
a small fraction of ![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
In particular, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Decays with ![]()
![]()
![]()
That will not do for calcium-48, because at least 4 units of spin
change is needed. In second-forbidden decays,
the
electron and neutrino come out with a net orbital angular momentum
![]()
![]()
In third forbidden decays, ![]()
![]()
Beta decay of calcium-48 is possible through fourth-forbidden
transitions:
There is an additional effect slowing down the beta decay of the ![]()
![]()
![]() -
-
One reason that is bad news, (or good news, if you like calcium-48),
is because it makes the momentum of the electron and neutrino
correspondingly small. The ratio ![]()
![]()
![]()
![]() ;
;![]()
![]()
![]()
![]()
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,28...
...beta^-$}}
\put(-50,92){\makebox(0,0)[l]{$\beta^+$}}
\end{picture}
\end{figure}](img3478.gif) |
There is another, smaller, effect. Even if the final nucleus is the
![]()
![]() -
-![]()
![]()
The Fermi integral shows beta plus decay is additionally slowed down,
because it is more difficult to create a positron at a strongly
repelling positively charged nucleus. The relativistic Fermi integral
also depends on the nuclear radius, hence a bit on the mass number.
Figure 14.52 used a ballpark value of the mass number for
each ![]()
The Fermi integral applies to allowed decays, but the general idea is
the same for forbidden decays. In fact, half-lives ![]()
![]()
![]() -
-![]() -
-
You see how calcium-48 can resist beta-decay for 64 1![]()
![]()
Figure 14.53 shows nuclei that decay primarily through beta-minus decay in blue. Nuclei that decay primarily through electron capture and beta-plus decay are shown in red. The sizes of the squares indicate the decay rates. For reference, the stable and double-beta decay nuclei are shown as full-size green squares.
Note the tremendous range of decay rates. It corresponds to
half-lives ranging from milliseconds to 1![]()
The decay rates in figure 14.53 are color coded according to a guesstimated value for how forbidden the decay is. Darker red or blue indicate more forbidden decays. Note that more forbidden decays tend to have much lower decay rates. (Lightly colored squares indicate nuclei for which the degree to which the decay is forbidden could not be guesstimated by the automated procedures used.)
Figure 14.54 shows the decay rates normalized with a
theoretical guesstimate for them. Note the greatly reduced range of
variation that the guesstimate achieves, crude as it may be. One
major success story is for forbidden decays. These are often so slow
that they must be shown as minimum-size dots in figure
14.53 to be visible. However, in figure 14.54
they join the allowed decays as full-size squares. Consider in
particular the three slowest decays among the data set. The slowest
of all is vanadium-50, with a half-life of 150 1![]()
![]()
![]()
unstable
isotope indium-115.
Their dots in figure 14.53 become full squares in figure
14.54.
Another eye-catching success story is
![]() ,
,![]() ,
,![]() -
-
The ballparks were obtained from the Fermi theory
of
beta decay, as discussed in detail in addendum {A.45}.
Unlike the relatively simple theory of alpha decay, the Fermi theory
is elaborate even in a crude form. Taking beta-minus decay as an
example, the Fermi theory assumes a pointwise interaction between
the wave functions of the neutron that turns into a proton and those
of the electron/antineutrino pair produced by the decay. (Quantum
mechanics allows the neutron before the decay to interact with the
electron and neutrino that would exist if it had already decayed.
That is a twilight
effect, as discussed in chapter
5.3 and more specifically in addendum
{A.24} for gamma decay.) The strength of the
interaction is given by empirical constants.
Note that for many nuclei no ballparks were found. One major reason
is that the primary decay mechanism is not necessarily to the ground
state of the final nucleus. If decay to the ground state is
forbidden, decay to a less-forbidden excited state may dominate.
Therefore, to correctly estimate the decay rate for a given nucleus
requires detailed knowledge about the excited energy states of the
final nucleus. The energies of these excited states must be
sufficiently accurately known, and they may not be. In particular,
for a few nuclei, the energy release of the decay, or ![]() -
-![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.![]() -
-![]() -
-![]() -
-
In addition to the energy of the excited states, their spins and parities must also be accurately known. The reason is that they determine to what level the decay is forbidden, hence slowed down. The computer program that produced figures 14.53 and 14.54 assumed conservatively that if no unique value for spin and/or parity was given, it might be anything. Also, while there was obviously no way for the program to account for any excited states whose existence is not known, the program did allow for the possibility that there might be additional excited states above the highest energy level known. This is especially important well away from the stable line where the excited data are often sparse or missing altogether. All together, for about one third of the nuclei processed, the uncertainty in the ballparked decay rate was judged too large to be accepted. For the remaining nuclei, the level to which the decay was forbidden was taken from the excited state that gave the largest contribution to the decay rate.
The Fermi ballparks were constructed such that the true decay rate
should not be significantly more than the ballparked one. In general
they met that requirement, although for about 1% of the nuclei, the
true decay rate was more ten times the ballparked ones, reaching up to
370 times for ![]() .
.![]() -
-![]() -
-
Note that while the true decay rate should not be much more than the
ballparked one, it is very possible for it to be much less. The
ballpark does not consider the details of the nuclear wave function,
because that is in general prohibitively difficult. The ballpark
simply hopes that if a decay is not strictly forbidden by spin or
parity at level ![]() ,
,
As an example, compare the decay processes of scandium-41 and
calcium-47. Scandium-41, with 21 protons and 20 neutrons, decays into
its mirror twin calcium-41, with 20 protons and 21 neutrons. The
decay is almost all due to beta-plus decay to the ground state of
calcium-41. According to the shell model, the lone proton in the
4![]()
![]()
![]() .
.
All the electron capture / beta-plus decays of the nuclei immediately
to the left of the vertical ![]()
![]()
![]()
But now consider the beta-minus decay process of calcium-47 to
scandium-47. Calcium-47 has no protons in the 4![]()
![]()
hole
in the
4![]()
![]()
At least one source claims that in the odd-particle shell model “all odd particles
are treated equivalently,” so that we might expect that the
calcium-47 decay is superallowed just like the scandium-41 one.
That is of course not true. The odd-particle shell model does
emphatically not treat all odd particles equivalently. It only says
that, effectively, an even number of nucleons in the shell pair up
into a state of zero net spin, leaving the odd particle to provide the
net spin and electromagnetic moments. That does not mean that the
seventh 4![]()
As another example, consider the beta-plus decay of oxygen-14 to
nitrogen-14. Their isobaric analog states were identified in figure
14.46. Decay to the ground state is allowed by spin and
parity, at a ballparked decay rate of 0.23/s. However, the true decay
proceeds at a rate 0.01/s, which just happens to be 1.6 times the
ballparked decay rate to the ![]()
![]() -
-
Superallowed decays like the one of oxygen-14 to the corresponding
isobaric analog state of nitrogen-14 are particularly interesting
because they are ![]()
![]()
The horror story of a poor match up between the nuclear wave function
produced by the decay Hamiltonian and the final nuclear wave function
is lutetium-176. Lutetium-176 has a ![]()
![]()
![]()
![]()
![]()
The discussed examples show that the Fermi theory does an excellent
job of predicting decay rates if the differences in nuclear wave
functions are taken into account. In fact, if the nuclear wave
function can be accurately accounted for, like in ![]()
![]()
For a long time, physicists believed that the fundamental laws of nature behaved the same when seen in the mirror. The strong nuclear force, electromagnetism, and gravity all do behave the same when seen in the mirror. However, in 1956 Lee and Yang pointed out that the claim had not been tested for the weak force. If it was untrue there, it could explain why what seemed to be a single type of K-meson could decay into end products of different parity. The symmetry of nature under mirroring leads to the law of conservation of parity, chapter 7.3. However, if the weak force is not the same under mirroring, parity can change in weak processes, and therefore, the decay products could have any net parity, not just that of the original K-meson.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(380,12...
...1){\makebox(0,0)[b]{$\fourIdx{60}{27}{}{}{\rm Co}$}}
\end{picture}
\end{figure}](img3492.gif) |
Wu and her coworkers therefore tested parity conservation for the beta decay of cobalt-60 nuclei. These nuclei were cooled down to extremely low temperatures to cut down on their thermal motion. That allowed their spins to be aligned with a magnetic field, as in the left of figure 14.55. It was then observed that the electrons preferentially came out in the direction of motion of a left-handed screw rotating with the nuclear spin. Since a left-handed screw turns into a right-handed one seen in the mirror, it followed that indeed the weak force is not the same seen in the mirror. The physics in the mirror is not the correct physics that is observed.
Since the weak force is weak, this does not affect parity conservation
in other circumstances too much. Formally it means that
eigenfunctions of the Hamiltonian are not eigenfunctions of the parity
operator. However, nuclear wave functions still have a single parity
to very good approximation; the amplitude of the state of opposite
parity mixed in is of the order of 1![]() ,
,
An additional operation can be applied to the mirror image in
14.55 to turn it back into a physically correct decay.
All particles can be replaced by their antiparticles. This
operation is called “charge conjugation,” because among other things it changes the
sign of the charge for each charged particle. In physics, you are
always lucky if a name gets some of it right. Some of the particles
involved may actually be charged, and conjugation
is a
sophisticated-sounding term to some people. It is also a
vague term that quite conceivably could be taken to mean
reversal of sign
by people naive enough to consider
conjugation
sophisticated. Charge conjugation turns
the electrons going around in the loops of the electromagnet in
figure 14.55 into positrons, so the current reverses
direction. That must reverse the sign of the magnetic field if the
physics is right. But so will the magnetic moment of anticobalt-60
nucleus change sign, so it stays aligned with the magnetic field. And
physicist believe the positrons will preferentially come out of
anticobalt-60 nuclei along the motion of a right-handed screw.
Besides this combined charge conjugation plus parity (CP) symmetry of nature, time symmetry is also of interest here. Physical processes should remain physically correct when run backwards in time, the same way you can run a movie backwards. It turns out that time symmetry too is not completely absolute, and neither is CP symmetry for that matter. However, if all three operations, charge conjugation (C), mirroring (P), and time inversion (T), together are applied to a physical process, the resulting process is believed to always be physically correct. There is a theorem, the CPT theorem, that says so under relatively mild assumptions.