|
|
|
|
|
Next: 1.2 The Lorentz Transformation |
|
Special relativity is commonly attributed to Albert Einstein’s 1905 papers. That is certainly justifiable. However, Einstein swiped the big ideas of relativity from Henri Poincaré, (who developed and named the principle of relativity in 1895 and a mass-energy relation in 1900), without giving him any credit or even mentioning his name.
He may also have swiped the underlying mathematics he used from Lorentz, (who is mentioned, but not in connection with the Lorentz transformation.) However, in case of Lorentz, it is possible to believe that Einstein was unaware of his earlier work, if you are so trusting. Before you do, it must be pointed out that a review of Lorentz’ 1904 work appeared in the second half of February 1905 in Beiblätter zu den Annalen der Physik. Einstein was well aware of that journal, since he wrote 21 reviews for it himself in 1905. Several of these were in the very next issue after the one with the Lorentz review, in the first half of March. Einstein’s first paper on relativity was received June 30 1905 and published September 26 in Annalen der Physik. Einstein had been regularly writing papers for Annalen der Physik since 1901. You do the math.
In case of Poincaré, it is known that Einstein and a friend pored
over Poincaré’s 1902 book “Science and
Hypothesis.” In fact the friend noted that it kept them
breathless for weeks on end.
So Einstein cannot
possibly have been unaware of Poincaré’s work.
However, Einstein should not just be blamed for his boldness in swiping most of the ideas in his paper from then more famous authors, but also be commended for his boldness in completely abandoning the basic premises of Newtonian mechanics, where earlier authors wavered.
It should also be noted that general relativity can surely be credited to Einstein fair and square. But he was a lot less hungry then. And had a lot more false starts. (There is a possibility that the mathematician Hilbert may have some partial claim on completing general relativity, but it is clearly Einstein who developed it. In fact, Hilbert wrote in one paper that his differential equations seemed to agree with the “magnificent theory of general relativity established by Einstein in his later papers.” Clearly then, Hilbert himself agreed that Einstein established general relativity.)
The most important result of relativity for the rest of this book is
without doubt Einstein’s famous relation ![]()
![]()
![]() .
.![]()
![]()
![]()
The relation implies that the kinetic energy of a particle is not
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
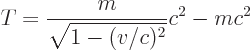
For velocities small compared to the tremendous speed of light, this
is equivalent to the classical ![]() .
.
The photons of electromagnetic radiation, (which includes radio waves,
microwaves, light, x-rays, gamma rays, etcetera), do travel at the
speed of light through a vacuum. However, the only reason that they
can do so is because they have zero rest mass ![]() .
.
If the kinetic energy is the difference between ![]()
![]() ,
,rest mass energy
![]()
Quantum mechanics does not use the speed ![]()
![]()
![]()
![]() .
.
The key discovery of relativity is that the observed speed of light
through vacuum is the same regardless of how fast you are traveling.
One historical step that led to this discovery was a famous experiment
by Michelson & Morley. In simplified terms, Michelson & Morley
tried to determine the absolute speed of the earth through space by
horse-racing
it against light. If a passenger jet
airplane flies at three quarters of the speed of sound, then sound
waves going in the same direction as the plane only have a speed
advantage of one quarter of the speed of sound over the plane. Seen
from inside the plane, that sound seems to move away from it at only a
quarter of the normal speed of sound.
Essentially, Michelson & Morley reasoned that the speed of the earth could similarly be observed by measuring how much it reduces the apparent speed of light moving in the same direction through a vacuum. But it proved that the motion of the earth produced no reduction in the apparent speed of light whatsoever. It is as if you are racing a fast horse, but regardless of how fast you are going, you do not reduce the velocity difference any more than if you would just stop your horse and have a drink.
The simplest explanation would be that earth is at rest compared to the universe. But that cannot possibly be true. Earth is a minor planet in an outer arm of the galaxy. And earth moves around the sun once a year. Obviously, the entire universe could not possibly follow that noninertial motion.
So how come that earth still seems to be at rest compared to light waves moving through vacuum? You can think up a hundred excuses. In particular, the sound inside a plane does not seem to move any slower in the direction of motion. But of course, sound is transmitted by real air molecules that can be trapped inside a plane by well established mechanisms. It is not transmitted through empty space like light.
But then, at the time of the Michelson & Morley experiment the
prevailing theory was that light did move through some
hypothetical medium. This made-up medium was called the
ether.
It was supposedly maybe dragged along by the
earth, or maybe dragged along a bit, or maybe not after all. In fact,
Michelson & Morley were really trying to decide how much it was being
dragged along. Looking back, it seems self-evident that this ether
was an unsubstantiated theory full of holes. But at the time most
scientists took it very seriously.
The results of the Michelson & Morley experiment and others upped the
ante. To what could reasonably be taken to be experimental error, the
earth did not seem to move relative to light waves in vacuum. So in
1895 Poincaré reasoned that experiments like the one of Michelson &
Morley suggested that it is impossible to detect absolute motion. In
1900 he proposed the Principle of Relative Motion.
It
proposed that the laws of movement would be the same in all coordinate
systems regardless of their velocity, as long as they are not
accelerating. In 1902, in the book read by Einstein, he discussed
philosophical assessments on the relativity of space, time, and
simultaneity, and the idea that a violation of the relativity
principle can never be detected. In 1904 he called it
“The principle of relativity, according to which the laws of physical phenomena must be the same for a stationary observer as for one carried along in a uniform motion of translation, so that we have no means, and can have none, of determining whether or not we are being carried along in such a motion.”
In short, if two observers are moving at different, but constant speeds, it is impossible to say which one, if any, is at rest. The laws of physics observed by the two observers are exactly the same. In particular, the
moving observers see the same speed of light regardless of their different physical motion.
(Do note however that if an observer is accelerating or spinning around, that can be determined through the generated inertia forces. Not all motion is relative. Just an important subset of it.)
A couple of additional historical notes may be appropriate. Quite a
number of historians of science argue that Poincaré did not
really
propose relativity, because he continued to use
the ether in various computations afterwards. This argument is
unjustified. To this very day, the overwhelming majority of
physicists and engineers still use Newtonian physics in their
computations. That does not mean that these physicists and engineers
do not believe in special relativity. It means that they find doing
the Newtonian computation a lot easier, and it gives the right answer
for their applications. Similarly, Poincaré himself clearly stated
that he still considered the ether a “convenient
hypothesis.” There were well established procedures for
computing such things as the propagation of light in moving media
using an assumed ether that had been well verified by experiment.
A more interesting hypothesis advanced by historians is that Einstein may have been more inclined to do away with the ether from the start than other physicists. The concept of the ether was without doubt significantly motivated by the propagation of other types of waves like sound waves and water waves. In such waves, there is some material substance that performs a wave motion. Unlike waves, however, particles of all kinds readily propagate through empty space; they do not depend on a separate medium that waves. That did not seem relevant to light, because its wave-like nature had been well established. But in quantum mechanics, the complementary nature of light as particles called photons was emerging. And Einstein may have been more comfortable with the quantum mechanical concept of light than most at the time. He was a major developer of it.
At first, it may not seem such a big deal that the speed of light is the same regardless of the motion of the observer. But when this notion is examined in some more detail, it leads to some very counter-intuitive conclusions.
It turns out that if observers are in motion compared to each other, they will unavoidably disagree about such things as spatial distances and the time that things take. Often, different observers cannot even agree on which of two physical events takes place earlier than the other. Assuming that they determine the times correctly in their own coordinate system, they will come up with different answers.
Self-evidently, if observers cannot even agree on which of two events happened first, then an absolute time scale that everyone can agree on is not possible either. And neither is a system of absolute spatial coordinates that everybody can agree upon.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(404,41...
...]{Venus}}
\put(185.3,28){\makebox(0,0)[b]{Mars}}
}
\end{picture}
\end{figure}](img32.gif) |
Consider a basic thought experiment. A thought experiment is an experiment that should in principle be possible, but you do not want to be in charge of actually doing it. Suppose that the planets Venus and Mars happen to be at opposite sides of earth, and at roughly the same distance from it. The left side of figure 1.1 shows the basic idea. Experimenters on earth flash simultaneous light waves at each planet. Since Venus happens to be a bit closer than Mars, the light hits Venus first. All very straightforward. Observers on Venus and Mars would agree completely with observers on earth that Venus got hit first. They also agree with earth about how many minutes it took for the light to hit Venus and Mars.
To be sure, the planets move with speeds of the order of 100,000 mph relative to one another. But that speed, while very large in human terms, is so small compared to the tremendous speed of light that it can be ignored. For the purposes of this discussion, it can be assumed that the planets are at rest relative to earth.
Next assume that a space ship with aliens was just passing by and watched the whole thing, like in the right half of figure 1.1. As seen by observers on earth, the aliens are moving to the right with half the speed of light. However, the aliens can argue that it is they that are at rest, and that the three planets are moving towards the left with half the speed of light. According to the principle of relativity, both points of view are equally valid. There is nothing that can show whether the space ship or the planets are at rest, or neither one.
In particular, the speed of the light waves that the aliens observe is identical to the speed that earth sees. But now note that as far as the aliens are concerned, Venus moves with half the speed of light away from its incoming light wave. Of course, that significantly increases the time that the light needs to reach Venus. On the other hand, the aliens see Mars moving at half the speed of light towards its incoming light wave. That roughly halves the time needed for the light wave to hit Mars. In short, unlike earth, the aliens observe that the light hits Mars a lot earlier than it hits Venus.
That example demonstrates that observers in relative motion disagree
about the time difference between events occurring at different
locations. Worse, even if two events happen right in the hands of one
of the observers, the observers will disagree about how long the
entire thing takes. In that case, the observer compared to which the
location of the events is in motion will think that it takes longer.
This is called “time-dilation.” The time difference between two events slows
down according to
An event
can be anything with an unambiguous physical
meaning, like when the hands of a clock reach a certain position. So
clocks are found to run slow when they are in motion compared to the
observer. The best current clocks are accurate enough to directly
measure this effect at human-scale speeds, as low as 20 mph. But
relativity has already been verified in myriad other ways. The time
is long gone that serious scientists still doubted the conclusions of
relativity.
As a more practical example, cosmic rays can create radioactive particles in the upper atmosphere that survive long enough to reach the surface of the earth. The surprising thing is that at rest in a laboratory these same particles would not survive that long by far. The particles created by cosmic rays have extremely high speed when seen by observers standing on earth. That slows down the decay process due to time dilation.
Which of course raises the question: should then not an observer moving along with one such particle observe that the particle does not reach the earth? The answer is no; relativity maintains a single reality; a particle either reaches the earth or not, regardless of who is doing the observing. It is quantum mechanics, not relativity, that does away with a single reality. The observer moving with the particle observes that the particle reaches the earth, not because the particle seems to last longer than usual, but because the distance to travel to the surface of the earth has become much shorter! This is called “Lorentz-Fitzgerald contraction.”
For the observer moving with the particle, it seems that the entire
earth system, including the atmosphere, is in motion with almost the
speed of light. The size of objects in motion seems to contract in
the direction of the motion according to
In short, for the observer standing on earth, the particle reaches
earth because its motion slows down the decay process by a factor
1/![]() .
.
Lorentz-Fitzgerald contraction is also evident in how the aliens see the planets in figure 1.1. But note that the difference in the wave lengths of the light waves is not a simple matter of Lorentz-Fitzgerald contraction. The light waves are in motion compared to both observers, so Lorentz-Fitzgerald contraction simply does not apply.
The correct equation that governs the difference in observed wave
length ![]()
![]() ,
,
In terms of the example figure 1.1, 0 indicates the
emitter earth, and ![]()
![]()
![]()
Doppler shifts.
One related effect is cosmic redshift. The entire universe is expanding. As a result, far away galaxies move away from us at extremely high speeds. That causes wave length shifts; the radiation emitted or absorbed by various excited atoms in these galaxies appears to us to have wave lengths that are too long. The received wave lengths are longer than those that these same atoms would emit or absorb on earth. In particular, the colors of visible light are shifted towards the red side of the spectrum. To observers in the galaxies themselves, however, the colors would look perfectly fine.
Note that the cosmic redshift can only qualitatively be understood from the formulae above. It is more accurate to say that the photons traveling to us from remote galaxies get stretched due to the expansion of the universe. The cosmic redshift is not due to the motion of the galaxies through space, but due to the motion of space itself. If the expansion of space is rephrased in terms of a relative velocity of the galaxies compared to us, that velocity can exceed the speed of light. That would produce nonsense in the formulae above. Objects cannot move faster than the speed of light through space, but the velocity of different regions of space compared to each other can exceed the speed of light.
Returning to the normal Doppler shift, the changes in wave length are not directly due to Lorentz-Fitzgerald contraction. Instead, they can in part be attributed to time dilation. In figure 1.1 both the aliens and earth can deduce the wave length from how frequently the peaks of the wave leave the emitter earth. But in doing so, one source of disagreement is time dilation. Since earth is in motion compared to the aliens, the aliens think that the peaks leave earth less frequently than earth does. In addition, the aliens and earth disagree about the relative velocity between the light waves and earth. Earth thinks that the light waves leave with the speed of light relative to earth. The aliens also think that the light waves travel with the speed of light, but in addition they see earth moving towards the left with half the speed of light. Combine the two effects, for arbitrary velocity of the aliens, and the relation between the wave lengths is as given above. Further, since the speed of light is the same for both earth and aliens, the observed frequency of the light is inversely proportional to the observed wave length.