|
|
|
|
|
Next: IV. Supplementary Information |
|
Nuclear reactions and decays often leave the final nucleus in an quantum state of elevated energy. Such an excited state may lower its energy by emitting a photon of electromagnetic radiation. That is called gamma decay. It is a common way to evolve to the ground state.
Gamma decay is in many respect similar to alpha and beta decay discussed in earlier sections. However, the type of nucleus does not change in gamma decay. Both the atomic and mass number of the nucleus stay the same. (Of course, an excited nuclear state can suffer alpha or beta decay instead of gamma decay. That however is not the subject of this section.)
Gamma decay of excited nuclei is the direct equivalent of the decay of excited electron states in atoms. The big difference between gamma decay and the radiation emitted by the electrons in atoms is energy. The energy of the photons emitted by nuclei is typically even higher than that of the X-ray photons emitted by inner electrons. Therefore the radiation emitted by nuclei is generally referred to as “gamma rays.”
Both atomic radiation and nuclear gamma decay were analyzed in considerable detail in chapter 7.4 through 7.8 and addenda {A.20} through {A.25}. There is no point in repeating all that here. Instead this section will merely summarize the key points and discuss some actual observations.
However, the existing data on gamma decay is enormous. Consider NuDat 2, a standard data base. At the time of writing, it contains over 3 100 nuclei. Almost every nucleus but the deuteron has many excited energy levels; there are over 160 000 in NuDat 2. Gamma decays can proceed between different states, and NuDat 2 contains over 240 000 of them. There is no way that this book can cover all that data. The coverage given in this section will therefore be anecdotal or random rather than comprehensive.
However, based on a simple model, at least ballpark transition rates will be established. These are called the Weisskopf units. They are commonly used as reference values, to give some context to the measured transition rates.
One big limitation of gamma decay is for nuclear states of zero spin. A state of zero spin cannot transition to another state of zero spin by emitting a photon. As discussed in chapter 7.4, this violates conservation of angular momentum.
But there are other ways that a nucleus can get rid of excess energy besides emitting an electromagnetic photon. One way is by kicking an atomic electron out of the surrounding atom. This process is called “internal conversion” because the electron is outside the nucleus. It allows transitions between states of zero spin.
For atoms, two-photon emission is a common way to achieve decays between states of zero angular momentum. However, for nuclei this process is less important because internal conversion usually works so well.
Internal conversion is also important for other transitions. Gamma decay is slow between states that have little difference in energy and/or a big difference in spin. For such decays, internal conversion can provide a faster alternative.
If the excitation energy is high, it is also possible for the nucleus to create an electron and positron pair from scratch. Since the quantum uncertainty in position of the pair is far too large for them to be confined within the small nucleus, this is called “internal pair creation.”
The reduction in nuclear energy during gamma decay is called the
![]() -
-
Recoil energy will usually be ignored, so that ![]()
| (14.65) |
In internal conversion, the nucleus does not emit a photon, but kicks
an electron out of the surrounding atomic electron cloud. The nuclear
energy reduction goes into kinetic energy of the electron, plus the
binding energy required to remove the electron from its orbit:
| (14.66) |
The decay rate in gamma decay is to a large extent dictated by what is allowed by conservation of angular momentum and parity. The nucleus is almost a mathematical point compared to the wave length of a typical photon emitted in gamma decay. Therefore, it is difficult for the nucleus to give the photon additional orbital angular momentum. That is much like what happens in alpha and beta decay.
The photon has one unit of spin. If the nucleus does not give it additional orbital angular momentum, the total angular momentum that the photon carries off is one unit. That means that the nuclear spin cannot change by more than one unit.
(While this is true, the issue is actually somewhat more subtle than in the decay types discussed previously. For a photon, spin and orbital angular momentum are intrinsically linked. Because of that, a photon always has some orbital angular momentum. That was discussed in chapter 7.4.3 and in detail in various addenda such as {A.21}. However, the inherent orbital angular momentum does not really change the story. The bottom line remains that it is unlikely for the photon to be emitted with more than one unit of net angular momentum.)
The nuclear spin can also stay the same, instead of change by one unit, even if a photon with one unit of angular momentum is emitted, In classical terms the one unit of angular momentum can go into changing the direction of the nuclear spin instead of its magnitude, chapter 7.4.2. However, this only works if the nuclear spin is nonzero.
Parity must also be preserved, chapter 7.4. Parity is
even, or 1, if the wave function stays the same when the positive
direction of all three Cartesian axes is reversed. Parity is odd, or
![]() 1
1
In the normal, or allowed,
decays the photon is
emitted with odd parity. Therefore, the nuclear parity must reverse
during the transition, chapter 7.4.2.
(To be picky, the so-called weak force does not preserve parity. This creates a very small uncertainty in nuclear parities. That then allows a very small probability for transitions in which the apparent parity is not conserved. But the probability for this is so small that it can almost always be ignored.)
Allowed transitions are called electric transitions because the nucleus interacts mainly with the electric field of the photon. More specifically, they are called “electric dipole transitions” for reasons originating in classical electromagnetics, chapter 7.7.2. For practical purposes, a dipole transition is one in which the photon is emitted with one unit of net angular momentum.
Transitions in which the nuclear spin change is greater than one unit,
or in which the nuclear parity does not change, or in which the spin
stays zero, are called forbidden.
Despite the name,
most such decays will usually occur given enough time. However they
are generally much slower.
One way that forbidden transitions can occur is that the nucleus interacts with the magnetic field instead of the electric field. This produces what are called magnetic transitions. Magnetic transitions tend to be noticeably slower than corresponding electric ones. In magnetic dipole transitions, the photon has one unit of net angular momentum just like in electric dipole transitions. However, the photon now has even parity. Therefore magnetic dipole transitions allow the nuclear parity to stay the same.
Transitions in which the nuclear spin changes by more than one unit are possible through emission of a photon with additional orbital angular momentum. That allows a net angular momentum of the photon greater than one. But at a price. Each unit of additional net angular momentum slows down the typical decay rate by roughly 5 orders of magnitude.
The horror story is tantalum-180m. There are at the time of writing
256 ground state nuclei that are classified as stable. And then there
is the excited nucleus tantalum-180m. Stable nuclei should be in
their ground state, because states of higher energy decay into lower
energy ones. But tantalum-180m has never been observed to decay. If
it decays at all, it has been established that its half life cannot be
less than 1![]()
![]()
The tantalum-180 ground state shows no such idiocy. It is unstable as
any self-respecting heavy odd-odd nucleus should be. In fact it
disintegrates within about 8 hours through both electron capture and
beta-minus decay at comparable rates. But tantalum-180m is an excited
state with a humongous spin of 9. Figure 14.56 shows
the excited energy levels of tantalum-180; tantalum-180m is the second
excited energy level. It can only decay to the ![]()
![]()
You might think that tantalum-180m could just disintegrate directly through electron capture or beta decay. But those processes have the same problem. There is just no way for tantalum-180m to get rid of all that spin without emitting particles with unlikely large orbital angular momentum. So tantalum-180m will live forever, spinning too fast to reach the sweet oblivion of the quick death that waits below.
Electric transitions are often generically indicated as ![]()
![]() .
.![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For electric transitions, the nuclear parity changes when ![]()
![]()
That leaves transitions from nuclear spin 0 to nuclear spin 0. Such transitions cannot occur through emission of a photon, period. For such transitions, conservation of angular momentum would require that the photon is emitted without angular momentum. But a photon cannot have zero net angular momentum. You might think that the spin of the photon could be canceled through one unit of orbital angular momentum. However, because the spin and orbital angular momentum of a photon are linked, it turns out that this is not possible, {A.21}.
Decay from an excited state with spin zero to another state that also has spin zero is possible through internal conversion or internal pair production. In principle, it could also be achieved through two-photon emission, but that is a very slow process that has trouble competing with the other two.
One other approximate conservation law might be mentioned here,
isospin. Isospin is conserved by nuclear forces, and its charge
component is conserved by electromagnetic forces, section
14.18. It can be shown that to the extent that isospin is
conserved, certain additional selection rules apply. These involve
the quantum number of square isospin ![]() ,
,
means the difference between the initial and final nuclear states).
Conjugatemeans that the two nuclei have the numbers of protons and neutrons swapped.
Correspondingtransitions means transitions between equivalent levels, as discussed in section 14.18.)
In a nutshell, expect that the transitions will be unexpectedly slow
if the isospin changes by more than one unit. Expect the same for
nuclei with equal numbers of protons and neutrons if the isospin does
not change at all and it is an ![]()
As an example, [31, p. 390], consider the decay of the ![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
Some disclaimers are appropriate for this example. As far as the oxygen transition is concerned, the NuDat 2 [[12]] data do not say what the dominant decay process for the oxygen-14 state is. Nor what the final state is. So it might be another decay process that dominates. The next higher excited state, with 0.75 MeV more energy, decays 100% through proton emission. And two orders of magnitude faster than Weisskopf does seem a lot, figure 14.63.
As far as the nitrogen transition is concerned, the decay processes
are listed in NuDat 2. The decay is almost totally due to proton
emission, not gamma decay. The actual half-life of this state is
0.000 02 fs; the 2.7 fs mentioned above is computed using the given
decay branching ratios. The 2.7 fs is way above the 0.006 fs
Weisskopf estimate, but that is quite common for ![]()
It may be more reasonable to compare the forbidden nitrogen 8 MeV to
2.3 MeV transition to the allowed 8 MeV to ground state, and 8 MeV to
4 MeV transitions. They are all three ![]()
As another example, the nitrogen transition from the ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
More comprehensive data may be found in [48].
An “isomer” is a long lasting excited state of a nucleus. Usually,
an excited nucleus that does not disintegrate through other means will
drop down to lower energies through the emission of photons in the
gamma ray range. It will then end up back in the ground state within
a typical time in terms of fs, or about 1![]()
But sometimes a nucleus gets stuck in a metastable state that takes
far longer to decay. Such a state is called an isomeric state. Krane
[31, p. 174] ballparks the minimum lifetime to be considered
a true isomeric state at roughly 1![]()
![]()
![]()
![]()
![]()
![]()
But then, why would any excited state be able to last very much more
than the typical 1![]()
forbidden,
or using
a better term, hindered.
If an excited state has a very different spin than the ground state, and there are no states in between the two that are more compatible, then that excited state is stuck. But why would low spin states be right next to high spin states? The main reason is found in the shell model, and in particular figure 14.15. According to the shell model, just below the magic numbers of 50, 82, and 126, high spin states are pushed into regions of low spin states by the so-called spin-orbit interaction. That is a recipe for isomerism if there ever was one.
Therefore, it should be expected that there will be many isomers below the magic numbers of 50, 82, and 126. And that these isomers will have the opposite parity of the ground state, because the high spin states are pushed into low spin states of opposite parity.
And so it is. Figure 14.57 shows the half-lifes of the
longest-lasting exited states of even ![]()
![]()
![]()
Figure 14.58 shows the islands for odd ![]() ,
,![]()
For odd-odd nuclei, figure 14.59, the effects of proton and neutron magic numbers get mixed up. Proton and neutron excitations may combine into larger spin changes, providing one possible explanation for the isomers of light nuclei without parity change.
Besides tantalum-180m, which lives forever, also note bismuth-210m in
figure 14.59. Bismuth-210m has the same spin ![]()
For even-even nuclei, figure 14.60, there is very little isomeric activity.
Gamma decay rates can be ballparked using the so-called
Weisskopf estimates:

![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,55...
...put(335,206){\makebox(0,0)[rb]{227}}
\end{picture}}
\end{picture}
\end{figure}](img3510.gif) |
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,26...
...0,0)[rb]{80}}
\put(335,206){\makebox(0,0)[rb]{227}}
\end{picture}
\end{figure}](img3511.gif) |
The estimates are plotted in figure 14.61. For magnetic transitions the better Moszkowski estimates are shown in figure 14.62. (Internal conversion is discussed in subsection 14.20.6, where the ballparks are given.)
A complete derivation and discussion of these estimates can be found {A.25}. Note that many sources have errors in their formulae and/or graphs or use non-SI units, {A.25.9}. The correct formulae in SI units are in {A.25.8}.
These estimates are derived under the assumption that only a single
proton changes states in the transition. They also assume that the
multipole order is the lowest possible, given by the change in nuclear
spin. And that the final state of the proton has angular momentum
![]() .
.
The initial and final proton states assumed in the estimates are
further very simple, {A.25.8}. They are like a shell model
state with a simplified radial dependence. Corrections exist for that
radial dependence too. But the way the estimates are mostly used in
practice is as a reference. The actual decay rate in a transition is
compared to the Weisskopf or Moszkowski estimates. These estimates
are therefore used as units
to express decay rates in.
If there is a big difference, it gives hints about the nature of the
transition process. For example, the actual decay rate is often
orders of magnitude smaller than the estimate. That can indicate that
the state produced by the decay Hamiltonian has only a small
probability of being the correct final nuclear state. In other words,
there may be a poor match-up
or “little
overlap” between the initial and final nuclear states. It is
implicit in the simple proton states used in the estimates that the
state produced by the decay Hamiltonian has a good chance of being
right. But actual ![]()
Conversely, the observed transition rate may be several orders of
magnitude more rapid than the estimate. That may indicate that a lot
of nucleons are involved in the transition. Their contributions can
add up. This is frequently related to shape changes in nonspherical
nuclei. For example, ![]()
Interestingly, ![]()
Finally, what other books do not point out is that there is a problem with electrical transitions in the islands of isomerism. There is serious concern about the correctness of the very Hamiltonian used in such transitions, {N.14}. This problem does not seem to affect magnetic multipole transitions in the nonrelativistic approximation.
Another problem not pointed out in various other books is for magnetic
transitions. Consider the shell model states, figure
14.15. They allow many transitions inside the bands that
by their unit change in angular momentum and unchanged parity are
![]()
![]()
![]()
Note that the single-particle model does give a nontrivial prediction
for say an 2![]()
![]()
![]()
![]()
![]()
This subsection compares the theoretical Weisskopf and Moszkowski estimates of the previous section with actual data. The data are from NuDat 2, [[12]]. The plotted values are a broad but further quite random selection of data of apparently good quality. A more precise description of the data selection procedure is in {N.34}. Internal conversion effects, as discussed in subsection 14.20.6, have been mathematically removed using the conversion constants given by NuDat 2. Computed decay rates were checked against the decay rates in W.u. as given by NuDat 2.
Figures 14.63 and 14.64 show the results. What is plotted
is the half life, scaled to an (harmonic) average nucleus size. In
particular,
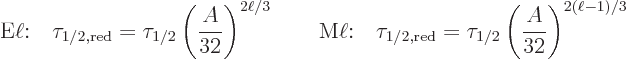
The multipole levels are color coded. The Weisskopf values are shown
as broken lines. The solid lines are an attempt at a “best
guess” based on the single-particle model. For the electric
transitions, they simply use the empirical radial factor
{A.25.8} (A.187). For the magnetic transitions,
the best guess was based on the more accurate Moszkowski estimates.
The empirical radial factor was again used. The momentum factor
{A.25.8} (A.189) at minimum multipole order was
averaged between the proton and neutron values. The ![]()
Symbol size indicates the nucleus size. Symbol shape indicates
whether the numbers of protons and neutrons are even or odd. A minus
sign indicates that the initial parity is odd; otherwise it is even.
The final parity follows from the multipole order and type. An open
symbol center indicates that the multipole level ![]()
Please, your mouth is hanging open. It makes you look very goofy. You can almost pretend that the magnetic data are not really as bad as they look, if you cover up those numbers along the vertical axis with your arm.
There is no doubt that if engineers got data like that, they would conclude that something is terribly and fundamentally wrong. Physicists however pooh-pooh the problems.
First of all, physics textbooks typically only present the ![]()
![]()
only
an order of magnitude or so off.
According to the figures here, this good
agreement
happens only for the ![]()
![]()
![]()
![]()
![]()
Consider now a typical basic nuclear textbook for physicist.
According to the book, disagreements of several orders of magnitude
from theory can happen. The difference between “can
happen” and are normal
is not defined. The
book further explains: “In particular, experimental
disintegration rates smaller than the ones predicted by [the Weisskopf
estimates] can mean that [the Weisskopf radial factor
{A.25.8} (A.187)] is not very reasonable and that
the small overlap of the [initial and final nuclear wave functions]
decreases the values of ![]() .
.
However, the best guess
![]()
And poor overlap
is an easy cop-out since nuclear wave
functions are not known. For example, it does not explain why some
multipole orders like ![]()
Transition rates many orders of magnitude smaller than theory must have a good reason. Random deviations from theory are not a reasonable explanation. Having a transition rate typically four orders of magnitude smaller than a reasonable theoretical estimate is like routinely hitting the bull’s eye of a 10 cm target to within a mm. There must be something causing this.
But what might that be? Conservation of angular momentum and parity
are already fully accounted for. To be sure, conservation of isospin
is not. However, isospin is an approximate symmetry. It is not
accurate enough to explain reductions by 4 or 5 orders of magnitude.
The two examples mentioned in subsection 14.20.2 managed just
1 order of magnitude slow down. And not all ![]()
To be sure, the above arguments implicitly assume that a bull’s eye is hit by an incredibly accurate cancelation of opposite terms in the so-called matrix element that describes transitions. There is an alternate possibility. The final nuclear wave function could be zero where the initial one is nonzero and vice versa. In that case, the integrand in the matrix element is everywhere zero, and no accurate cancellations are needed.
But consider now the top half of figure 14.65. Here mixed
![]()
![]()
overlap
very well. But how then to explain that the
corresponding electric rates are 31 000, 7 800, and 200 times
slower than best guess? The initial and final wave functions
are the same. While there is a different operator sandwiched in
between, {A.25}, the picture still becomes that one
operator apparently achieves a bull’s eye of perfect cancellation.
There should be an explanation.
The example textbook also notes: “Experimental values higher
than predicted by [the Weisskopf estimates] can mean, on the other
hand, that the transition involves the participation of more than one
nucleon or even a collective participation of the whole
nucleus.” The textbook notes in particular that the reason
that most ![]()
This is a well established argument. In principle 50 protons
transitioning could indeed explain why many ![]()
![]()
But there are again some problems. For one, the mixed ![]()
![]()
![]()
Consider also the bottom of figure 14.65. Here mixed
![]()
![]()
![]()
![]()
![]()
It is true that the orbital effect is relatively minor in magnetic
transitions of minimal multipole order, {A.25.8}. But the
transitions given by black symbols with open centers in the bottom of
figure 14.65 are not of minimal multipole order. And in any
case, relatively minor
gets nowhere near to explaining
differences of four or five orders of magnitude in relative decay
rates.
The same problem exists for the idea that the special nature of transitions within rotational bands might somehow be responsible. Surely the idea of rotational bands is not be far accurate enough to explain the humongous differences? And some of the worst offenders in figure 14.65 are definitely not between states in the same rotational band. Those are again the ones where the black symbol has an open center; the nuclear spin does not change in those transitions.
There are 65 randomly chosen ![]()
best guess
theoretical transition rate. That is a
boron-10 transition. (You may have to strain your eyes to see it, it
is such a small nucleus. It is right on top of the best-guess line,
just before 1 MeV.) On the other hand, one transition is slower than
best guess by more than 8 orders of magnitude, and another three are
slower by more than 7 orders of magnitude.
Compare that with the 67 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Also, why do ![]()
![]()
![]()
The example textbook concludes: “In figure [...] one notes
very good agreement between theoretical values and experimental ones
for ![]() .
.![]()
typical
for high multipolarity.
Needless to say, then, the author of this book finds the discussion of measured gamma decay versus theory in standard nuclear text books grossly inadequate, and highly unconvincing where it is given at all. If you feel the same way, see note {N.36} for one alternative idea.
In internal conversion, a nucleus gets rid of excitation energy by
kicking an atomic electron out of the atom. This is most important
for transitions between states of zero spin. For such transitions,
the normal gamma decay process of emitting a photon is not possible
since a photon cannot be emitted with zero angular momentum. However,
the ejected electron, called the “conversion electron,” can keep whatever angular momentum it
has. (For practical purposes, that is zero. Electrons that are not
in s states have negligible probabilility of being found inside the
nucleus.) Transitions in which no angular momentum is emitted by the
nucleus are called ![]()
A ballpark decay rate for ![]()
Note that the first three factors in the expression above look much
like an ![]()
![]()
![]()
Putting in the numbers gives the equivalent of (14.67) as
Table 14.5 shows how the estimate stands up to scrutiny. The
listed ![]()
![]()
![]()
The second-last column in the table shows a scaled half life. It is
scaled to some (harmonic) average nucleus size ![]()
![]()
![]()
![]()
However, the final three nuclei decay much more rapidly than internal
conversion predicts. A second decay process occurs here:
electron-positron pair creation. This requires that the nuclear
energy release ![]()
In transitions other than between states of zero spin, normal gamma decay is possible. But even in those decays, internal conversion and pair production may compete with gamma decay. They are especially important in highly forbidden gamma decays.
The so-called “internal conversion coefficient” ![]()
The following ballpark values for the internal conversion coefficient
in electric and magnetic transitions can be derived ignoring
relativistic effects and electron binding energy:
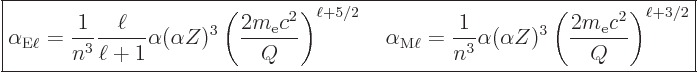 |
(14.71) |
The above estimates are very rough. They are routinely off by a
couple of orders of magnitude. However, they do predict a few correct
trends. Internal conversion is relatively more important compared to
gamma decay if the energy release ![]()
![]()
![]()
![]()
(You might wonder why the earlier ballpark for ![]()
![]()
![]()
![]()
![]()
![]()
Internal conversion is especially useful for investigating nuclei because the conversion coefficients are different for electric and magnetic transitions. Therefore, detailed decay measurements can shed light on the question whether a given transition is an electric or a magnetic one. Since they also depend strongly on the multipole order, they also help establish that. To be sure, the estimates above are not by far accurate enough to do these things. But much more accurate values have been computed using relativistic theories and tabulated.
Internal pair formation supplements internal conversion, [8,7, p. 622]. The pair formation rate is largest where the internal conversion rate is smallest. That is in the region of low atomic number and high transition energies.
One very old reference incorrectly states that internal conversion happens when a gamma ray emitted by the nucleus knocks a surrounding electron out of the atom. Such a process, the photoelectric effect, is in principle possible, but its probability would be negligibly small. Note in particular that in many decays, almost no gamma rays are emitted but lots of conversion electrons. (While the interaction between the nucleus and the conversion electron is of course caused by photons, these are virtual photons. They would not come out of the nucleus even if you stripped away the atomic electrons.)
It may be noted that internal conversion
is not unique
to nuclei. Energetic atomic electron transitions can also get rid of
their energy by ejection of another electron. The ejected electrons
are called “Auger electrons.” They are named after the physicist Auger, who
was the first man to discover the process. (Some unscrupulous woman,
Lise Meitner, had discovered and published it earlier, selfishly
attempting to steal Auger’s credit, {N.35}). In
fact, internal conversion can give rise to additional Auger electrons
as other electrons rush in to fill the internal converion electron
hole. And so can electron capture.