A.28 WKB The­ory of Nearly Clas­si­cal Mo­tion

WKB the­ory pro­vides sim­ple ap­prox­i­mate so­lu­tions for the en­ergy eigen­func­tions when the con­di­tions are al­most clas­si­cal, like for the wave pack­ets of chap­ter 7.11. The ap­prox­i­ma­tion is named af­ter Wentzel, Kramers, and Bril­louin, who re­fined the ideas of Li­ou­ville and Green. The ban­dit sci­en­tist Jef­freys tried to rob WKB of their glory by do­ing the same thing two years ear­lier, and is justly de­nied all credit.

Fig­ure A.16: Har­monic os­cil­la­tor po­ten­tial en­ergy $V$, eigen­func­tion $h_{50}$, and its en­ergy $E_{50}$.

The WKB ap­prox­i­ma­tion is based on the rapid spa­tial vari­a­tion of en­ergy eigen­func­tions with al­most macro­scopic en­er­gies. As an ex­am­ple, fig­ure A.16 shows the har­monic os­cil­la­tor en­ergy eigen­func­tion $h_{50}$. Its en­ergy $E_{50}$ is hun­dred times the ground state en­ergy. That makes the ki­netic en­ergy $E-V$ quite large over most of the range, and that in turn makes the lin­ear mo­men­tum large. In fact, the clas­si­cal New­ton­ian lin­ear mo­men­tum $p_{\rm {c}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $mv$ is given by

$$\fbox{$\displaystyle p_{\rm{c}} \equiv \sqrt{2m(E-V)} $} %$$ (A.207)

In quan­tum me­chan­ics, the large mo­men­tum im­plies rapid os­cil­la­tion of the wave func­tion: quan­tum me­chan­ics as­so­ciates the lin­ear mo­men­tum with the op­er­a­tor $\hbar{\rm d}$$\raisebox{.5pt}{$/$}$​${\rm i}{\rm d}{x}$ that de­notes spa­tial vari­a­tion.

The WKB ap­prox­i­ma­tion is most ap­peal­ing in terms of the clas­si­cal mo­men­tum $p_{\rm {c}}$ as de­fined above. To find its form, in the Hamil­ton­ian eigen­value prob­lem

$$-\frac{\hbar^2}{2m} \frac{{\rm d}^2\psi}{{\rm d}x^2} + V\psi = E\psi$$

take the $V\psi$ term to the other side and then rewrite $E-V$ in terms of the clas­si­cal lin­ear mo­men­tum. That pro­duces

$$\frac{{\rm d}^2\psi}{{\rm d}x^2} = - \frac{p_{\rm {c}}^2}{\hbar^2}\psi %$$ (A.208)

Now un­der al­most clas­si­cal con­di­tions, a sin­gle pe­riod of os­cil­la­tion of the wave func­tion is so short that nor­mally $p_{\rm {c}}$ is al­most con­stant over it. Then by ap­prox­i­ma­tion the so­lu­tion of the eigen­value prob­lem over a sin­gle pe­riod is sim­ply an ar­bi­trary com­bi­na­tion of two ex­po­nen­tials,

$$\psi \sim c_{\rm {f}} e^{{\rm i}p_{\rm {c}} x/\hbar} + c_{\rm {b}} e^{-{\rm i}p_{\rm {c}} x/\hbar}$$

where the con­stants $c_{\rm {f}}$ and $c_{\rm {b}}$ are ar­bi­trary. (The sub­scripts de­note whether the wave speed of the cor­re­spond­ing term is for­ward or back­ward.)

It turns out that to make the above ex­pres­sion work over more than one pe­riod, it is nec­es­sary to re­place $p_{\rm {c}}x$ by the an­ti­deriv­a­tive $\int{p}_{\rm {c}}{ \rm d}{x}$. Fur­ther­more, the con­stants $c_{\rm {f}}$ and $c_{\rm {b}}$ must be al­lowed to vary from pe­riod to pe­riod pro­por­tional to 1$\raisebox{.5pt}{$/$}$​$\sqrt{p_{\rm {c}}}$.

In short, the WKB ap­prox­i­ma­tion of the wave func­tion is, {D.46}:

$$\fbox{$\displaystyle \mbox{classical WKB:} \qquad \psi \a... ...\theta \equiv \frac{1}{\hbar} \int p_{\rm{c}} { \rm d}x $} %$$ (A.209)

where $C_{\rm {f}}$ and $C_{\rm {b}}$ are now true con­stants.

If you ever glanced at notes such as {D.12}, {D.14}, and {D.15}, in which the eigen­func­tions for the har­monic os­cil­la­tor and hy­dro­gen atom were found, you rec­og­nize what a big sim­pli­fi­ca­tion the WKB ap­prox­i­ma­tion is. Just do the in­te­gral for $\theta$ and that is it. No elab­o­rate trans­for­ma­tions and power se­ries to grind down. And the WKB ap­prox­i­ma­tion can of­ten be used where no ex­act so­lu­tions ex­ist at all.

In many ap­pli­ca­tions, it is more con­ve­nient to write the WKB ap­prox­i­ma­tion in terms of a sine and a co­sine. That can be done by tak­ing the ex­po­nen­tials apart us­ing the Euler for­mula (2.5). It pro­duces

$$\fbox{$\displaystyle \mbox{rephrased WKB:} \qquad \psi \a... ...\theta \equiv \frac{1}{\hbar} \int p_{\rm{c}} { \rm d}x $} %$$ (A.210)

The con­stants $C_{\rm {c}}$ and $C_{\rm {s}}$ are re­lated to the orig­i­nal con­stants $C_{\rm {f}}$ and $C_{\rm {b}}$ as

$$\fbox{$\displaystyle C_{\rm{c}} = C_{\rm{f}} + C_{\rm{b}} ... ...\textstyle\frac{1}{2}} (C_{\rm{c}} + {\rm i}C_{\rm{s}}) $} %$$ (A.211)

which al­lows you to con­vert back and for­ward be­tween the two for­mu­la­tions as needed. Do note that ei­ther way, the con­stants de­pend on what you chose for the in­te­gra­tion con­stant in the $\theta$ in­te­gral.

As an ap­pli­ca­tion, con­sider a par­ti­cle stuck be­tween two im­pen­e­tra­ble walls at po­si­tions $x_1$ and $x_2$. An ex­am­ple would be the par­ti­cle in a pipe that was stud­ied way back in chap­ter 3.5. The wave func­tion $\psi$ must be­come zero at both $x_1$ and $x_2$, since there is zero pos­si­bil­ity of find­ing the par­ti­cle out­side the im­pen­e­tra­ble walls. It is now smart to chose the in­te­gra­tion con­stant in $\theta$ so that $\theta_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0. In that case, $C_{\rm {c}}$ must be zero for $\psi$ to be zero at $x_1$, (A.210). The wave func­tion must be just the sine term. Next, for $\psi$ also to be zero at $x_2$, $\theta_2$ must be a whole mul­ti­ple $n$ of $\pi$, be­cause that are the only places where sines are zero. So $\theta_2-\theta_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ $n\pi$, which means that

$$\fbox{$\displaystyle \mbox{particle between impenetrable w... ..._{\rm{c}}({\underline x}) { \rm d}{\underline x}= n \pi $} %$$ (A.212)

Re­call that $p_{\rm {c}}$ was $\sqrt{2m(E-V)}$, so this is just an equa­tion for the en­ergy eigen­val­ues. It is an equa­tion in­volv­ing just an in­te­gral; it does not even re­quire you to find the cor­re­spond­ing eigen­func­tions!

It does get a bit more tricky for a case like the har­monic os­cil­la­tor where the par­ti­cle is not caught be­tween im­pen­e­tra­ble walls, but merely pre­vented to es­cape by a grad­u­ally in­creas­ing po­ten­tial. Clas­si­cally, such a par­ti­cle would still be rig­or­ously con­strained be­tween the so called “turn­ing points” where the po­ten­tial en­ergy $V$ be­comes equal to the to­tal en­ergy $E$, like the points 1 and 2 in fig­ure A.16. But as the fig­ure shows, in quan­tum me­chan­ics the wave func­tion does not be­come zero at the turn­ing points; there is some chance for the par­ti­cle to be found some­what be­yond the turn­ing points.

A fur­ther com­pli­ca­tion arises since the WKB ap­prox­i­ma­tion be­comes in­ac­cu­rate in the im­me­di­ate vicin­ity of the turn­ing points. The prob­lem is the re­quire­ment that the clas­si­cal mo­men­tum can be ap­prox­i­mated as a nonzero con­stant on a small scale. At the turn­ing points the mo­men­tum be­comes zero and that ap­prox­i­ma­tion fails.

How­ever, it is pos­si­ble to solve the Hamil­ton­ian eigen­value prob­lem near the turn­ing points as­sum­ing that the po­ten­tial en­ergy is not con­stant, but varies ap­prox­i­mately lin­early with po­si­tion, {A.29}. Do­ing so and fix­ing up the WKB so­lu­tion away from the turn­ing points pro­duces a sim­ple re­sult. The clas­si­cal WKB ap­prox­i­ma­tion re­mains a sine, but at the turn­ing points, $\sin\theta$ stays an an­gu­lar amount $\pi$$\raisebox{.5pt}{$/$}$​4 short of be­com­ing zero. (Or to be pre­cise, it just seems to stay $\pi$$\raisebox{.5pt}{$/$}$​4 short, be­cause the clas­si­cal WKB ap­prox­i­ma­tion is no longer valid at the turn­ing points.) As­sum­ing that there are turn­ing points with grad­u­ally in­creas­ing po­ten­tial at both ends of the range, like for the har­monic os­cil­la­tor, the to­tal an­gu­lar range will be short by an amount $\pi$$\raisebox{.5pt}{$/$}$​2.

There­fore, the ex­pres­sion for the en­ergy eigen­val­ues be­comes:

$$\fbox{$\displaystyle \mbox{particle trapped between turnin... ...,\rm d}{\underline x} = (n-{\textstyle\frac{1}{2}}) \pi $} %$$ (A.213)

The WKB ap­prox­i­ma­tion works fine in re­gions where the to­tal en­ergy $E$ is less than the po­ten­tial en­ergy $V$. The clas­si­cal mo­men­tum $p_{\rm {c}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\sqrt{2m(E-V)}$ is imag­i­nary in such re­gions, re­flect­ing the fact that clas­si­cally the par­ti­cle does not have enough en­ergy to en­ter them. But, as the nonzero wave func­tion be­yond the turn­ing points in fig­ure A.16 shows, quan­tum me­chan­ics does al­low some pos­si­bil­ity for the par­ti­cle to be found in re­gions where $E$ is less than $V$. It is loosely said that the par­ti­cle can tun­nel through, af­ter a pop­u­lar way for crim­i­nals to es­cape from jail. To use the WKB ap­prox­i­ma­tion in these re­gions, just rewrite it in terms of the mag­ni­tude $\vert p_{\rm {c}}\vert$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\sqrt{2m(V-E)}$ of the clas­si­cal mo­men­tum:

$$\fbox{$\displaystyle \mbox{tunneling WKB:}\qquad \psi \ap... ...iv \frac{1}{\hbar} \int \vert p_{\rm{c}}\vert { \rm d}x $} %$$ (A.214)

Note that $\gamma$ is the equiv­a­lent of the an­gle $\theta$ in the clas­si­cal ap­prox­i­ma­tion.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The WKB ap­prox­i­ma­tion ap­plies to sit­u­a­tions of al­most macro­scopic en­ergy.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The WKB so­lu­tion is de­scribed in terms of the clas­si­cal mo­men­tum $p_{\rm {c}}$ $\vphantom0\raisebox{1.5pt}{$\equiv$}$ $\sqrt{2m(E-V)}$ and in par­tic­u­lar its an­ti­deriv­a­tive $\theta$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int{p}_{\rm {c}}{ \rm d}{x}$$\raisebox{.5pt}{$/$}$​$\hbar$.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The wave func­tion can be writ­ten as (A.209) or (A.210), what­ever is more con­ve­nient.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

For a par­ti­cle stuck be­tween im­pen­e­tra­ble walls, the en­ergy eigen­val­ues can be found from (A.212).

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

For a par­ti­cle stuck be­tween a grad­u­ally in­creas­ing po­ten­tial at both sides, the en­ergy eigen­val­ues can be found from (A.213).

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The tun­nel­ing wave func­tion in re­gions that clas­si­cally the par­ti­cle is for­bid­den to en­ter can be ap­prox­i­mated as (A.214). It is in terms of the an­ti­deriv­a­tive $\gamma$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int\vert p_{\rm {c}}\vert{ \rm d}{x}$$\raisebox{.5pt}{$/$}$​$\hbar$.

A.28 Re­view Ques­tions

1.

Use the equa­tion

$$\frac{1}{\hbar} \int_{{\underline x}=x_1}^{x_2} p_{\rm {c}}({\underline x}) { \rm d}{\underline x}= n \pi$$

to find the WKB ap­prox­i­ma­tion for the en­ergy lev­els of a par­ti­cle stuck in a pipe of chap­ter 3.5.5. The po­ten­tial $V$ is zero in­side the pipe, given by 0 $\raisebox{-.3pt}{$\leqslant$}$ $x$ $\raisebox{-.3pt}{$\leqslant$}$ $\ell_x$

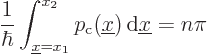
In this case, the WKB ap­prox­i­ma­tion pro­duces the ex­act re­sult, since the clas­si­cal mo­men­tum re­ally is con­stant. If there was a force field in the pipe, the so­lu­tion would only be ap­prox­i­mate.

So­lu­tion wkb-a

2.

Use the equa­tion

$$\frac{1}{\hbar} \int_{{\underline x}=x_1}^{x_2} p_{\rm {c}}(... ...e x}) { \rm d}{\underline x}= (n-{\textstyle\frac{1}{2}}) \pi$$

to find the WKB ap­prox­i­ma­tion for the en­ergy lev­els of the har­monic os­cil­la­tor. The po­ten­tial en­ergy is ${\textstyle\frac{1}{2}}m\omega{x}^2$ where the con­stant $\omega$ is the clas­si­cal nat­ural fre­quency. So the to­tal en­ergy, ex­pressed in terms of the turn­ing points $x_2$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-x_1$ at which $E$ $\vphantom0\raisebox{1.5pt}{$=$}$ $V$, is $E$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\textstyle\frac{1}{2}}m\omega{x_2}^2$.

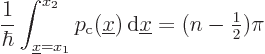
In this case too, the WKB ap­prox­i­ma­tion pro­duces the ex­act en­ergy eigen­val­ues. That, how­ever, is just a co­in­ci­dence; the clas­si­cal WKB wave func­tions are cer­tainly not ex­act; they be­come in­fi­nite at the turn­ing points. As the ex­am­ple $h_{50}$ above shows, the true wave func­tions most def­i­nitely do not.

So­lu­tion wkb-b