| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
A.28.2 Solution wkb-b
Question:
Use the equation
to find the WKB approximation for the energy levels of the harmonic oscillator. The potential energy is  where the constant
where the constant 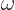 is the classical natural frequency. So the total energy, expressed in terms of the turning points
is the classical natural frequency. So the total energy, expressed in terms of the turning points 

 at which
at which 

 , is
, is 

 .
.
In this case too, the WKB approximation produces the exact energy eigenvalues. That, however, is just a coincidence; the classical WKB wave functions are certainly not exact; they become infinite at the turning points. As the example  above shows, the true wave functions most definitely do not.
above shows, the true wave functions most definitely do not.
Answer:
Substituting in 

 , with
, with 

 and
and 

 , produces
, produces
The integral can be done by making the substitution 

 :
:
and the remaining integral is  :
:
So, since 

 , the energy levels are found to be
, the energy levels are found to be 

 . That is exact; the fact that in this case the values of
. That is exact; the fact that in this case the values of 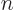 are counted from one instead of zero is just a matter of notations. Despite the imperfect wave functions, it sure is a lot simpler than the exact derivation of chapter 4.1 as found in its note.
are counted from one instead of zero is just a matter of notations. Despite the imperfect wave functions, it sure is a lot simpler than the exact derivation of chapter 4.1 as found in its note.

![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ,
,
