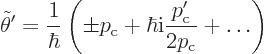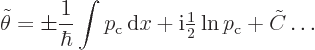| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.46 Derivation of the WKB approximation
The purpose in this note is to derive an approximate solution to the
Hamiltonian eigenvalue problem
where the classical momentum 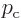

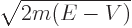 is a known
function for given energy. The approximation is to be valid when the
values of
is a known
function for given energy. The approximation is to be valid when the
values of 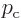

 are large. In quantum terms, you can
think of that as due to an energy that is macroscopically large. But
to do the mathematics, it is easier to take a macroscopic point of
view; in macroscopic terms,
are large. In quantum terms, you can
think of that as due to an energy that is macroscopically large. But
to do the mathematics, it is easier to take a macroscopic point of
view; in macroscopic terms, 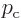

 is large because
Planck’s constant
is large because
Planck’s constant  is so small.
is so small.
Since either way 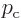

 is a large quantity, for the left hand
side of the Hamiltonian eigenvalue problem above to balance the right
hand side, the wave function must vary rapidly with position.
Something that varies rapidly and nontrivially with position tends to
be hard to analyze, so it turns out to be a good idea to write the
wave function as an exponential,
is a large quantity, for the left hand
side of the Hamiltonian eigenvalue problem above to balance the right
hand side, the wave function must vary rapidly with position.
Something that varies rapidly and nontrivially with position tends to
be hard to analyze, so it turns out to be a good idea to write the
wave function as an exponential,
and then approximate the argument 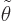 of that exponential.
of that exponential.
To do so, first the equation for 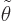 will be needed.
Taking derivatives of
will be needed.
Taking derivatives of  using the chain rule gives in terms of
using the chain rule gives in terms of
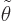
Then plugging  and its second derivative above into the
Hamiltonian eigenvalue problem and cleaning up gives:
and its second derivative above into the
Hamiltonian eigenvalue problem and cleaning up gives:
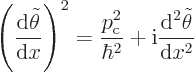 |
(D.30) |
For a given energy, 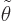 will depend on both what
will depend on both what  is and
what
is and
what  is. Now, since
is. Now, since  is small, mathematically it
simplifies things if you expand
is small, mathematically it
simplifies things if you expand 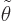 in a power series with
respect to
in a power series with
respect to  :
:
You can think of this as writing 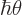 as a Taylor series in
as a Taylor series in
 . The coefficients
. The coefficients 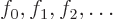 will depend on
will depend on
 . Since
. Since  is small, the contribution of
is small, the contribution of 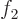 and
further terms to
and
further terms to  is small and can be ignored; only
is small and can be ignored; only 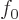 and
and
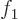 will need to be figured out.
will need to be figured out.
Plugging the power series into the equation for 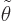 produces
produces
where primes denote  -derivatives and the dots stand for powers of
-derivatives and the dots stand for powers of
 greater than
greater than 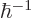 that will not be needed. Now for
two power series to be equal, the coefficients of each individual
power must be equal. In particular, the coefficients of 1
that will not be needed. Now for
two power series to be equal, the coefficients of each individual
power must be equal. In particular, the coefficients of 1
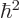 must be equal,
must be equal, 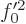

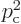 , so there are two
possible solutions
, so there are two
possible solutions
For the coefficients of 1
 to be equal,
to be equal, 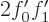

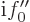 , or plugging in the solution for
, or plugging in the solution for 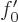 ,
,
It follows that the  -derivative of
-derivative of 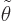 is given by
is given by
and integrating gives 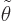 as
as
where 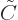 is an integration constant. Finally,
is an integration constant. Finally,
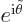 now gives the two terms in the WKB solution, one
for each possible sign, with
now gives the two terms in the WKB solution, one
for each possible sign, with 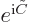 equal to the constant
equal to the constant
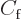 or
or 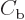 .
.
![]()
![]()
![]()
![]()
![]()
![]()
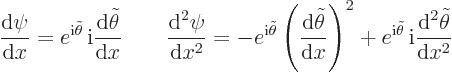
![]()
![]()
![]()
![]()
![]()
![]() :
:![]()
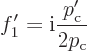
![]() -
-![]()