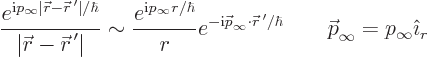| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.47 Born differential cross section
This note derives the Born differential cross section of addendum
{A.30}.
The general idea is to approximate (A.228) for large distances
 . Then the asymptotic constant
. Then the asymptotic constant  in
(A.216) can be identified, which gives the differential
cross section according to (A.218). Note that the Born
approximation took the asymptotic constant
in
(A.216) can be identified, which gives the differential
cross section according to (A.218). Note that the Born
approximation took the asymptotic constant 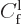 equal
to one for simplicity.
equal
to one for simplicity.
The main difficulty in approximating (A.228) for large
distances  is the argument of the exponential in the fraction. It
is not accurate enough to just say that
is the argument of the exponential in the fraction. It
is not accurate enough to just say that 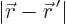 is
approximately equal to
is
approximately equal to  . You need the more accurate
approximation
. You need the more accurate
approximation
The final approximation is from taking a factor 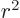 out of the
square root and then approximating the rest by a Taylor series. Note
that the fraction in the final term is the unit vector
out of the
square root and then approximating the rest by a Taylor series. Note
that the fraction in the final term is the unit vector 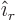 in
the
in
the  -direction.
-direction.
It follows that
Also, in the second exponential, since 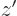

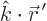 ,
,
Writing out the complete expression (A.228) and comparing
with (A.216) gives the constant 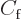 and hence
the differential cross section.
and hence
the differential cross section.
![]() .
.![]()
![]()
![]()
![]()
![]() .
.