| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
A.30 Three-dimensional scattering
This note introduces some of the general concepts of three-dimensional
scattering, in case you run into them. For more details and actual
examples, a quantum mechanics text for physicists will need to be
consulted; it is a big thing for them.
Figure A.21:
Scattering of a beam off a target.
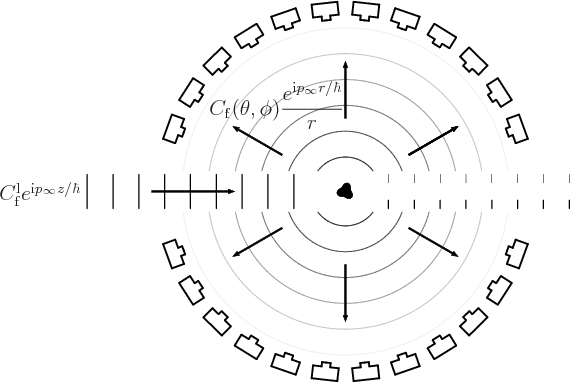 |
The basic idea is as sketched in figure A.21. A beam of
particles is sent in from the far left towards a three-dimensional
target. Part of the beam hits the target and is scattered, to
be picked up by surrounding detection equipment.
It will be assumed that the collision with the target is elastic, and
that the particles in the beam are sufficiently light that they
scatter off the target without transferring kinetic energy to it. In
that case, the target can be modeled as a steady potential energy
field. And if the target and/or incoming particles are electrically
neutral, it can also be assumed that the potential energy decays
fairly quickly to zero away from the target. (In fact, a lot of
results in this note turn out not apply to a slowly decaying potential
like the Coulomb one.)
It is convenient to use a spherical coordinate system
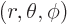 with its origin at the scattering object and with
its axis aligned with the direction of the incoming beam. Since the
axis of a spherical coordinate system is usually called the
with its origin at the scattering object and with
its axis aligned with the direction of the incoming beam. Since the
axis of a spherical coordinate system is usually called the  -axis,
the horizontal coordinate will now be indicated as
-axis,
the horizontal coordinate will now be indicated as  , not
, not  like in the one-dimensional analysis done earlier.
like in the one-dimensional analysis done earlier.
In the energy eigenfunctions, the incoming particle beam can be
represented as a one-dimensional wave. However, unlike for the one-dimensional
scattering of figure 7.22, now the wave is not just
scattered to the left and right, but in all directions, in other words
to all angles  and
and  . The far-field behavior of
the energy eigenfunctions is
. The far-field behavior of
the energy eigenfunctions is
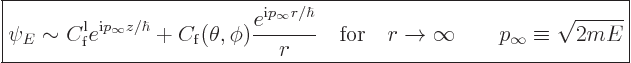 |
(A.216) |
Here  is the kinetic energy of the incoming particles and
is the kinetic energy of the incoming particles and  the
mass. Therefore
the
mass. Therefore 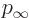 is what classical physics would take to be
the momentum of the particles at infinity. The first term in the far
field behavior allows the incoming particles to be described, as well
as the same particles going out again unperturbed. If some joker
removes the target, that is all there is.
is what classical physics would take to be
the momentum of the particles at infinity. The first term in the far
field behavior allows the incoming particles to be described, as well
as the same particles going out again unperturbed. If some joker
removes the target, that is all there is.
The second term describes the outgoing scattered particles. The
constant 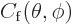 is called the “scattering amplitude.” The second term also contains a factor
is called the “scattering amplitude.” The second term also contains a factor
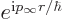 consistent with wave packets that move
radially away from the target in the far field.
consistent with wave packets that move
radially away from the target in the far field.
Finally, the second term contains a factor 1/ . Therefore the
magnitude of the second term decreases with the distance
. Therefore the
magnitude of the second term decreases with the distance  from the
target. This happens because the probability of finding a particle in
a given detection area should decrease with distance. Indeed, the
total detection area is
from the
target. This happens because the probability of finding a particle in
a given detection area should decrease with distance. Indeed, the
total detection area is 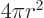 , where
, where  is the distance
at which the detectors are located. That increases proportional to
is the distance
at which the detectors are located. That increases proportional to
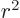 , and the total number of particles to detect per unit time
is the same regardless of where the detectors are located. Therefore
the probability of finding a particle per unit area should decrease
proportional to 1/
, and the total number of particles to detect per unit time
is the same regardless of where the detectors are located. Therefore
the probability of finding a particle per unit area should decrease
proportional to 1/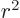 . Since the probability of finding a
particle is proportional to the square of the wave function, the wave
function itself must be proportional to 1/
. Since the probability of finding a
particle is proportional to the square of the wave function, the wave
function itself must be proportional to 1/ . The second term
above makes it so.
. The second term
above makes it so.
Consider now the number of particles that is detected in a given small
detection area 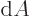 . The scattered stream of particles
moving towards the detection area has a velocity
. The scattered stream of particles
moving towards the detection area has a velocity 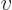

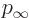

 . Therefore in a time interval
. Therefore in a time interval 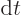 ,
the detection area samples a volume of the scattered particle stream
equal to
,
the detection area samples a volume of the scattered particle stream
equal to 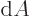

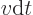 . The chances of finding
particles are proportional to the square magnitude of the wave
function times that volume. Using the asymptotic wave function above,
the number of particles detected will be
. The chances of finding
particles are proportional to the square magnitude of the wave
function times that volume. Using the asymptotic wave function above,
the number of particles detected will be
The constant includes the factor 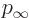

 . The constant
must also account for the fact that the wave function is not
normalized, and that there is a continuous stream of particles to be
found, rather than just one particle.
. The constant
must also account for the fact that the wave function is not
normalized, and that there is a continuous stream of particles to be
found, rather than just one particle.
According to the above expression, the number of particles detected in
a given area 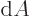 is proportional to its three-dimensional angular
extent
is proportional to its three-dimensional angular
extent
This is the so-called “solid angle” occupied by the detection area element. It is the
three-dimensional generalization of two-dimensional angles. In two
dimensions, an element of a circle with arc length 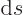 occupies
an angle
occupies
an angle 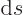

 when expressed in radians. Similarly, in three
dimensions, an element of a sphere with area
when expressed in radians. Similarly, in three
dimensions, an element of a sphere with area 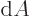 occupies a solid
angle
occupies a solid
angle 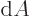

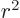 when expressed in “steradians.”
when expressed in “steradians.”
In those terms, the number 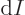 of particles detected in an
infinitesimal solid angle
of particles detected in an
infinitesimal solid angle 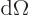 is
is
As noted, the constant of proportionality depends on the rate at which
particles are sent at the target. The more particles are sent at the
target, the more will be deflected. The number of particles in the
incoming beam per unit beam cross-sectional area and per unit time is
called the “luminosity” of the beam. It is related to the square of the
wave function of the incoming beam through the relation
Here 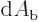 is a cross sectional area element of the
incoming particle beam and
is a cross sectional area element of the
incoming particle beam and 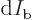 the number of particles
passing through that area.
the number of particles
passing through that area.
Physicist like to relate the scattered particle flow in a given
infinitesimal solid angle 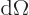 to an equivalent incoming beam
area
to an equivalent incoming beam
area 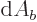 through which the same number of particles flow.
Therefore they define the so-called “differential cross-section” as
through which the same number of particles flow.
Therefore they define the so-called “differential cross-section” as
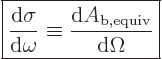 |
(A.217) |
The quantity 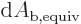 can be thought of as the
infinitesimal area of the incoming beam that ends up in the
infinitesimal solid angle
can be thought of as the
infinitesimal area of the incoming beam that ends up in the
infinitesimal solid angle 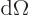 . So the differential
cross-section is a scattered particle density expressed in suitable
terms.
. So the differential
cross-section is a scattered particle density expressed in suitable
terms.
Note how well chosen the term “differential
cross-section” really is. If physicists had called it
something like scattered cross-section density,
or
even simply scattered cross-section,
nonexperts would
probably have a pretty good guess what physicists were talking about.
But cross section
by itself can mean anything. There
is nothing in the term to indicate that it is a measure for how many
particles are scattered. And preceding it by
differential
is a stroke of genius because it is not a
differential, it is a differential quotient. This will confuse
mathematically literate nonexperts even more.
The differential cross section does not depend on how many particles
are sent at the target, nor on wave function normalization. Following
the expressions for the particle flows given above, the differential
cross section is simply
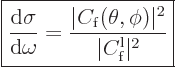 |
(A.218) |
Moreover, the particle flow in an incoming beam area 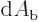 may be measured using the same experimental techniques as are used to
measure the deflected particle flow. Various systematic errors in the
experimental method will then cancel in the ratio, giving more
accurate values.
may be measured using the same experimental techniques as are used to
measure the deflected particle flow. Various systematic errors in the
experimental method will then cancel in the ratio, giving more
accurate values.
The total area of the incoming beam that gets scattered is called the
“total cross-section” 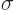 :
:
 |
(A.219) |
Of course, the name is quite below the normal standards of physicists,
since it really is a total cross-section. Fortunately, physicist are
clever enough not to say what cross section it is, and cross-section
can mean many things. Also, by using the symbol 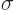 instead of
something logical like
instead of
something logical like 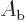 for the differential
cross-section, physicists do their best to reduce the damage as well
as possible.
for the differential
cross-section, physicists do their best to reduce the damage as well
as possible.
If you remain disappointed in physicists, take some comfort in the
following term for scattering that can be described using classical
mechanics: the “impact parameter.” If you guess that it describes the local
physics of the particle impact process, it is really hilarious to
physicists. Instead, think centerline offset;
it
describes the location relative to the centerline of the incoming beam
at which the particles come in; it has no direct relation whatsoever
to what sort of impact (if any) these particles end up experiencing.
The total cross section can be found by integrating the differential
cross section over all deflection angles:
In spherical coordinates this can be written out explicitly as
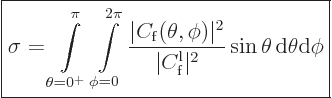 |
(A.220) |
A.30.1 Partial wave analysis
Jim Napolitano from RPI and Cornell notes:
The term Partial Wave Analysis
is poorly defined and
overused.
Gee, what a surprise! For one, they are component waves, not partial
waves. But you already componently assumed that they might be.
This discussion will restrict itself to spherically symmetric
scattering potentials. In that case, the analysis of the energy
eigenfunctions can be done much like the analysis of the hydrogen atom
of chapter 4.3. However, the boundary conditions at
infinity will be quite different; the objective is not to describe
bound particles, but particles that come in from infinity with
positive kinetic energy and are scattered back to infinity. Also, the
potential will of course not normally be a Coulomb one.
But just like for the hydrogen atom, the energy eigenfunctions can be
taken to be radial functions times spherical harmonics 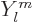 :
:
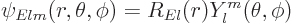 |
(A.221) |
These energy eigenfunctions have definite angular momentum in the
 -direction
-direction 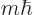 , as well definite square angular momentum
, as well definite square angular momentum
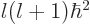 . The radial functions
. The radial functions 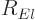 will not be the
same as the hydrogen
will not be the
same as the hydrogen 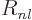 ones.
ones.
The incoming plane wave 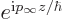 has zero angular
momentum in the
has zero angular
momentum in the  -direction. Unfortunately, it does not have
definite square angular momentum. Instead, it can be written as a
linear combination of free-space energy eigenfunctions with different
values of
-direction. Unfortunately, it does not have
definite square angular momentum. Instead, it can be written as a
linear combination of free-space energy eigenfunctions with different
values of  , hence with different square angular momentum:
, hence with different square angular momentum:
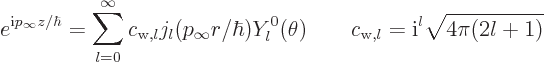 |
(A.222) |
See {A.6} for a derivation and the precise form of
the spherical Bessel functions
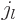 .
.
Now finding the complete energy eigenfunction corresponding to the
incoming wave directly is typically awkward, especially analytically.
Often it is easier to solve the problem for each term in the above sum
separately and then add these solutions all together. That is where
the name partial wave analysis
comes from. Each term
in the sum corresponds to a partial wave, if you use sufficiently
lousy terminology.
The partial wave analysis requires that for each term in the sum, an
energy eigenfunction is found of the form 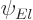

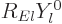 . The required behavior of this eigenfunction in
the far field is
. The required behavior of this eigenfunction in
the far field is
![\begin{displaymath}
\fbox{$\displaystyle
\psi_{El} \sim
\left[c_{{\rm{w}},l}...
...hbar)\right]
Y_l^0(\theta) \qquad\mbox{for } r\to\infty
$} %
\end{displaymath}](img5122.gif) |
(A.223) |
Here the first term is the component of the incoming plane wave
corresponding to spherical harmonic 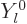 . The second term
represents the outgoing deflected particles. The value of the
coefficient
. The second term
represents the outgoing deflected particles. The value of the
coefficient 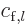 is determined in the solution process.
is determined in the solution process.
Note that the above far field behavior is quite similar to that of the
complete energy eigenfunction as given earlier in (A.216).
However, here the coefficient 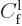 was set to 1 for
simplicity. Also, the radial part of the reflected wave function was
written using a
was set to 1 for
simplicity. Also, the radial part of the reflected wave function was
written using a Hankel function of the first kind
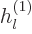 . This Hankel function produces the same
. This Hankel function produces the same
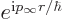

 radial behavior as the second term in
(A.216), {A.6} (A.25).
However, the Hankel function has the advantage that it becomes exact
as soon as the scattering potential becomes zero. It is not just
valid at very large
radial behavior as the second term in
(A.216), {A.6} (A.25).
However, the Hankel function has the advantage that it becomes exact
as soon as the scattering potential becomes zero. It is not just
valid at very large  like the bare exponential.
like the bare exponential.
To be sure, for a slowly decaying potential like the Coulomb one, the
Hankel function is no better than the exponential. However, the
Hankel function is very closely related to the Bessel function
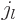 , {A.6}, allowing various helpful results
to be found in table books. If the potential energy is piecewise
constant, it is even possible to solve the complete problem using
Bessel and Hankel functions. These functions can be tied together at
the jumps in potential in a way similar to addendum
{A.27}.
, {A.6}, allowing various helpful results
to be found in table books. If the potential energy is piecewise
constant, it is even possible to solve the complete problem using
Bessel and Hankel functions. These functions can be tied together at
the jumps in potential in a way similar to addendum
{A.27}.
In terms of the asymptotic behavior above, the differential cross
section is
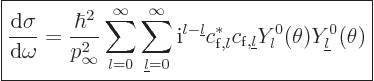 |
(A.224) |
This can be verified using {A.6} (A.25),
(A.216), and (A.218). The Bessel functions form
the incoming wave and do not contribute. For the total cross-section,
note that the spherical harmonics are orthonormal, so
One special case is worth mentioning. Consider particles of such low
momentum that their typical quantum wave length,
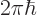

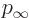 , is gigantic compared to the radial size
of the scattering potential. Particles of such large wave lengths do
not notice the fine details of the scattering potential at all.
Conversely, normally the scattering potential only
, is gigantic compared to the radial size
of the scattering potential. Particles of such large wave lengths do
not notice the fine details of the scattering potential at all.
Conversely, normally the scattering potential only
notices
the incoming partial wave with 
 0.
That is because the Bessel functions are proportional to
0.
That is because the Bessel functions are proportional to
for small arguments. If the wave length is large compared to the
typical radial size  of the scattering potential, this is
negligible unless
of the scattering potential, this is
negligible unless 
 0. Now
0. Now 
 0 corresponds to a wave
function that is the same in all directions; it is proportional to the
constant spherical harmonic
0 corresponds to a wave
function that is the same in all directions; it is proportional to the
constant spherical harmonic 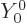 . If only the partial wave
that is the same in all directions gets scattered, then the particles
get scattered equally in all directions (if they get scattered at
all.)
. If only the partial wave
that is the same in all directions gets scattered, then the particles
get scattered equally in all directions (if they get scattered at
all.)
Coincidently, equal scattering in all directions also happens in
another case: scattering of classical point particles from a hard
elastic sphere. That is very much the opposite case, because
negligible uncertainty in position requires high, not low, energy of
the particles. In any case, the similarity between the two cases is
is superficial. If a beam of classical particles is directed at a
hard sphere, only an area of the beam equal to the frontal area of the
sphere gets scattered. But if you work out the scattering of
low-energy quantum particles from a hard sphere, you get a total
scattering cross section that is 4 times bigger.
A.30.2 Partial wave amplitude
This subsection gives some further odds and ends on partial wave
analysis, for the incurably curious.
Recall that a partial wave has an asymptotic behavior
The first term corresponds to the wave function of the incoming
particles. The second term is the effect of the scattering potential.
Physicists like to write the coefficient of the scattered wave as
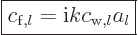 |
(A.225) |
They call the so-defined constant 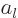 the “partial wave amplitude” because obviously it is not a partial
wave amplitude. Confusing people is always funny.
the “partial wave amplitude” because obviously it is not a partial
wave amplitude. Confusing people is always funny.
Now every partial wave by itself is a solution to the Hamiltonian
eigenvalue problem. That means that every partial wave must ensure
that particles cannot just simply disappear. That restricts what the
partial wave amplitude can be. It turns out that it can be written in
terms of a real number 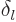 :
:
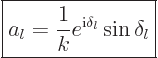 |
(A.226) |
The real number 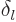 is called the “phase shift.”
is called the “phase shift.”
Some physicist must have got confused here, because it really is a
phase shift. To see that, consider the derivation of the above
result. First the asymptotic behavior of the partial wave is
rewritten in terms of exponentials using {A.6}
(A.24) and (A.25). That gives
The dots stand for common factors that are not important for the
discussion. Physically, the first term above describes spherical wave
packets that move radially inwards toward the target. The second term
describes wave packets that move radially outwards away from the
target.
Now particles cannot just disappear. Wave packets that go in towards
the target must come out again with the same amplitude. And that
means that the two terms in the asymptotic behavior above must have
the same magnitude. (This may also be shown mathematically using
procedures like in {A.32}.)
Obviously the two terms do have the same magnitude in the absence of
scattering, where 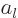 is zero. But in the presence of scattering,
the final parenthetical factor will have to stay of magnitude one.
And that means that it can be written in the form
is zero. But in the presence of scattering,
the final parenthetical factor will have to stay of magnitude one.
And that means that it can be written in the form
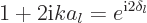 |
(A.227) |
for some real number 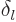 . (The factor 2 in the
exponential is put in because physicists like to think of the wave
being phase shifted twice, once on the way in to the target and once
on the way out.) Cleaning up the above expression using the Euler
formula (2.5) gives the stated result.
. (The factor 2 in the
exponential is put in because physicists like to think of the wave
being phase shifted twice, once on the way in to the target and once
on the way out.) Cleaning up the above expression using the Euler
formula (2.5) gives the stated result.
If you add in the time dependent factor 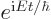 of the
complete unsteady wave function, you can see that indeed the waves are
shifted by a phase angle
of the
complete unsteady wave function, you can see that indeed the waves are
shifted by a phase angle 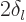 compared to the unperturbed wave
function. Without any doubt, the name of the physicist responsible
for calling the phase angle a
compared to the unperturbed wave
function. Without any doubt, the name of the physicist responsible
for calling the phase angle a phase angle
has been
ostracized from physics. She will never be heard of again.
A.30.3 The Born approximation
The Born approximation assumes that the scattering potential is weak
to derive approximate expressions for the scattering.
Consider first the case that the scattering potential is zero. In
that case, the wave function is just that of the incoming particles:
where  is the energy of the particle and
is the energy of the particle and  its mass.
its mass.
Born considered the case that the scattering potential 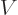 is not
zero, but small. Then the wave function
is not
zero, but small. Then the wave function 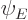 will still be close
to the incoming wave function, but no longer exactly the same. In
that case an approximation to the wave function can be obtained from
the so-called integral Schrödinger equation, {A.13}
(A.42):
will still be close
to the incoming wave function, but no longer exactly the same. In
that case an approximation to the wave function can be obtained from
the so-called integral Schrödinger equation, {A.13}
(A.42):
In particular, inside the integral the true wave function 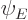 can
be replaced by the incoming wave function:
can
be replaced by the incoming wave function:
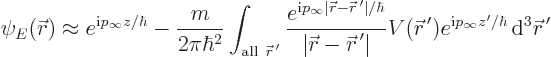 |
(A.228) |
It is not exact, but it is much better than just setting the integral
to zero. The latter would make the wave function equal to the
incoming wave. With the approximate integral, you get a valid
approximation to the particle deflections.
To get the differential cross section, examine the behavior of
(A.228) at given scattering angles  and
and  for
large
for
large  . That produces, {D.47}:
. That produces, {D.47}:
 |
(A.229) |
Here
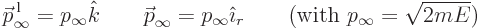 |
(A.230) |
are the classical momentum vectors of the incoming and
scattered particles. Note that the direction of 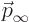 depends
on the considered scattering angles
depends
on the considered scattering angles  and
and  . And
that apparently the momentum change of the particles is a key factor
affecting the amount of scattering.
. And
that apparently the momentum change of the particles is a key factor
affecting the amount of scattering.
One additional approximation is worth mentioning. Consider particles
of such low momentum that their quantum wave length,
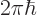

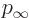 , is gigantic compared to the radial size
of the scattering potential. Particles of such wave lengths do not
notice the fine details of the scattering potential at all.
Mathematically,
, is gigantic compared to the radial size
of the scattering potential. Particles of such wave lengths do not
notice the fine details of the scattering potential at all.
Mathematically, 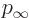 is so small that the argument of the
exponential in the differential cross section above can be assumed
zero. Then:
is so small that the argument of the
exponential in the differential cross section above can be assumed
zero. Then:
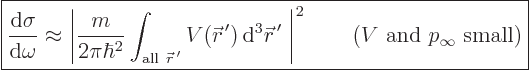 |
(A.231) |
The differential cross section no longer depends on the angular
position. If particles get scattered at all, they get scattered
equally in all directions.
Note that the integral is infinite for a Coulomb potential.
![]()
![]() -
-![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]() ,
,![]() .
.![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
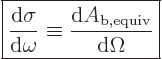
![]() :
: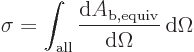
![]() :
:![]()
![]() -
-![]() ,
,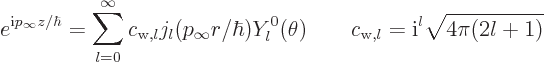
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,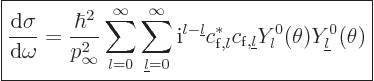
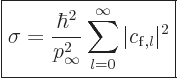
![]()
![]()
![]() ,
,![]()
![]()
![]() :
: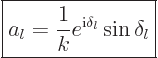
![]()
![]()
![]()
![]()
![]()
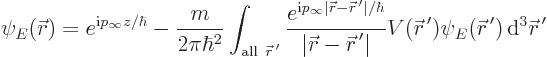
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()